Ma trận chuyển cơ sở đóng vai trò quan trọng trong đại số tuyến tính, giúp ta dễ dàng chuyển đổi giữa các hệ tọa độ khác nhau trong không gian vectơ. Nó được sử dụng rộng rãi trong nhiều lĩnh vực như hình học, giải tích vectơ, biến đổi tuyến tính,…
Ma trận chuyển cơ sở là gì?
Ma trận chuyển cơ sở là một ma trận vuông được sử dụng để chuyển đổi tọa độ của vectơ và ma trận từ hệ tọa độ này sang hệ tọa độ khác trong không gian vectơ. Nó còn được gọi là ma trận chuyển tiếp, đóng vai trò quan trọng trong đại số tuyến tính, đặc biệt là trong các lĩnh vực như hình học, giải tích vectơ, biến đổi tuyến tính và đồ họa máy tính.

Giả sử ta có hai hệ tọa độ B và C trong không gian vectơ n chiều. Ma trận cơ sở P từ hệ tọa độ B sang hệ tọa độ C được định nghĩa như sau:
- P là một ma trận vuông n x n.
- Các cột của P là các vectơ đơn vị của hệ tọa độ C biểu diễn trong hệ tọa độ B.
Cách tìm ma trận chuyển cơ sở
Để có thể tìm ma trận chuyển cơ sở chính xác nhất, bạn cần thực hiện đầy đủ các bước sau đây.
Xác định cơ sở ban đầu và cơ sở mới
Trước tiên, để tìm ma trận chuyển cơ sở từ u sang v cần xác định rõ cơ sở ban đầu (gọi là cơ sở A) và cơ sở mới (gọi là cơ sở B) mà ta muốn chuyển đổi. Đảm bảo rằng cả hai cơ sở đều là các tập hợp các vector độc lập tuyến tính và sinh ra cùng một không gian vector.
Ví dụ: Cơ sở ban đầu A = {(1,0), (0,1)} (cơ sở chuẩn), Cơ sở mới B = {(1,1), (1,-1)}
Biểu diễn các vector của cơ sở mới theo cơ sở ban đầu
Với mỗi vector trong cơ sở B, ta cần biểu diễn nó như một tổ hợp tuyến tính của các vector trong cơ sở A. Điều này thường đòi hỏi việc giải một hệ phương trình tuyến tính.
Trong trường hợp này, các vector của cơ sở B đã được biểu diễn theo cơ sở chuẩn A:
(1,1) = 1(1,0) + 1(0,1)
(1,-1) = 1(1,0) – 1(0,1)
Tạo ma trận chuyển cơ sở
Ma trận cơ sở từ A sang B được tạo bằng cách đặt các hệ số của biểu diễn tìm được ở bước 2 vào các cột của ma trận. Mỗi cột của ma trận tương ứng với một vector của cơ sở B được biểu diễn theo cơ sở A.
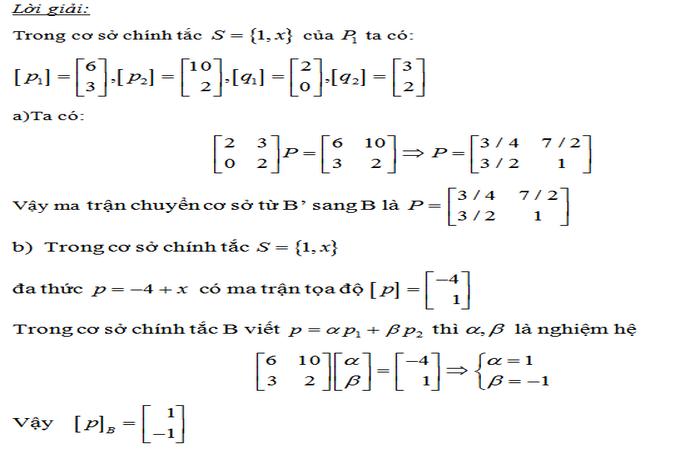
Ma trận đổi cơ sở từ A sang B được tạo bằng cách đặt các hệ số tìm được ở bước 2 vào các cột:
P = [1 1]
[1 -1]
Kiểm tra và đơn giản hóa (nếu cần)
Sau khi xây dựng ma trận, có thể cần kiểm tra lại tính đúng đắn bằng cách áp dụng nó cho một vài vector và so sánh kết quả. Nếu có thể, hãy đơn giản hóa ma trận để dễ sử dụng hơn.
Để kiểm tra, ta có thể áp dụng ma trận này cho một vector trong cơ sở A:
P * [1] = [1 1] * [1] = [2]
[0] [1 -1] [0] [1]
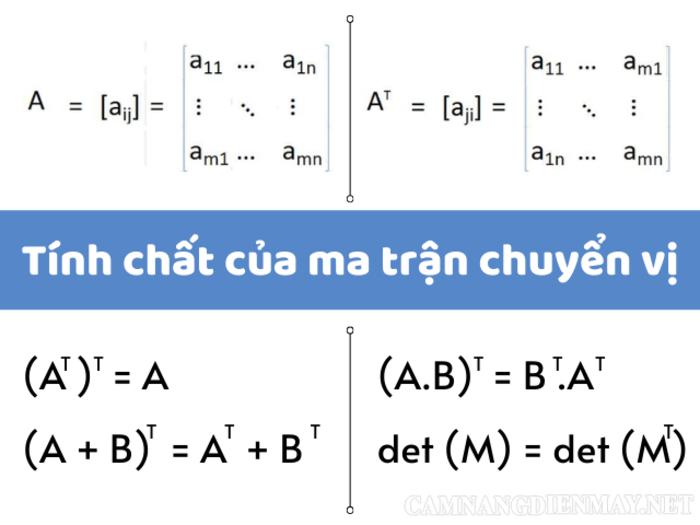
Tính chất của ma trận chuyển cơ sở
Các ma trận đổi cơ sở có một số tính chất quan trọng. Chúng tôi sẽ trình bày các tính chất chính:
Khả nghịch
Ma trận cơ sở P luôn khả nghịch vì nó biểu diễn một ánh xạ một-một giữa hai cơ sở. Điều này có nghĩa là tồn tại ma trận P^(-1) sao cho PP^(-1) = P^(-1)P = I, với I là ma trận đơn vị. Tính chất này đảm bảo rằng ta có thể chuyển đổi qua lại giữa hai cơ sở mà không mất thông tin.
Định thức khác không
Vì ma trận P khả nghịch, định thức của nó luôn khác 0: det(P) ≠ 0. Giá trị của định thức cho biết hệ số co giãn của thể tích khi chuyển đổi giữa các cơ sở.
Ma trận vuông
Trong không gian n chiều, ma trận P có kích thước n x n. Ví dụ, trong R^3, P sẽ là ma trận 3×3. Điều này phản ánh việc mỗi vector cơ sở mới được biểu diễn bằng n thành phần trong cơ sở cũ.
Tính chất nhóm
Nếu P là ma trận chuyển từ cơ sở A sang B, và Q là ma trận chuyển từ B sang C, thì PQ là ma trận chuyển từ A sang C. Phép nhân ma trận này tuân theo các quy tắc của lý thuyết nhóm, bao gồm tính kết hợp và sự tồn tại của phần tử đơn vị (ma trận đơn vị I).
Ma trận nghịch đảo
Nếu P là ma trận chuyển từ cơ sở A sang B, thì P^(-1) là ma trận chuyển từ B về A. Điều này có nghĩa là nếu v_A là vector trong cơ sở A và v_B là vector tương ứng trong cơ sở B, ta có:
v_B = Pv_A và v_A = P^(-1)v_B
Ví dụ cụ thể:
Giả sử trong R^2, ta có:
P = [2 1]
[1 1]
là ma trận từ cơ sở chuẩn sang một cơ sở mới.
Ta có thể kiểm tra:
- det(P) = 21 – 11 = 1 ≠ 0
- P^(-1) = [1 -1][-1 2]
- PP^(-1) = I = [1 0]
[0 1]
Các ứng dụng của ma trận chuyển cơ sở
Ma trận cơ sở có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khoa học khác. Dưới đây là một danh sách ngắn gọn các ứng dụng chính:
- Đơn giản hóa các phép tính trong không gian vector
- Giải quyết các bài toán hình học và biến đổi tọa độ
- Xử lý tín hiệu và hình ảnh trong công nghệ thông tin
- Phân tích dữ liệu đa chiều và giảm chiều dữ liệu
- Mô hình hóa các hệ thống động trong vật lý và kỹ thuật
- Tối ưu hóa các thuật toán trong học máy và trí tuệ nhân tạo
- Mã hóa và bảo mật thông tin
- Đồ họa máy tính và thiết kế 3D
- Phân tích cấu trúc phân tử trong hóa học và sinh học
- Xử lý ngôn ngữ tự nhiên và nhận dạng giọng nói
Lời kết
Nhìn chung, ma trận chuyển cơ sở đóng vai trò quan trọng trong toán học và đời sống. Việc hiểu rõ khái niệm, tính chất và ứng dụng của ma trận đổi cơ sở sẽ giúp ích cho học tập và nghiên cứu của bạn.




