Không gian Euclide, được đặt theo tên nhà toán học Hy Lạp cổ đại Euclid, đây là khái niệm về một mô hình toán học mô tả các thuộc tính cơ bản của hình dạng và vị trí trong không gian ba chiều. Nó đóng vai trò nền tảng cho nhiều lĩnh vực quan trọng trong toán học và vật lý, bao gồm hình học, lượng giác, cơ học và thống kê. Cùng Hoc Thế Nào tìm hiểu thêm về không gian này cũng như cách chứng minh Euclide trong bài viết dưới đây.
Định nghĩa không gian Euclide
Không gian Euclide là một không gian phẳng vô hạn, trong đó mỗi điểm được xác định bởi một tập hợp các tọa độ duy nhất. Các đặc điểm chính của không gian này bao gồm:
- Tính phẳng: Các đường thẳng trong không gian Euclid được coi là hoàn toàn thẳng và không bao giờ cong hoặc uốn lượn.
- Tính vô hạn: Không gian Euclid trải dài vô hạn theo mọi hướng, không có điểm cuối hay ranh giới.
- Tính đồng nhất: Mọi điểm trong không gian Euclid đều được coi là giống nhau và có cùng các thuộc tính.
- Hệ thống tọa độ: Vị trí của một điểm trong không gian Euclid được xác định bởi một tập hợp các tọa độ, thường là theo hệ thống Descartes với các trục x, y và z.
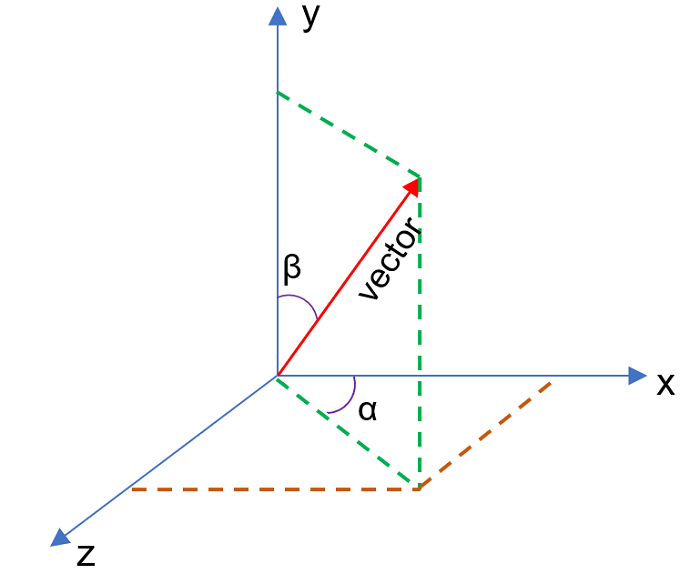
Các yếu tố hình thành
Có ba yếu tố cơ bản, hình thành nên không gian Euclid:
- Điểm: Một điểm là một vị trí cụ thể trong không gian, không có kích thước hay hình dạng.
- Đường thẳng: Đường thẳng là đường dài nhất có thể được vẽ giữa hai điểm bất kỳ. Nó được định nghĩa bởi một điểm bất kỳ trên đường thẳng và hướng của nó.
- Mặt phẳng: Mặt phẳng là một bề mặt phẳng trải dài vô hạn theo mọi hướng. Nó được tạo thành bởi vô số đường thẳng song song với nhau.
Các khái niệm quan trọng
Ngoài ba yếu tố cơ bản, bạn cần nắm vững một số khái niệm quan trọng khác như:
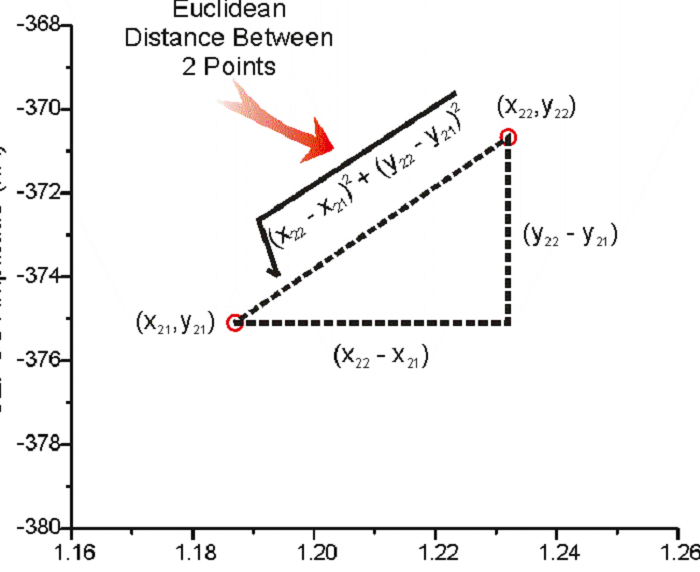
- Khoảng cách: Khoảng cách giữa hai điểm là độ dài của đoạn thẳng nối hai điểm đó được gọi là Euclidean.
- Góc: Góc là hình được tạo bởi hai đường thẳng hoặc hai mặt phẳng cắt nhau. Kích thước của góc được đo bằng đơn vị độ.
- Diện tích: Diện tích là thước đo kích thước của một mặt phẳng.
- Thể tích: Thể tích là thước đo kích thước của một vật thể ba chiều.
Ứng dụng của không gian Euclide
Không gian Euclid có vô số ứng dụng trong đời sống thực, bao gồm:
- Vật lý: Được sử dụng để mô tả chuyển động của các vật thể, lực và năng lượng.
- Kỹ thuật: Ứng dụng trong thiết kế và xây dựng các công trình, máy móc và thiết bị.
- Hàng không: Được sử dụng trong công nghệ điều hướng và định vị máy bay.
- Đồ họa máy tính: Tạo ra các hình ảnh và mô hình 3D.
- Trí tuệ nhân tạo: Không gian Euclid được sử dụng trong phát triển các hệ thống robot và xe tự lái.
Cách chứng minh không gian vectơ là không gian Euclide
Để xác định xem một không gian vector V có phải là không gian Euclid hay không, ta cần kiểm tra xem nó có thỏa mãn đồng thời hai điều kiện sau:
1. Tồn tại tích vô hướng
Không gian vectơ V cần phải có một phép toán gọi là tích vô hướng, được ký hiệu là ⟨u, v⟩, giữa hai vectơ bất kỳ u và v trong V. Tích vô hướng này phải thỏa mãn các tính chất sau:
- Tính đối xứng: ⟨u, v⟩ = ⟨v, u⟩ với mọi vectơ u và v trong V.
- Tính tích cực xác định: ⟨u, u⟩ ≥ 0 với mọi vectơ u trong V, và ⟨u, u⟩ = 0 chỉ khi u là vectơ 0.
- Tính tuyến tính theo vectơ thứ nhất: ⟨au + bv, w⟩ = a⟨u, w⟩ + b⟨v, w⟩ với mọi vectơ u, v, w trong V và mọi số thực a và b.
- Tính tuyến tính theo vectơ thứ hai (tùy chọn): ⟨u, av + bw⟩ = a⟨u, v⟩ + b⟨u, w⟩ với mọi vectơ u, v, w trong V và mọi số thực a và b.
2. Tồn tại chuẩn
Không gian vectơ V phải có một phép toán gọi là chuẩn, được ký hiệu là ||u||, trên mỗi vectơ u trong V. Chuẩn phải thỏa mãn các tính chất sau:
-
- Tính bất biến theo phép tịnh tiến: ||u + v|| = ||u|| với mọi vectơ u và v trong V.
- Tính tích cực: ||u|| ≥ 0 với mọi vectơ u trong V, và ||u|| = 0 chỉ khi u là vectơ 0.
- Tính tam giác: ||u + v|| ≤ ||u|| + ||v|| với mọi vectơ u và v trong V.
Nếu một không gian vector V thỏa mãn cả hai điều kiện trên, thì nó được gọi là không gian Euclid.
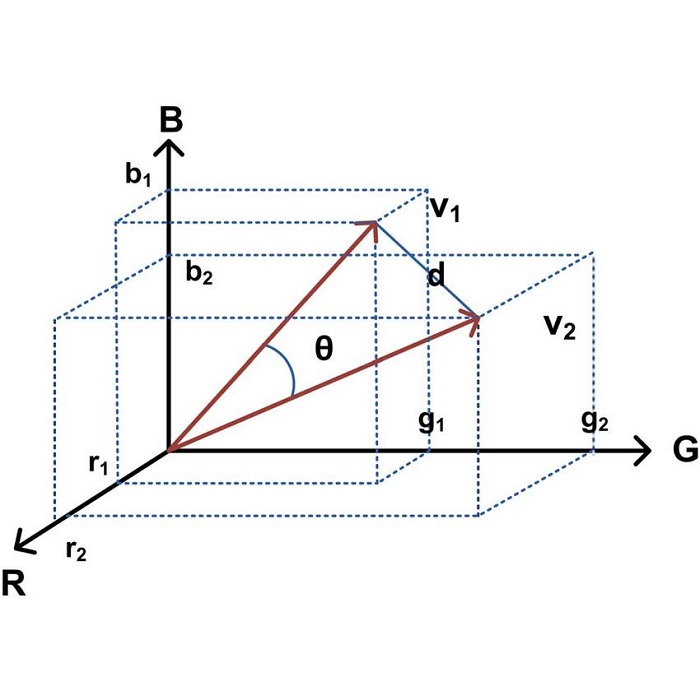
Ví dụ:
- Không gian vector R^n, với n là số nguyên dương, là một không gian Euclid.
- Không gian vector vô hạn chiều C[0, 1] của các hàm liên tục trên khoảng [0, 1] không phải là không gian Euclid vì nó không có chuẩn.
Ví dụ minh hoạ về chứng minh không gian Euclide
Dưới đây là một vài ví dụ minh hoạ về kiểm tra không gian vectơ bất kỳ có phải là không gian Euclide hay không, giúp bạn nắm vững lý thuyết và cách giải bài tập dạng này.
Ví dụ 1: Không gian vector R^2
Không gian vector R^2, bao gồm tất cả các vectơ hai chiều có dạng (x, y), với x và y là các số thực, là một không gian Euclid.
Kiểm tra:
- Tích vô hướng: Ta có thể định nghĩa tích vô hướng tiêu chuẩn trên R^2 như sau:
$$\langle(x1,\;y1),\;(x2,\;y2)\rangle\;=\;x1\;\times\;x2\;+\;y1\;\times\;y2$$
=> Tích vô hướng này thỏa mãn tất cả các tính chất của tích vô hướng Euclid.
- Chuẩn: Ta có thể định nghĩa chuẩn Euclid trên R^2 như sau:
$$\vert\vert(x,y)\vert\vert=\surd(x^2+y^2)$$
=> Chuẩn này thỏa mãn tất cả các tính chất của chuẩn Euclid.
Kết luận: Do R^2 thỏa mãn cả hai điều kiện về tích vô hướng và chuẩn Euclid, nên nó là một không gian Euclid.
Ví dụ 2: Không gian vector C[0, 1]
Không gian vector C[0, 1] bao gồm tất cả các hàm liên tục trên khoảng [0, 1].
Kiểm tra:
- Tích vô hướng: Ta có thể định nghĩa tích vô hướng tiêu chuẩn trên C[0, 1] như sau:
$$\langle f,\;g\rangle\;=\;\int\lbrack0,\;1\rbrack\;f(x)\;\times\;g(x)\;dx$$
=> Tích vô hướng này thỏa mãn tất cả các tính chất của tích vô hướng Euclid.
- Chuẩn: Tuy nhiên, không có định nghĩa chuẩn Euclid nào trên C[0, 1] thỏa mãn tất cả các tính chất của chuẩn Euclid. Ví dụ, nếu ta định nghĩa chuẩn như sau:
$$\vert\vert f\vert\vert\;=\;\int\lbrack0,\;1\rbrack\;\vert f(x)\vert\;dx$$
=> Chuẩn này không thỏa mãn tính tam giác.
Kết luận: Do C[0, 1] không có định nghĩa chuẩn Euclid nào thỏa mãn tất cả các tính chất, nên nó không phải là một không gian Euclid.
Ví dụ 3: Không gian vector L^2[0, 1]
Không gian vector L^2[0, 1] bao gồm tất cả các hàm đo được bình phương trên khoảng [0, 1].
Kiểm tra:
- Tích vô hướng: Ta có thể định nghĩa tích vô hướng tiêu chuẩn trên L^2[0, 1] như sau:
$$\langle f,\;g\rangle\;=\;\int\lbrack0,\;1\rbrack\;f(x)\;\times\;g(x)\;dx$$
=> Tích vô hướng này thỏa mãn tất cả các tính chất của tích vô hướng Euclid.
- Chuẩn: Ta có thể định nghĩa chuẩn Euclid trên L^2[0, 1] như sau:
$$\vert\vert f\vert\vert=\surd(\int\lbrack0,1\rbrack\vert f(x)\vert^2dx)$$
=> Chuẩn này thỏa mãn tất cả các tính chất của chuẩn Euclid.
Kết luận: Do L^2[0, 1] thỏa mãn cả hai điều kiện về tích vô hướng và chuẩn Euclid, nên nó là một không gian Euclid.
Lời kết
Không gian Euclide là một mô hình toán học vô cùng quan trọng, nó không chỉ được ứng dụng trong các dạng bài tập Hình học mà còn được ứng dụng rất nhiều trong đời sống thực. Nắm vững lý thuyết về phần này sẽ giúp chúng ta hiểu rõ hơn về thế giới xung quanh và có thể áp dụng kiến thức này để giải quyết mọi bài tập từ khó cho đến dễ của hình học không gian hay hình học phẳng.
Nội dung bài viết




