Hạng của ma trận là một khái niệm quan trọng trong đại số tuyến tính, đóng vai trò then chốt trong việc phân tích và giải quyết các hệ thống phương trình tuyến tính, biến đổi tuyến tính và nhiều vấn đề toán học khác. Bài viết này sẽ trả lời cụ thể câu hỏi hạng của ma trận là gì và cung cấp cho bạn một cái nhìn tổng quan về nó, bao gồm định nghĩa, tính chất và ứng dụng.
Định nghĩa hạng của ma trận
Hạng của ma trận là số chiều của không gian vectơ được sinh bởi các vectơ cột của nó. Hạng ma trận là gì đã được giải đáp, ngoài ra ta có thể hiểu là khái niệm này biểu thị số lượng vectơ cột độc lập tuyến tính tối đa của ma trận đó. Hạng của ma trận A được ký hiệu là: rank(A) hoặc rk(A).
Ma trận rỗng có đặc điểm là không có hàng hay cột nào khác 0, vì thế ma trận không có hàng hoặc cột độc lập. Do vậy mà rank ma trận rỗng bằng 0.
Lưu ý: Rank của ma trận không thể vượt quá số lượng hàng và số lượng cột của ma trận đã cho.
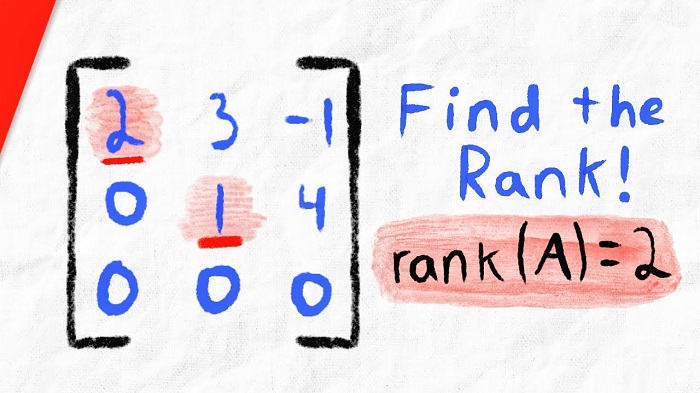
Ví dụ đơn giản về tìm hạng ma trận:
Xét ma trận A:
$$ A=\;\begin{pmatrix}1&2&-1\\3&4&-2\end{pmatrix} $$
Đầu tiên ta thực hiện biến đổi ma trận A về dạng bậc thang bằng phép biến đổi sơ cấp.
$$ A=\;\begin{pmatrix}1&2&-1\\3&4&-2\end{pmatrix} => \begin{pmatrix}1&0&1\\0&2&-1\end{pmatrix} $$
Dễ quan sát ma trận A ở dạng bậc thang, có 2 hàng khác 0.
Kết luận:
Rank ma trận A bằng 2.
Tính chất hạng ma trận
Hạng của một ma trận A bất kỳ cơ những tính chất cơ bản sau đây:
- Hạng ma trận bằng số lượng các định thức con khác 0 lớn nhất của ma trận A.
- Khi ma trận được đưa về dạng ma trận bậc thang, hạng của nó bằng số lượng các hàng khác 0 và bằng số lượng các cột khác 0 của ma trận A.
- Rank của ma trận A bằng số lượng các nghiệm độc lập của hệ phương trình tuyến tính Ax = 0.
- Với mọi vectơ b thuộc không gian vectơ sinh bởi các vectơ cột của A, hạng ma trận A bằng số lượng các nghiệm của hệ phương trình tuyến tính Ax = b.
Phương pháp tìm rank của ma trận
Có nhiều phương pháp để tìm rank của ma trận. Trong đó các phương pháp phổ biến nhất bao gồm:
- Phương pháp định thức con: Tìm định thức con lớn nhất khác 0 của ma trận A. Rank của ma trận A bằng cấp của định thức con đó.
- Phương pháp biến đổi sơ cấp: Biến đổi ma trận A về dạng bậc thang bằng các phép biến đổi sơ cấp. Rank ma trận A bằng số lượng các hàng khác 0 của ma trận A ở dạng bậc thang.
- Phương pháp Gauss-Jordan: Biến đổi ma trận A về dạng đơn vị bằng phép biến đổi Gauss-Jordan. Hạng ma trận A bằng số lượng các cột khác 0 của ma trận A ở dạng đơn vị.
Ứng dụng của tính hạng ma trận
Phương pháp tính hạng ma trận có nhiều ứng dụng trong toán học và khoa học máy tính, chẳng hạn như:
- Giải hệ phương trình tuyến tính: Rank ma trận A quyết định số lượng nghiệm của hệ phương trình tuyến tính Ax = b.
- Xác định độc lập tuyến tính: Hạng của tập vectơ được xác định bởi số lượng vectơ tối đa độc lập tuyến tính trong tập hợp đó.
- Xác định biến đổi tuyến tính: Hạng của biến đổi tuyến tính T được xác định bởi số lượng vectơ cơ sở tối đa bị biến đổi thành các vectơ độc lập tuyến tính bởi T.
- Phân tích dữ liệu: Hạng ma trận dữ liệu được sử dụng để giảm thiểu nhiễu và xác định các thành phần chính trong dữ liệu.
Bài tập về tính hạng của ma trận có lời giải
Dưới đây là phần tổng hợp một số bài tập tính hạng của ma trận giúp bạn củng cố lý thuyết và nắm được cách giải cho dạng bài này:
Bài tập 1:
Xét ma trận A:
$$ A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix} $$
Hãy tính rank ma trận A.
Lời giải:
Cách 1: Sử dụng phương pháp biến đổi sơ cấp
Biến đổi ma trận A về dạng bậc thang bằng phép biến đổi sơ cấp:
$$ A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}=>\begin{pmatrix}1&0&0\\0&1&2\\0&0&0\end{pmatrix} $$
Quan sát ma trận A ở dạng bậc thang, ta thấy nó có 2 hàng khác 0.
Kết luận: Rank của ma trận A bằng 2.
Cách 2: Cách tính hạng của ma trận bằng phương pháp định thức con
Tìm định thức con lớn nhất khác 0 của ma trận A.
$$ \begin{vmatrix}1&2\\4&5\end{vmatrix}=1 $$
Kết luận:
Rank ma trận A bằng cấp định thức con lớn nhất khác 0, tức là rank ma trận A bằng 2.
Bài tập 2:
Xét ma trận B:
$$ B=\begin{pmatrix}1&4&7\\2&5&8\\3&6&9\end{pmatrix} $$
Hãy tìm hạng của ma trận B.
Lời giải:
Cách 1: Cách tính hạng ma trận bằng phương pháp biến đổi sơ cấp
Biến đổi ma trận B về dạng bậc thang bằng phép biến đổi sơ cấp:
$$ B=\begin{pmatrix}1&4&7\\2&5&8\\3&6&9\end{pmatrix} => \begin{pmatrix}1&0&0\\0&1&1\\0&0&0\end{pmatrix} $$
Quan sát ma trận B ở dạng bậc thang, ta thấy nó có 2 hàng khác 0.
Kết luận:
Hạng ma trận B bằng 2.
Cách 2: Cách tìm hạng của ma trận bằng phương pháp định thức con
Tìm định thức con lớn nhất khác 0 của ma trận B.
$$ \begin{vmatrix}1&4\\2&5\end{vmatrix}=1 $$
Kết luận:
Rank ma trận B bằng cấp của định thức con lớn nhất khác 0, tức là rank ma trận B bằng 2.
Bài tập 3:
Cho ma trận A:
$$ A=\begin{pmatrix}1&2&m\\3&4&1\\5&6&2\end{pmatrix} $$
Tìm m để hạng ma trận bằng 3.
Lời giải:
Cách 1: Sử dụng phương pháp biến đổi sơ cấp
Biến đổi ma trận A về dạng bậc thang bằng phép biến đổi sơ cấp:
$$ A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}=>\begin{pmatrix}1&0&0\\0&2&-m+1\\0&0&0\end{pmatrix} $$
Quan sát ma trận A ở dạng bậc thang, ta thấy nó có 2 hàng khác 0.
Để rank của ma trận A bằng 3, thì hàng thứ 3 (hiện là hàng 0) cần phải có một phần tử khác 0. Do đó, ta cần có điều kiện:
-m + 1 ≠ 0
⇔ m ≠ 1
Kết luận:
Giá trị m để hạng ma trận A bằng 3 là m ≠ 1.
Cách 2: Sử dụng phương pháp định thức con
Tìm định thức con lớn nhất khác 0 của ma trận A.
$$ \begin{vmatrix}1&2\\3&4\end{vmatrix}=2 $$
Ta thấy định thức con lớn nhất khác 0 của ma trận A có cấp bằng 2. Do đó, để hạng ma trận A bằng 3, thì cần có thêm một định thức con cấp 3 khác 0.
Tuy nhiên, với giá trị m bất kỳ, ma trận A luôn có một định thức con cấp 3 bằng 0:
$$ \begin{vmatrix}1&2&m\\3&4&1\\5&6&2\end{vmatrix}=0 $$
Do đó, không có giá trị nào của m có thể khiến rank ma trận A bằng 3.
Kết luận:
Không tồn tại giá trị nào của m để rank ma trận A bằng 3.
Lời kết
Hạng của ma trận là một khái niệm quan trọng trong toán học với nhiều ứng dụng trong thực tế. Hiểu rõ về khái niệm và phương pháp giải giúp bạn giải quyết các hệ thống phương trình tuyến tính, biến đổi tuyến tính và các vấn đề toán học khác một cách dễ dàng và hiệu quả.