Chu vi hình bình hành là một khái niệm cơ bản trong toán học, giúp ta tính toán độ dài bao quanh hình. Việc nắm vững công thức này không chỉ giúp giải quyết các bài toán mà còn có ứng dụng thực tiễn trong nhiều lĩnh vực như xây dựng và thiết kế. Theo dõi bài viết dưới đây để nắm được công thức và hướng dẫn giải các bài tập ứng dụng!
Công thức tính chu vi hình bình hành
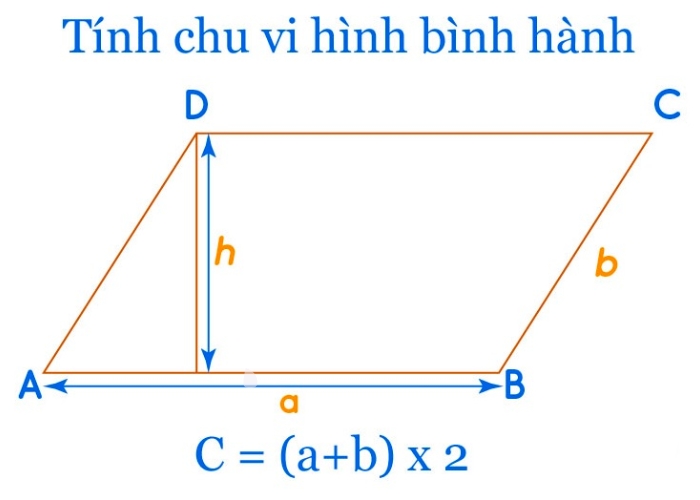
Chu vi hình bình hành được tính bằng tổng độ dài của bốn cạnh của hình bình hành, công thức tổng quát như sau:
C = 2(a + b)
Trong đó:
- C là CV hình bình hành
- a và b là độ dài hai cạnh bất kỳ của hình bình hành
Ví dụ:
Cho một hình bình hành ABCD có hai cạnh AB = 5cm và BC = 7cm. Tính cv của hình bình hành ABCD.
Áp dụng công thức, ta có:
C = 2(AB + BC) = 2(5 + 7) = 24cm
Vậy chu vi của hbh ABCD là 24cm.
Đọc ngay: Hbh là gì? Đặc điểm, dấu hiệu nhận biết và công thức tính diện tích hình bình hành
Giải thích và tính ứng dụng của công thức
Công thức tính chu vi hình bình hành C = 2(a + b) không chỉ là một công thức toán học cơ bản mà còn có nhiều ứng dụng thực tế quan trọng. Nó giúp chúng ta hiểu và tính toán chu vi của các hình bình hành trong đời sống hàng ngày, cũng như được áp dụng trong các lĩnh vực như kiến trúc, nghệ thuật, thiết kế.
- Giải thích: Công thức C = 2(a + b) xuất phát từ tính chất của hình bình hành, nơi mà các cạnh đối diện có độ dài bằng nhau. Vì vậy, chu vi của hình bình hành là tổng độ dài của cả bốn cạnh, được tính bằng hai lần tổng độ dài của một cặp cạnh kề nhau.
- Ứng dụng thực tế: Trong kiến trúc, công thức này giúp các kiến trúc sư xác định kích thước của các bức tường, cửa sổ hay các yếu tố khác có hình bình hành. Trong thiết kế, nó giúp xác định kích thước và tỉ lệ của các đối tượng để tạo ra các sản phẩm đẹp mắt, cân đối.
Ngoài ra, việc nắm vững và sử dụng thành thạo công thức này còn giúp học sinh giải quyết các bài toán hình học một cách linh hoạt, nâng cao kỹ năng giải toán cũng như khả năng tư duy logic.
Xem ngay: Cách chứng minh hình bình hành đầy đủ, chi tiết nhất
Mẹo nhớ công thức tính chu vi hình bình hành nhanh chóng
Để nhớ công thức tính cv hbh và giải bài tập một cách nhanh chóng, hãy áp dụng những mẹo sau:
- Ghi nhớ công thức cơ bản: Chu vi hbh là C = 2 x (a + b), với C là chu vi, a và b là độ dài hai cạnh kề nhau.
- Vận dụng quy tắc “nhân đôi”: Chỉ cần tính tổng độ dài của một cặp cạnh kề nhau, sau đó lấy tổng kết quả vừa tìm được nhân 2 để có chu vi.
- Thực hành qua các bài tập: Càng giải nhiều bài tập, bạn sẽ càng dễ dàng nhớ và áp dụng công thức một cách tự nhiên.
- Sử dụng các ví dụ thực tế: Liên hệ với các đồ vật xung quanh có hình dạng bình hành để hình dung và nhớ công thức tốt hơn.
Bằng cách áp dụng những mẹo trên, bạn sẽ cảm thấy dễ dàng hơn trong việc nhớ và sử dụng công thức tính chu vi hình bình hành, từ đó giúp cải thiện kỹ năng giải toán của mình.

Tham khảo ngay: Dấu hiệu nhận biết hình bình hành là gì? Có bao nhiêu cách nhận biết?
Ứng dụng chu vi hình bình hành trong thực tế
Cách tính chu vi của hình bình hành được áp dụng trong một số lĩnh vực thực tế, cụ thể:
- Xây dựng: Khi thiết kế khu đất hoặc ngôi nhà, cách tính chu vi hình bình hành giúp xác định chiều dài các đường rào xung quanh khuôn viên hoặc tính toán chiều dài của các mặt bằng trong công trình.
- Ngành điện: Trong bảng điều khiển điện, tính chu vi hbh được sử dụng để tính toán chiều dài cáp điện hoặc ống dẫn điện cần thiết cho việc dẫn dữ liệu.
- Ngành cơ khí: Trong gia công kim loại hoặc chế tạo linh kiện, công thức này giúp xã định độ dài các bộ phận hoặc đường hàn cần thiết.
- Xây dựng đường: Khi xây dựng đường, công thức cv hình bình hành giúp đo đạc và tính độ dài các đường viền, ước chừng thời gian hoàn thành công trình cũng như khối lượng vật liệu cần thiết.
- Ngành thiết kế đồ họa: Trong thiết kế đồ họa, đồ họa máy tính, công thức này được sử dụng để tạo ra hình và ảnh động chính xác về mặt hình học.

Xem thêm: Có bao nhiêu đường chéo hình bình hành? Có tính chất gì đặc biệt?
Một số dạng bài tập về chu vi hình bình hành
Khi nói đến bài tập về cv hbh, có 2 dạng bài phổ biến, thường xuyên xuất hiện nhất, cụ thể:
Dạng 1: Tính chu vi hình hành khi biết độ dài các cạnh
Phương pháp giải: Để tính cv hình bình hành, ta áp dụng công thức tính cv bằng cách nhân đôi tổng của một cặp cạnh kề nhau.
Ví dụ: Một mảnh đất hình bình hành có hai cạnh lần lượt là 30m và 50m. Hỏi cv mảnh đất hình bình hành là bao nhiêu?
Giải
Chu vi mảnh đất hbh là:
C = (30 + 50) x 2 = 80 x 2 = 160 (m)
Đáp số: 160m
Dạng 2: Cho chu vi của hình bình hành, tính độ dài các cạnh của hình đó
Phương pháp giải: Từ công thức tính cv của hình bình hành, ta có thể suy ra cách tính độ dài cạnh bất kỳ. Cụ thể:
$$C\;=\;(a\;+\;b)\;x\;2$$
$$=>\;b\;=\frac C2\;-\;a\;$$
hoặc
$$=>\;b\;=\frac C2\;-\;b$$
Ví dụ: Chu vi hbh ABCD bằng 48 cm. Tính độ dài các cạnh của hình bình hành biết độ dài cạnh AB dài hơn cạnh ngắn BD 4 cm.
Hướng dẫn giải:
Nửa chu vi của hình bình hành là:
$$\frac C2\;=\;\frac{48}2\;=\;24\;cm$$
Độ dài cạnh dài của hình bình hành là:
$$AB\;=\;\frac{24+4}2\;=\;14\;cm$$
Độ dài cạnh ngắn của hình bình hành là:
CD = 24 – 14 = 10 cm
Bài tập thực hành tại nhà
Bài 1: Cho hình bình hành ABCD có AB = 5cm, BC = 7cm. Tính chu vi của hình bình hành ABCD.
Cách giải
Áp dụng công thức tính chu vi hbh, ta có:
C = 2(AB + BC) = 2(5 + 7) = 24cm
Vậy chu vi của hbh (ABCD) là 24cm.
Bài 2: Một mảnh vườn hình bình hành có chiều dài 12m, chiều rộng 8m. Tính chu vi của mảnh vườn đó.
Cách giải
Áp dụng công thức tính chu vi HBH:
C = 2(chiều dài + chiều rộng) = 2(12 + 8) = 40m
Vậy chu vi của mảnh vườn hbh đó là 40m.
Bài 3: Cho hình bình hành ABCD có AB = 6cm, h = 4cm (h là chiều cao từ A xuống BC). Tính chu vi của hình ABCD.
Cách giải
Áp dụng công thức tính cv hình bình hành:
$$C\;=\;2h\;=\;2\;\times\;4\;=\;8cm$$
Vậy chu vi của hbh ABCD là 8cm.
Bài 4: Một hình bình hành có cạnh đáy dài 20cm, chiều cao bằng 1/2 độ dài cạnh đáy. Tính cv của hình bình hành đó.
Cách giải
Chiều cao của hình bình hành:
$$h\;=\;\frac12\;\times\;20cm\;=\;10cm$$
Áp dụng công thức tính cv hình bình hành:
$$C\;=\;2\times h\;=\;2\;\times\;10cm\;=\;20cm$$
Vậy chu vi của hình đó là 20cm.
Bài 5: Cho hình bình hành ABCD có CV là 24cm, AB = 6cm. Tính độ dài cạnh BC.
Cách giải
Gọi x là độ dài cạnh BC
Áp dụng công thức, ta có:
C = 2(AB + BC) = 24cm
=> 2(6 + x) = 24cm
=> 12 + 2x = 24cm
=> 2x = 12cm
=> x = 6cm
Vậy độ dài cạnh BC là 6cm.
Bài 6: Một mảnh đất hình bình hành có diện tích là 50m². Biết chiều cao của mảnh đất là 5m. Tính chu vi của mảnh đất đó.
Cách giải
Gọi x là độ dài cạnh đáy của mảnh đất
Diện tích mảnh đất:
$$S\;=\;x\;\times\;h\;=\;50m²\;=>\;x\;\times\;5\;=\;50m²\;=>\;x\;=\;10m$$
Chu vi mảnh đất:
$$C\;=\;2\times(x\;+\;h)\;=\;2\times(10\;+\;5)\;=\;30m$$
Vậy chu vi của mảnh đất đó là 30m.
Trên đây là chia sẻ về công thức cũng như tổng hợp những bài tập tính chu vi hình bình hành. Hy vọng bài viết đã giúp bạn hiểu rõ hơn về dạng bài này, đừng quên theo dõi các bài viết khác của Học Thế Nào để có thêm nhiều kiến thức bổ ích!