Hiểu rõ hình chữ nhật là gì và các tính chất cơ bản của nó sẽ giúp bạn dễ dàng giải quyết các bài tập toán học, cũng như áp dụng nó vào các tình huống thực tiễn. Hãy tiếp tục theo dõi bài viết để khám phá thêm nhiều ví dụ và ứng dụng thú vị liên quan đến hình chữ nhật.
Hình chữ nhật là gì?
Hình chữ nhật là một hình tứ giác có bốn góc vuông. Từ định nghĩa có thể khẳng định tứ giác lồi có bốn góc vuông hoặc hình bình hành có bốn góc vuông là hcn.
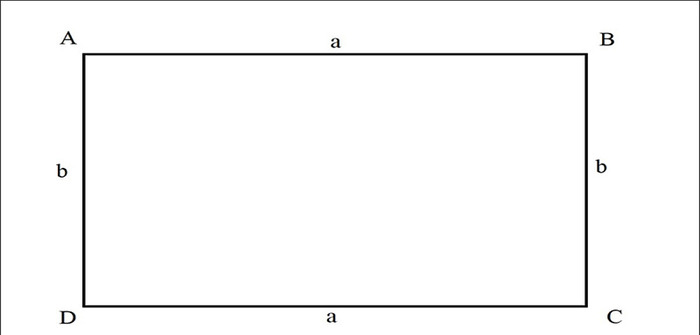
Tính chất hcn là gì?
Những tính chất của hình chữ nhật là gì? Chúng được tổng hợp qua 3 tính chất sau đây:
- Hình chữ nhật có tất cả tính chất của hình thang cân và hình bình hành, bao gồm các cặp cạnh đối song song và bằng nhau, các góc đối bằng nhau và bằng 90°.
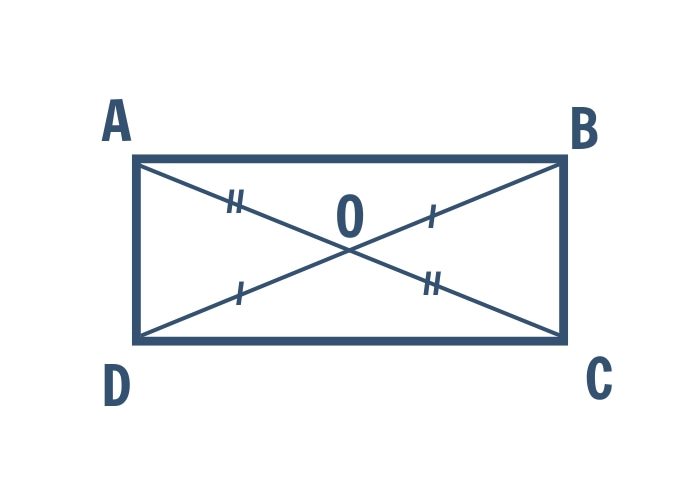
- Hai đường chéo hình chữ nhật bằng nhau, cắt nhau tại trung điểm của mỗi đường và sẽ tạo thành 4 hình tam giác cân.
- Đường tròn nội tiếp hcn có tâm là giao điểm của hai đường chéo.
Tìm hiểu 4 dấu hiệu nhận biết hình chữ nhật
Các dấu hiệu nhận biết hcn qua các định nghĩa và ví dụ dưới đây sẽ giúp bạn nắm rõ hơn về tính chất cũng như cách chứng minh:
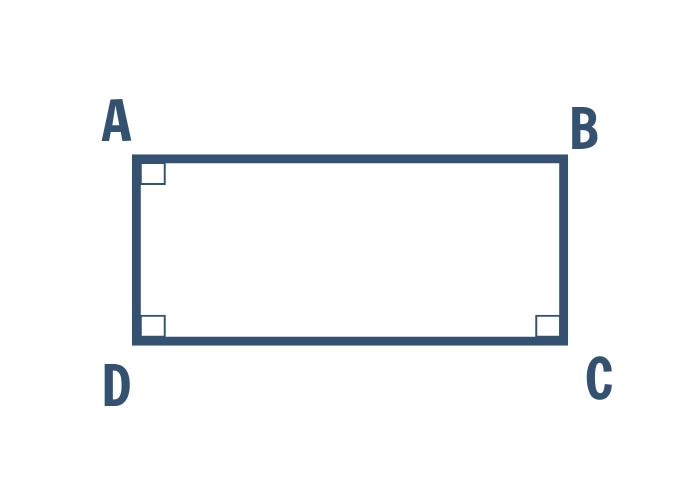
Dấu hiệu 1: Tứ giác có ba góc vuông là hình chữ nhật.
Định nghĩa: Tứ giác là hình chữ nhật nếu có ba góc trong tứ giác là góc vuông.
VD: Tứ giác ABCD có ∠A = 90°, ∠D = 90°, ∠C = 90°, CM ABCD là hình chữ nhật.
Hướng dẫn giải
Tứ giác ABCD có ∠A + ∠D + ∠C + ∠B = 360° (tổng một tứ giác = 360°).
Trong đó: 90° + 90° + 90° + ∠B = 360°
=> ∠B = 90°
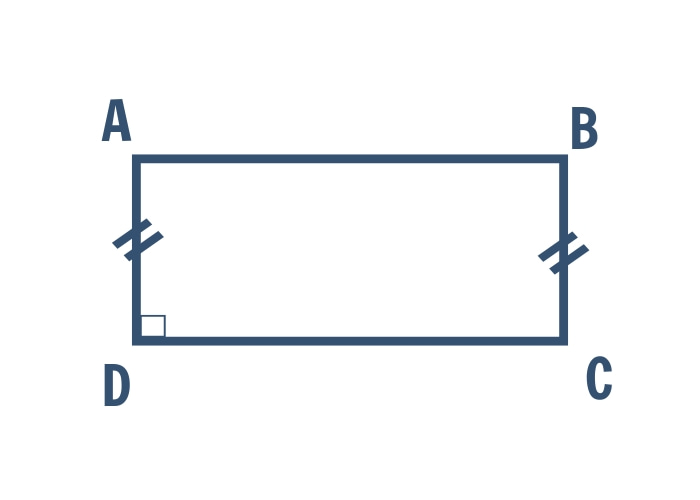
Dấu hiệu 2: Hình thang cân có một góc vuông là hình chữ nhật.
Định nghĩa: Hình thang cân là hình chữ nhật nếu có một góc trong hình thang cân là góc vuông.
VD: ABCD là hình thang cân, 2 đáy AB // CD, AD = BC, ∠D = 90°. Chứng minh ABCD là hình chữ nhật.
Hướng dẫn giải
Vì ABCD là hình thang cân, 2 góc ở đáy bằng nhau => ∠C = ∠D = 90°.
Vì ABCD là hình thang => ∠A và ∠D là 2 góc trong cùng phía bù nhau
=> ∠A + ∠D= 180°
=> ∠A +90° = 180°
=> ∠A = 90°
=> ∠A = ∠B = 90°
=> Tứ giác có 4 góc vuông nên ABCD là hình chữ nhật.
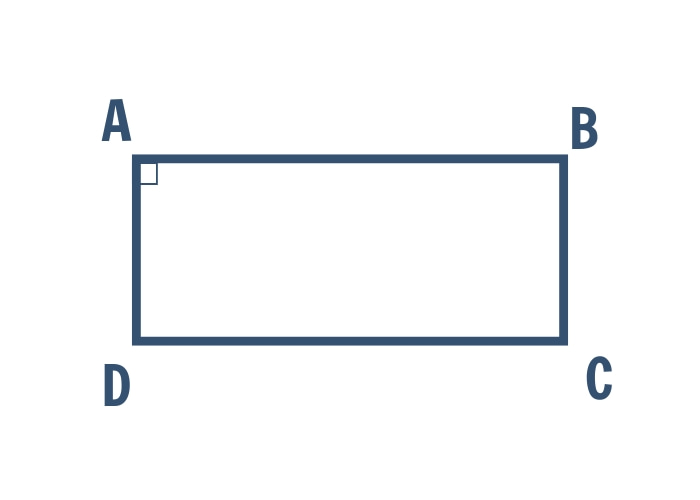
Dấu hiệu 3: Hình bình hành có một góc vuông là hình chữ nhật.
Định nghĩa: Hình bình hành là hình chữ nhật nếu có một góc trong hình bình hành là góc vuông.
VD: Cho hình bình hành có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có phải là hình chữ nhật không? Giải thích vì sao?
Hướng dẫn giải
Do ∠A = 90° và ABCD là hình bình hành nên ∠C = 90° (hai góc đối của hình bình hành)
∠D = 90° do ∠A +∠D = 180°
∠B = 90° do ∠A +∠B = 180°
Dấu hiệu 4: Hình bình hành có hai đường chéo bằng nhau cũng là hình chữ nhật.
Định nghĩa: Hình bình hành là hình chữ nhật nếu hai đường chéo của nó bằng nhau.
VD: Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
Hướng dẫn giải
O là trung điểm của AC, BD (AC = BD, OA = OC, OB = OD) nên ABCD là hình chữ nhật.
Công thức tính diện tích và chu vi hình chữ nhật
Công thức tính chu vi
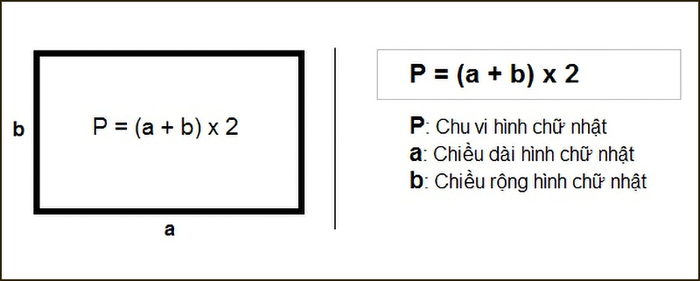
Chu vi hình chữ nhật bằng tổng độ dài của các cạnh. Công thức tính chu vi sẽ bằng chiều dài cộng chiều rộng rồi nhân 2.
Công thức như sau:
P = (a+b)x2
Trong đó P là chu vi, a là chiều dài, b là chiều rộng của hình chữ nhật.
Công thức tính diện tích
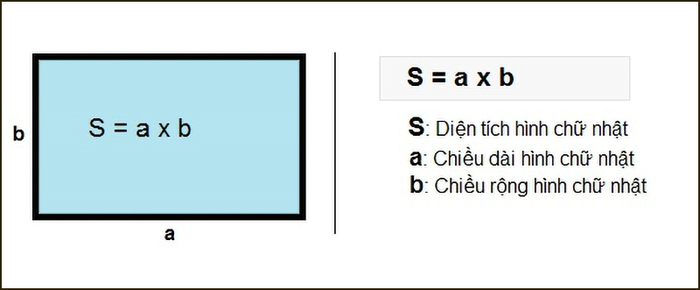
Diện tích hình chữ nhật bằng phần mặt phẳng giới hạn bởi các cạnh của hình và tính bằng công thức chiều dài nhân với chiều rộng.
Công thức:
S = axb
Trong đó S là diện tích, a là chiều dài, b là chiều rộng hình chữ nhật.
Ứng dụng của hình chữ nhật trong thực tế
Hình chữ nhật là dạng hình học cơ bản và được ứng dụng phổ biến trong cuộc sống. Một số ví dụ thường gặp nhất về ứng dụng hình chữ nhật có thể kể đến như sau:
- Kiến trúc và xây dựng: Ứng dụng của hcn sử dụng trong thiết kế các tòa nhà, phòng, cửa,… Đây là hình dáng cơ sở để tạo nên các loại kiến trúc khác nhau.
- Thiết kế đồ hoạ và nghệ thuật: Hình chữ nhật ứng dụng để tạo nên các layout, poster, banner,… hay những yếu tố trực quan khác. Trong nghệ thuật trừu tượng, đây cũng là một dạng hình cơ bản.
- Khoa học và công nghệ: Những loại màn hình hiển thị thường được thiết kế là hình chữ nhật. Đồng thời các mô phỏng, mô hình hoá khoa học cũng được ứng dụng loại hình này.
- Đóng gói và vận chuyển: Hcn là dạng hình phổ biến nhất được ứng dụng để tạo nên các loại hộp đựng sản phẩm để tăng không gian lưu trữ và dễ dàng vận chuyển.
Ngoài ra còn có rất nhiều ứng dụng khác của hcn được ứng dụng trong cuộc sống thường ngày.
Một số bài toán liên quan đến hình chữ nhật
Ví dụ 1: Tính chu vi, diện tích hình chữ nhật có:
a, chiều dài 12 cm, chiều rộng 8 cm.
b, chiều dài 30 dm, chiều rộng 20 dm
c, chiều dài 25 cm, chiều rộng 17 cm
d, chiều dài 3dm5cm, chiều rộng 11cm
Lời giải
a, Chu vi hình chữ nhật: (12 + 8) x 2 = 40 (cm)
Diện tích hình chữ nhật: 12 x 8 = (cm²)
b, Chu vi hình chữ nhật: (30 + 20) x 2 = 100 (dm)
Diện tích hình chữ nhật: 30 x 20 = 600 (dm²)
c, Chu vi hình chữ nhật: (25 + 17) x 2 = 84 (cm)
Diện tích hình chữ nhật: 25 x 17 = (cm²)
d, Đổi 3dm5cm = 35 cm
Chu vi hình chữ nhật: (35 + 11) x 2 = 92 (cm)
Diện tích hình chữ nhật: 35 x 11 = 385 (cm²)
Ví dụ 2: Một mảnh vườn hình chữ nhật với chiều rộng là 20m, chiều dài gấp 2 lần chiều rộng. Nếu muốn làm một hàng rào xung quanh khu vườn đó (có hai cửa ra vào, mỗi cửa rộng 2,5m) thì cần làm hàng rào bao nhiêu mét.
Lời giải
Theo đề bài ta có, chiều dài hình chữ nhật là: 20 x 2 = 40 (m)
Chu vi của mảnh vườn là: (20 + 40) x 2 = 120 (m)
Chiều dài hàng rào được tính bằng chu vi của vườn trừ đi phần chiều dài của cửa. Như vậy hàng rào cần làm có chiều dài là:
120 – 2,5 x 2 = 115 (m)
Các bài tập thực hành về hình chữ nhật bao gồm lời giải cụ thể
Không chỉ quan trọng trong lý thuyết mà những bài tập ứng dụng về hình chữ nhật cũng góp phần giúp học sinh hay mọi người có thể cải thiện được kỹ năng giải toán. Chúng tôi cung cấp một số dạng bài tập vận dụng bao gồm lời giải chi tiết dưới đây:
- Bài tập 1: Cho hình chữ nhật ABCD với chiều dài AB là 8cm và chiều rộng BC là 6cm. Tính diện tích và chu vi của hình chữ nhật đó.
- Bài tập 2: Một tứ giác ABCD có AB = CD, BC = DA và ∠𝐴=∠𝐶=90. Chứng minh rằng ABCD là hình chữ nhật.
- Bài tập 3: Tính độ dài đường chéo của hình chữ nhật với chiều dài là 10cm và chiều rộng là 6cm.
Lời giải
Bài tập 1: Tính diện tích và chu vi của hình chữ nhật ABCD

Bài tập 2: Chứng minh tứ giác ABCD là hình chữ nhật

Bài tập 3: Tính độ dài đường chéo của hình chữ nhật

Lời kết
Trên đây là những thông tin giải đáp về hình chữ nhật là gì cùng những dhnb hình chữ nhật và bài tập liên quan. Bài viết đã cung cấp được kiến thức bổ ích, giúp bạn đọc có thể vận dụng vào cuộc sống. Nếu có góp ý hay phản hồi, đừng ngại bình luận ngay bên dưới nhé!
Nội dung bài viết
- 1. Hình chữ nhật là gì?
- 2. Tính chất hcn là gì?
- 3. Tìm hiểu 4 dấu hiệu nhận biết hình chữ nhật
- 4. Công thức tính diện tích và chu vi hình chữ nhật
- 5. Ứng dụng của hình chữ nhật trong thực tế
- 6. Một số bài toán liên quan đến hình chữ nhật
- 7. Các bài tập thực hành về hình chữ nhật bao gồm lời giải cụ thể
- 8. Lời kết Bài tập 3: Tính độ dài đường chéo của hình chữ nhậtBài tập 3: Tính độ dài đường chéo của hình chữ nhậtBài tập 3: Tính độ dài đường chéo của hình chữ nhậtBài tập 3: Tính độ dài đường chéo của hình chữ nhậtBài tập 3: Tính độ dài đường chéo của hình chữ nhậtBài tập 3: Tính độ dài đường chéo của hình chữ nhậtd \approx 11.66 \, \text{cm}




