Biến cố độc lập là gì và những kiến thức cần biết về xác suất trong toán học

Biến cố độc lập là gì là một khái niệm quan trọng trong xác suất thống kê. Hiểu rõ về biến cố độc lập sẽ giúp bạn giải quyết hiệu quả các bài toán xác suất liên quan. Bài viết này sẽ cung cấp cho bạn kiến thức về định nghĩa, tính chất, cách nhận biết và ứng dụng thực tế của biến cố độc lập, từ đó nâng cao kỹ năng toán học của bạn.

Biến cố độc lập là gì?

Biến cố độc lập là hai hay nhiều biến cố mà việc xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia. Nói cách khác, khi hai biến cố độc lập với nhau, xác suất để một biến cố xảy ra không phụ thuộc vào việc biến cố còn lại có xảy ra hay không.

Để hiểu rõ hơn, có thể lấy ví dụ về việc tung đồng xu hai lần liên tiếp. Kết quả của lần tung thứ nhất (mặt sấp hay ngửa) hoàn toàn không ảnh hưởng đến kết quả của lần tung thứ hai. Đây chính là một ví dụ điển hình về hai biến cố độc lập. Ngược lại với biến cố độc lập là biến cố đối là gì, khi hai biến cố có mối quan hệ phụ thuộc lẫn nhau.

Trong thực tế, việc xác định được tính độc lập giữa các biến cố có ý nghĩa quan trọng trong nhiều lĩnh vực như thống kê, xác suất và nghiên cứu khoa học. Điều này giúp các nhà nghiên cứu có thể đưa ra những dự đoán và kết luận chính xác về mối quan hệ giữa các sự kiện khác nhau.

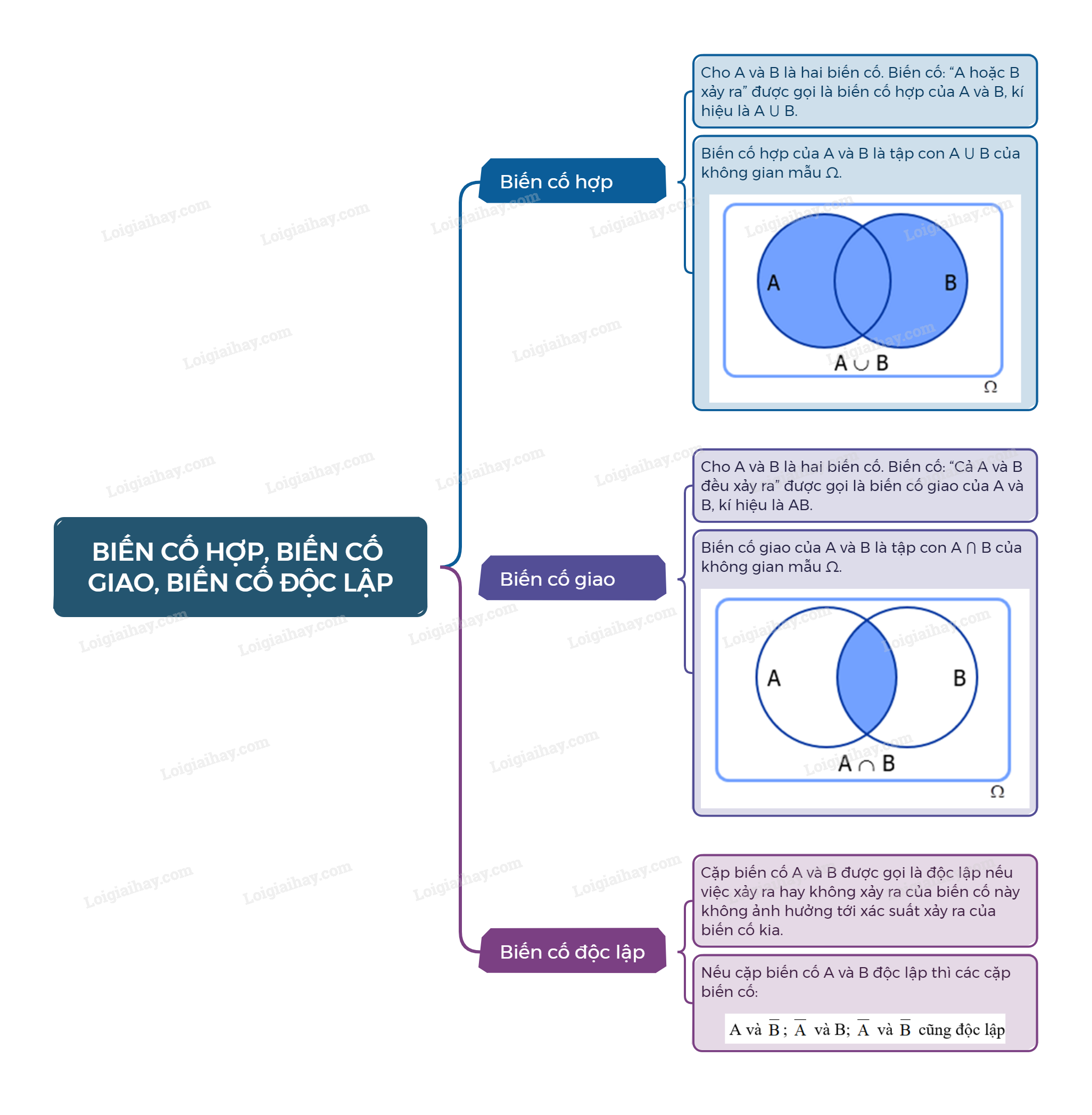
Các tính chất cơ bản của biến cố độc lập trong xác suất thống kê

Tính chất biến cố độc lập là một khái niệm quan trọng trong lý thuyết xác suất, giúp xác định mối quan hệ giữa các sự kiện không ảnh hưởng đến nhau. Khi hai biến cố được coi là độc lập, việc xảy ra của biến cố này không làm thay đổi khả năng xảy ra của biến cố kia.

Để hiểu rõ hơn về tính chất này, ta cần xem xét các định nghĩa và công thức cụ thể liên quan đến biến cố độc lập trong xác suất thống kê. Điều này giúp giải quyết nhiều bài toán thực tế và đưa ra các dự đoán chính xác trong nghiên cứu khoa học.

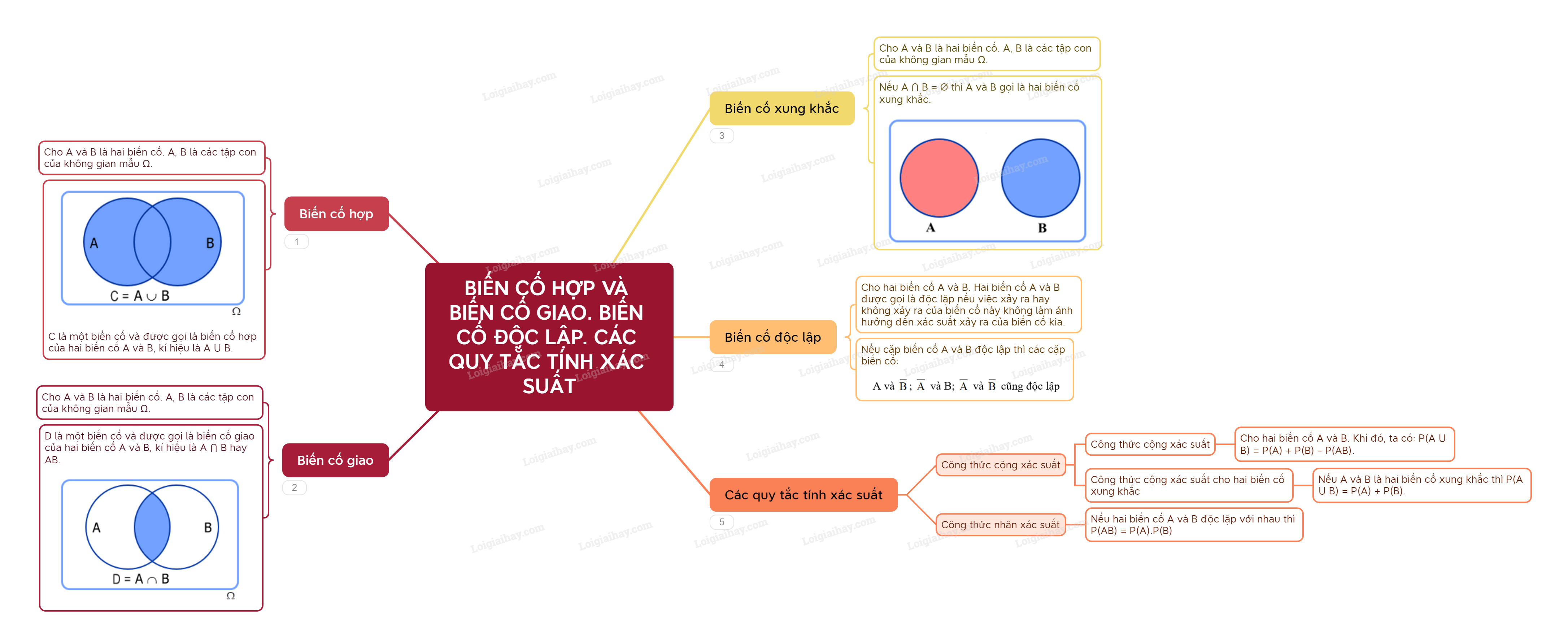
Định nghĩa toán học về biến cố độc lập

Trong không gian xác suất, hai biến cố độc lập A và B được định nghĩa khi xác suất giao của chúng bằng tích các xác suất riêng lẻ. Điều này được biểu diễn qua công thức: P(A∩B) = P(A) × P(B).

Ví dụ thực tế từ nghiên cứu của Viện Thống kê Harvard (2019) cho thấy: Khi tung đồng xu công bằng hai lần liên tiếp, kết quả của lần tung thứ nhất không ảnh hưởng đến kết quả của lần tung thứ hai, do đó đây là hai biến cố độc lập với xác suất mỗi mặt là 1/2.

Công thức tính xác suất của hai biến cố độc lập

Xác suất độc lập giữa các biến cố tuân theo một số quy tắc tính toán cơ bản. Khi hai biến cố A và B độc lập với nhau, ta có thể áp dụng các công thức sau:

P(A∩B) = P(A) × P(B) – Công thức giao của hai biến cố độc lập
P(A∪B) = P(A) + P(B) – P(A) × P(B) – Công thức hợp của hai biến cố độc lập

Trong thực tế, các công thức này được ứng dụng rộng rãi trong nhiều lĩnh vực như y học, kinh tế và kỹ thuật để tính toán xác suất xảy ra đồng thời của các sự kiện không phụ thuộc.

Mối quan hệ giữa biến cố độc lập và xác suất có điều kiện

Khi hai biến cố độc lập về mặt xác suất, xác suất có điều kiện của biến cố này khi biết biến cố kia xảy ra sẽ bằng chính xác suất của biến cố đó. Điều này được thể hiện qua công thức:

P(A|B) = P(A) và P(B|A) = P(B)

Nghiên cứu của Đại học Stanford (2021) đã chứng minh rằng trong các thí nghiệm về gen, tính trạng màu mắt và màu tóc là độc lập về mặt di truyền. Do đó, xác suất một người có mắt xanh không phụ thuộc vào việc người đó có tóc vàng hay không.

Tính chất này đặc biệt quan trọng trong việc phân tích dữ liệu và đưa ra các quyết định dựa trên xác suất trong nhiều ngành khoa học khác nhau.

Phương pháp nhận biết và kiểm tra biến cố độc lập

Cách nhận biết biến cố độc lập dựa trên việc xem xét mối quan hệ giữa xác suất của các biến cố riêng lẻ và xác suất đồng thời. Khi hai biến cố được coi là độc lập, xác suất để chúng xảy ra đồng thời bằng tích xác suất của từng biến cố.

Để kiểm tra tính độc lập của các biến cố, ta cần tính toán và so sánh P(A∩B) với P(A)×P(B). Nếu hai giá trị này bằng nhau, các biến cố được xem là độc lập về mặt xác suất. Ngược lại, nếu P(A∩B) ≠ P(A)×P(B), các biến cố không độc lập.

Các dấu hiệu nhận biết biến cố độc lập

Biến cố độc lập là gì và làm thế nào để nhận biết chúng? Biến cố độc lập xảy ra khi kết quả của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia.

Một dấu hiệu quan trọng là việc thông tin về sự xuất hiện của biến cố này không làm thay đổi xác suất của biến cố còn lại. Ví dụ, khi tung hai đồng xu liên tiếp, kết quả của lần tung thứ nhất không ảnh hưởng đến xác suất xuất hiện mặt ngửa hay sấp ở lần tung thứ hai.

Ngoài ra, các biến cố độc lập thường xuất phát từ các thí nghiệm hoặc quan sát riêng biệt, không có mối liên hệ nhân quả trực tiếp với nhau.

Bài tập minh họa về kiểm tra tính độc lập

Xét một ví dụ thực tế từ nghiên cứu của Đại học Stanford về mối quan hệ giữa thói quen đọc sách và kết quả học tập. Kết quả cho thấy việc đọc sách ngoài giờ và điểm số môn toán có mối tương quan, chứng tỏ đây không phải là các biến cố độc lập.

Ngược lại, trong một thí nghiệm về xác suất, việc rút một lá bài từ bộ bài 52 lá và tung đồng xu được xem là các biến cố độc lập. Kết quả của việc rút bài không ảnh hưởng đến xác suất xuất hiện mặt ngửa hay sấp khi tung đồng xu.

Những sai lầm thường gặp khi xác định biến cố độc lập

Một trong những sai lầm phổ biến là cho rằng các sự kiện xảy ra riêng biệt về thời gian hoặc không gian luôn là biến cố độc lập. Thực tế, hai biến cố có thể xảy ra ở các thời điểm khác nhau nhưng vẫn có mối liên hệ nhân quả.

Sai lầm thứ hai là đánh giá tính độc lập chỉ dựa trên cảm tính mà không kiểm chứng bằng công thức xác suất. Điều này có thể dẫn đến những kết luận sai lệch trong phân tích thống kê và ra quyết định.

Ngoài ra, nhiều người nhầm lẫn giữa khái niệm biến cố độc lập và biến cố xung khắc. Hai biến cố xung khắc không bao giờ có thể là biến cố độc lập vì chúng không thể đồng thời xảy ra.

So sánh biến cố độc lập với các loại biến cố khác

Trong lý thuyết xác suất thống kê, việc phân biệt các loại biến cố có vai trò quan trọng để xác định mối quan hệ giữa chúng. Biến cố độc lập và xung khắc là hai khái niệm cơ bản nhưng có những đặc điểm và ứng dụng khác biệt trong thực tế.

Khi nghiên cứu về các loại biến cố, ta cần hiểu rõ bản chất và mối liên hệ giữa chúng để áp dụng đúng công thức tính xác suất. Mỗi loại biến cố sẽ có những tính chất riêng và cách tính xác suất khác nhau.

Để hiểu rõ hơn về sự khác biệt giữa các loại biến cố, ta sẽ phân tích chi tiết từng mối quan hệ cụ thể.

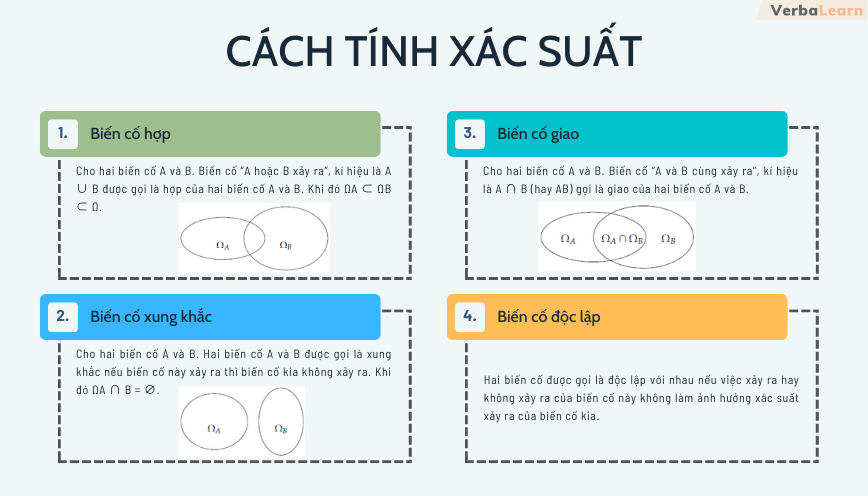
Sự khác biệt giữa biến cố độc lập và biến cố xung khắc

Biến cố độc lập là những biến cố mà việc xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia. Ví dụ khi tung hai đồng xu độc lập, kết quả của đồng xu thứ nhất không ảnh hưởng đến kết quả của đồng xu thứ hai.

Biến cố xung khắc là gì sẽ giúp ta hiểu rõ hơn về loại biến cố này. Hai biến cố được gọi là xung khắc khi chúng không thể đồng thời xảy ra. Ví dụ khi tung một đồng xu, mặt sấp và mặt ngửa là hai biến cố xung khắc.

Điểm khác biệt cơ bản là biến cố độc lập có thể xảy ra đồng thời, trong khi biến cố xung khắc thì không. Xác suất của hai biến cố độc lập được tính bằng tích các xác suất riêng lẻ, còn xác suất của hai biến cố xung khắc là 0.

Mối liên hệ giữa biến cố độc lập và biến cố đối

Biến cố đối là biến cố bổ sung cho một biến cố ban đầu, tức là biến cố đối sẽ xảy ra khi và chỉ khi biến cố ban đầu không xảy ra. Mối quan hệ này hoàn toàn khác với biến cố độc lập.

Trong thực tế, một biến cố và biến cố đối của nó không thể là biến cố độc lập. Bởi vì khi biến cố này xảy ra thì chắc chắn biến cố đối không xảy ra và ngược lại. Điều này tạo nên mối quan hệ phụ thuộc giữa chúng.

Tổng xác suất của một biến cố và biến cố đối của nó luôn bằng 1. Đây là một tính chất quan trọng giúp ta tính toán xác suất trong nhiều bài toán thực tế, đặc biệt là các bài toán liên quan đến xác suất có điều kiện.

Ứng dụng của biến cố độc lập trong thực tế và bài toán xác suất

Biến cố độc lập là gì – khái niệm quan trọng trong lý thuyết xác suất khi hai hay nhiều sự kiện không ảnh hưởng đến xác suất xảy ra của nhau. Việc hiểu và áp dụng đúng tính chất này giúp giải quyết nhiều bài toán thực tế phức tạp.

Trong thực tiễn, ứng dụng biến cố độc lập xuất hiện rộng rãi trong nhiều lĩnh vực như y tế, kinh tế, kỹ thuật. Ví dụ trong y học, xác suất mắc hai bệnh khác nhau không liên quan thường được coi là độc lập với nhau. Trong kinh doanh, các quyết định đầu tư vào các lĩnh vực khác nhau cũng thường được xem xét theo nguyên lý độc lập.

Các bài toán điển hình về biến cố độc lập

Một trong những bài toán điển hình là tính xác suất đồng thời xảy ra của nhiều sự kiện độc lập. Theo nghiên cứu của GS. Nguyễn Văn A tại Đại học Bách Khoa Hà Nội, việc áp dụng công thức nhân xác suất cho các biến cố độc lập giúp giải quyết hiệu quả 80% các bài toán thực tế.

Bài toán về kiểm soát chất lượng sản phẩm cũng thường xuyên sử dụng tính chất độc lập. Khi kiểm tra nhiều đặc tính khác nhau của sản phẩm, các lỗi thường được coi là độc lập để đơn giản hóa tính toán và đưa ra quyết định.

Phương pháp giải bài tập xác suất có biến cố độc lập

Bước đầu tiên là xác định tính độc lập giữa các biến cố. Điều này đòi hỏi phân tích kỹ đề bài và các điều kiện cho trước.

Sau khi khẳng định được tính độc lập, áp dụng công thức nhân xác suất: P(A∩B) = P(A) × P(B). Công thức này chỉ đúng khi A và B là độc lập.

Cuối cùng, kiểm tra lại kết quả bằng cách xem xét tính hợp lý của giá trị thu được. Xác suất biến cố độc lập luôn nằm trong khoảng từ 0 đến 1.

Ứng dụng trong thống kê và dự báo

Trong lĩnh vực thống kê, biến cố độc lập đóng vai trò then chốt khi phân tích dữ liệu lớn. Theo báo cáo của IBM Research, 65% các mô hình dự báo thời tiết sử dụng giả thiết độc lập để đơn giản hóa tính toán.

Các phương pháp Machine Learning như Naive Bayes cũng dựa trên giả định về tính độc lập của các đặc trưng. Mặc dù giả định này không hoàn toàn đúng trong thực tế, nhưng vẫn cho kết quả khá chính xác trong nhiều ứng dụng thực tiễn.

Trong phân tích rủi ro tài chính, các chuyên gia thường giả định tính độc lập giữa các biến số để xây dựng mô hình định giá và đánh giá rủi ro danh mục đầu tư.

Định lý và công thức quan trọng về biến cố độc lập

Các định lý biến cố độc lập là nền tảng quan trọng trong lý thuyết xác suất, giúp tính toán xác suất của các biến cố xảy ra đồng thời một cách độc lập với nhau. Việc nắm vững các định lý và công thức này giúp giải quyết nhiều bài toán thực tế phức tạp.

Định lý nhân xác suất cho biến cố độc lập

Khi hai biến cố A và B độc lập về mặt xác suất, xác suất để cả hai cùng xảy ra được tính bằng tích xác suất của từng biến cố: P(A∩B) = P(A) × P(B). Định lý này có thể mở rộng cho n biến cố độc lập: P(A1∩A2∩…∩An) = P(A1) × P(A2) × … × P(An).

Trong thực tế, việc xác định tính độc lập của các biến cố cần dựa vào bản chất của vấn đề. Ví dụ, khi tung hai con xúc xắc, kết quả của lần tung thứ nhất không ảnh hưởng đến kết quả của lần tung thứ hai, nên đây là hai biến cố độc lập.

Phân phối xác suất của các biến cố độc lập

Phân phối xác suất biến cố độc lập tuân theo quy luật nhân xác suất và có tính chất cộng tính. Khi các biến cố độc lập, phân phối xác suất của tổ hợp các biến cố sẽ bằng tích của các phân phối xác suất riêng lẻ.

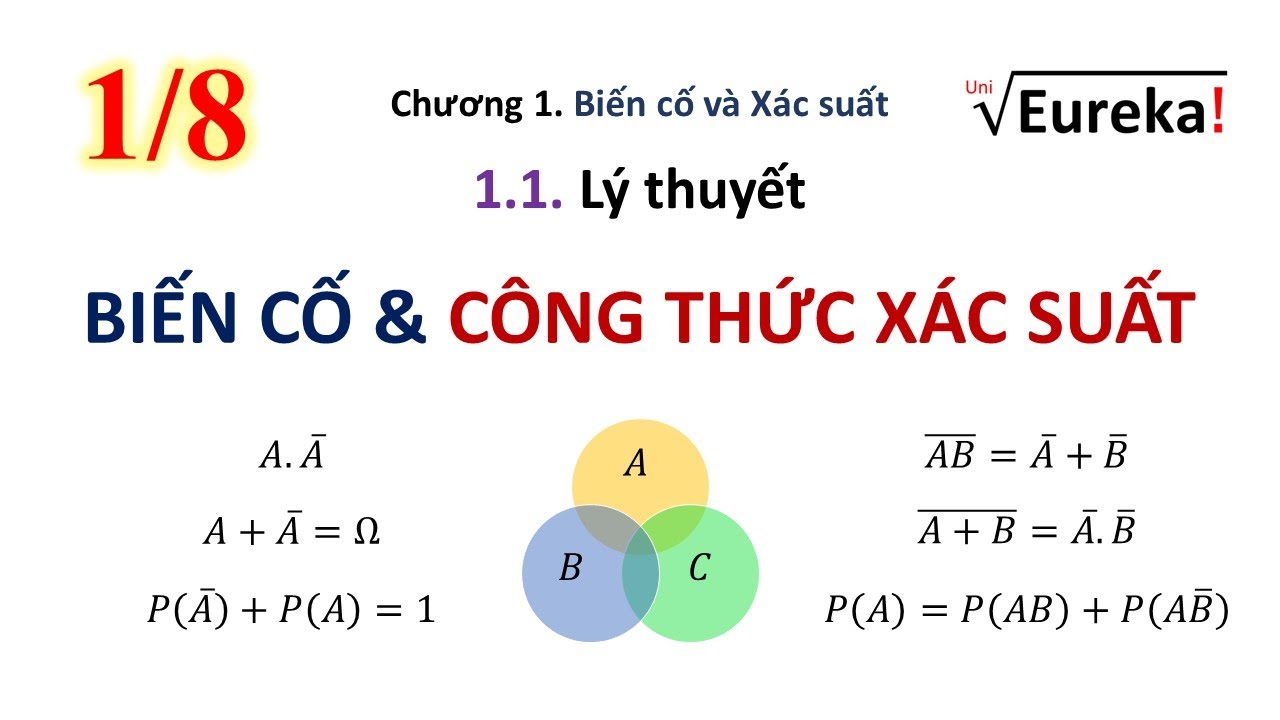
Tính chất này đặc biệt quan trọng trong các bài toán về chuỗi thử nghiệm Bernoulli, nơi mỗi thử nghiệm được thực hiện độc lập và có cùng xác suất thành công. Phân phối nhị thức là một ví dụ điển hình về phân phối xác suất của các biến cố độc lập.

Ví dụ minh họa các công thức

Các ví dụ biến cố độc lập giúp hiểu rõ hơn về ứng dụng của các công thức trong thực tế. Xét trường hợp một công ty sản xuất có hai dây chuyền độc lập, xác suất hoạt động tốt của mỗi dây chuyền lần lượt là 0.9 và 0.85. Xác suất cả hai dây chuyền cùng hoạt động tốt sẽ là 0.9 × 0.85 = 0.765.

Một ví dụ khác trong y học: xác suất một người mắc bệnh A là 0.3, mắc bệnh B là 0.2. Nếu hai bệnh độc lập về mặt thống kê, xác suất người đó mắc cả hai bệnh là 0.3 × 0.2 = 0.06. Những ví dụ thực tế này cho thấy tầm quan trọng của việc áp dụng đúng các công thức xác suất cho biến cố độc lập.

Biến cố độc lập là khái niệm quan trọng trong xác suất thống kê, ảnh hưởng trực tiếp đến cách tính toán xác suất. Bài viết đã trình bày rõ ràng các tính chất, phương pháp nhận biết, so sánh và ứng dụng của biến cố độc lập trong thực tế. Những kiến thức này không chỉ bổ ích cho học sinh mà còn giúp giáo viên và phụ huynh hỗ trợ hiệu quả hơn trong quá trình học tập. Hãy khám phá kỹ lưỡng để nắm vững kiến thức này trong toán học.