Khái niệm và ứng dụng biểu đồ Venn trong toán học và logic dễ hiểu

Biểu đồ Venn là gì? Đây là công cụ hữu ích trong toán học, giúp người học hiểu rõ mối quan hệ giữa các tập hợp. Thông qua các hình tròn giao nhau, biểu đồ này không chỉ hỗ trợ phân tích dữ liệu mà còn nâng cao tư duy logic. Hãy cùng khám phá những ứng dụng và cách sử dụng biểu đồ Venn hiệu quả trong học tập.

Biểu đồ venn là gì?

Biểu đồ venn là gì – một công cụ trực quan dùng để thể hiện mối quan hệ logic giữa các tập hợp thông qua các hình tròn chồng lấn lên nhau. Mỗi hình tròn đại diện cho một tập hợp, phần giao nhau giữa các hình tròn thể hiện các phần tử chung giữa các tập hợp đó. Đây là phương pháp được phát triển bởi nhà toán học John Venn vào năm 1880.

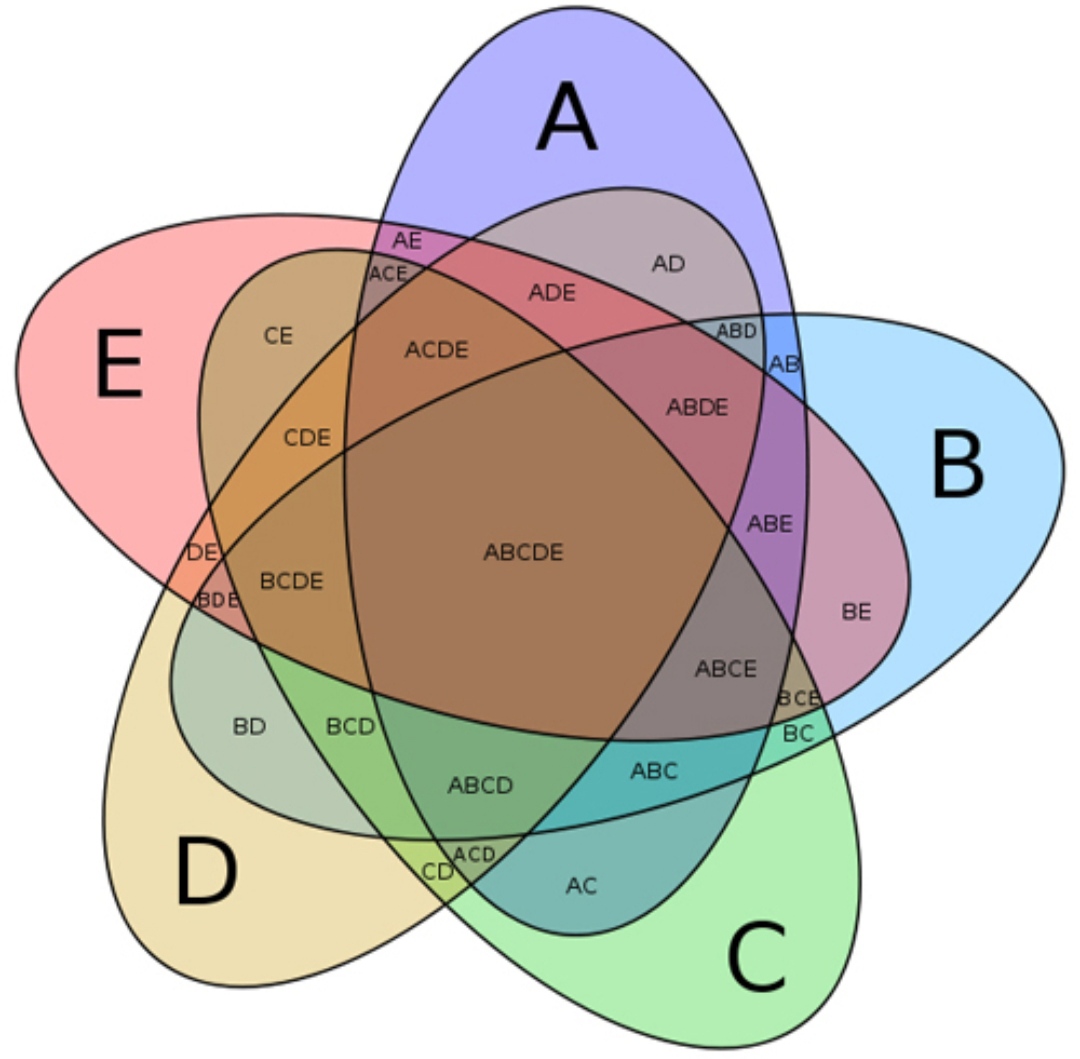
Khi tìm hiểu về sơ đồ venn là gì, ta có thể thấy đây là công cụ rất hữu ích trong việc phân tích dữ liệu và giải quyết các bài toán logic. Theo Học Thế Nào, việc sử dụng biểu đồ Venn giúp người học dễ dàng nắm bắt các khái niệm trừu tượng và mối liên hệ giữa chúng thông qua hình ảnh trực quan.

Venn diagram là gì – thuật ngữ tiếng Anh chỉ biểu đồ Venn – được ứng dụng rộng rãi trong nhiều lĩnh vực như toán học, thống kê, marketing và khoa học máy tính. Biểu đồ này đặc biệt hiệu quả trong việc so sánh và đối chiếu các đặc điểm, tìm ra điểm chung và khác biệt giữa các nhóm đối tượng, từ đó đưa ra các quyết định phù hợp trong nghiên cứu và phân tích.

Cấu trúc và thành phần cơ bản của biểu đồ Venn

Biểu đồ Venn là gì? Đây là một sơ đồ hình học sử dụng các hình tròn giao nhau để thể hiện mối quan hệ logic giữa các tập hợp. Được phát triển bởi nhà toán học John Venn vào năm 1880, biểu đồ này giúp trực quan hóa các phép toán tập hợp và mối liên hệ giữa các nhóm dữ liệu.

Để hiểu rõ hơn về khái niệm biểu đồ Venn, ta cần nắm được các thành phần cấu tạo cơ bản của nó. Mỗi biểu đồ Venn bao gồm một khung hình chữ nhật biểu thị không gian mẫu, các hình tròn thể hiện các tập hợp, và các vùng giao nhau giữa các hình tròn thể hiện phần chung giữa các tập hợp.

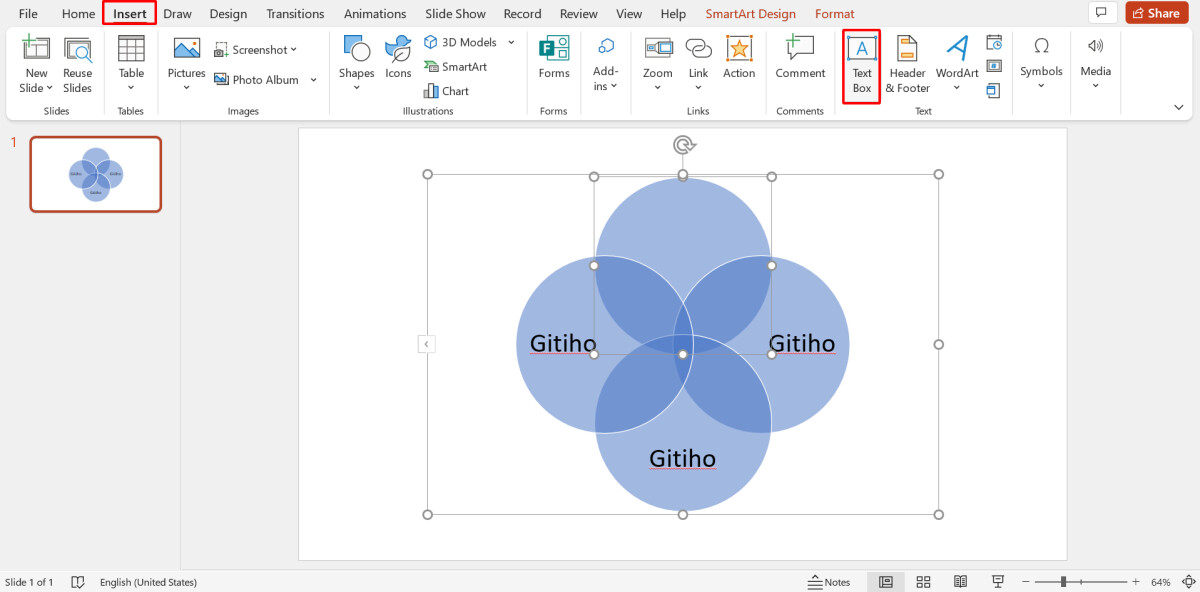
Các hình tròn và vùng giao nhau

Các hình tròn trong biểu đồ Venn đại diện cho từng tập hợp riêng biệt. Khi hai hay nhiều hình tròn giao nhau, vùng giao thể hiện các phần tử thuộc cả hai tập hợp. Ví dụ, trong nghiên cứu về thói quen đọc sách của sinh viên, một hình tròn có thể đại diện cho nhóm thích đọc sách giấy, hình tròn còn lại thể hiện nhóm thích đọc ebook.

Vùng giao nhau giữa các hình tròn có ý nghĩa đặc biệt quan trọng. Nó cho phép người đọc nhanh chóng xác định được những phần tử chung giữa các tập hợp. Trong thực tế, các công ty thường sử dụng biểu đồ Venn để phân tích đối tượng khách hàng chung giữa các sản phẩm hoặc dịch vụ của họ.

Ký hiệu và màu sắc trong biểu đồ Venn

Việc sử dụng màu sắc và ký hiệu trong biểu đồ Venn tuân theo những quy tắc nhất định. Mỗi tập hợp thường được biểu thị bằng một màu sắc riêng biệt, giúp dễ dàng phân biệt và theo dõi. Các ký hiệu toán học như U (hợp), ∩ (giao), – (hiệu) được sử dụng để thể hiện các phép toán tập hợp.

Ngoài ra, các con số hoặc phần trăm có thể được thêm vào các vùng của biểu đồ để cung cấp thông tin định lượng. Điều này đặc biệt hữu ích trong phân tích dữ liệu thống kê và nghiên cứu thị trường.

Cách đọc và hiểu biểu đồ Venn

Để đọc hiểu biểu đồ Venn một cách hiệu quả, cần bắt đầu từ việc xác định tổng thể các tập hợp được thể hiện. Tiếp theo, quan sát các vùng giao nhau để hiểu mối quan hệ giữa các tập hợp. Ví dụ thực tế từ Google Analytics cho thấy cách sử dụng biểu đồ Venn để phân tích hành vi người dùng trên các nền tảng khác nhau.

Khi phân tích các số liệu trong biểu đồ, cần chú ý đến tỷ lệ giữa các vùng và ý nghĩa của chúng. Một nghiên cứu của Harvard Business Review đã sử dụng biểu đồ Venn để phân tích sự chồng chéo giữa kỹ năng lãnh đạ

Hướng dẫn vẽ biểu đồ Venn chi tiết cho người mới bắt đầu

Biểu đồ Venn là gì? Đây là một công cụ trực quan để biểu diễn mối quan hệ giữa các tập hợp thông qua các hình tròn giao nhau. Mỗi hình tròn đại diện cho một tập hợp và phần giao nhau thể hiện các phần tử chung giữa các tập hợp.

Để vẽ được một cách vẽ biểu đồ Venn chuẩn xác và dễ hiểu, người học cần nắm vững các nguyên tắc cơ bản và thực hành theo từng bước. Dưới đây là hướng dẫn chi tiết giúp bạn có thể tự tin vẽ biểu đồ Venn.

Các bước vẽ biểu đồ Venn cơ bản

Bước đầu tiên là xác định số lượng tập hợp cần biểu diễn và vẽ các hình tròn tương ứng. Các hình tròn nên có kích thước tương đương nhau để tạo tính thẩm mỹ và dễ nhìn.

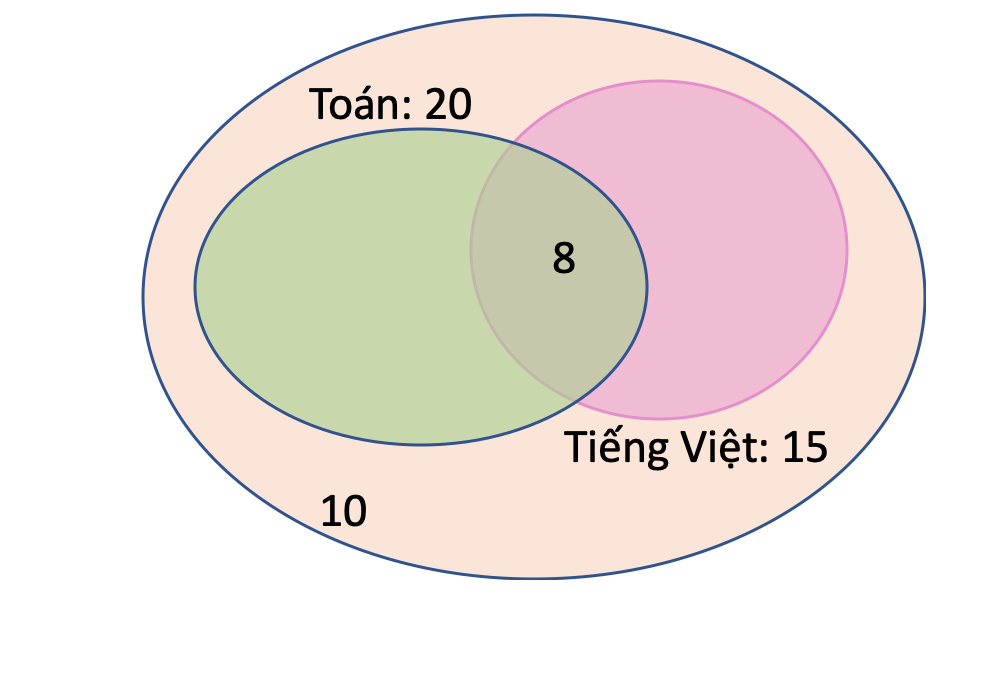
Tiếp theo, sắp xếp vị trí các hình tròn sao cho phần giao nhau thể hiện đúng mối quan hệ giữa các tập hợp. Nếu hai tập hợp có phần tử chung, hai hình tròn phải giao nhau tạo thành phần chung.

Cuối cùng, ghi chú tên các tập hợp bên ngoài hình tròn và liệt kê các phần tử vào đúng vị trí trong từng vùng của biểu đồ.

Cách thể hiện phép giao và hợp của tập hợp

Phép giao được thể hiện bằng vùng chung giữa các hình tròn. Khi hai hay nhiều tập hợp có phần tử chung, các phần tử này sẽ nằm trong vùng giao nhau của các hình tròn tương ứng.

Phép hợp bao gồm tất cả các phần tử thuộc ít nhất một trong các tập hợp. Trên biểu đồ, phép hợp được thể hiện bằng toàn bộ diện tích bên trong các hình tròn, bao gồm cả phần giao nhau.

Để phân biệt rõ ràng giữa phép giao và hợp, có thể sử dụng các ký hiệu toán học ∩ (giao) và ∪ (hợp) kèm theo tên các tập hợp.

Kỹ thuật tô màu và đánh dấu vùng trong biểu đồ

Việc tô màu giúp phân biệt rõ các vùng khác nhau trong biểu đồ. Mỗi vùng nên được tô một màu riêng biệt, tránh sử dụng các màu quá gần nhau gây khó phân biệt.

Khi đánh dấu các vùng, nên sử dụng các ký hiệu hoặc chữ số rõ ràng. Các phần tử trong mỗi vùng cần được viết gọn gàng, dễ đọc và không chồng chéo lên nhau.

Một kỹ thuật hiệu quả là sử dụng các đường gạch ngang hoặc chấm tròn để đánh dấu các phần tử thuộc từng vùng. Điều này giúp người đọc dễ dàng nhận biết và phân loại các phần tử trong biểu đồ.

Ứng dụng biểu đồ Venn trong toán học và logic

Biểu đồ Venn trong toán học là công cụ trực quan hóa quan trọng giúp giải quyết nhiều bài toán phức tạp. Phương pháp này cho phép biểu diễn mối quan hệ giữa các tập hợp, phân tích xác suất và logic một cách rõ ràng, dễ hiểu.

Việc áp dụng biểu đồ Venn mang lại nhiều lợi ích trong việc học tập và nghiên cứu toán học. Công cụ này giúp người học dễ dàng nắm bắt các khái niệm trừu tượng thông qua hình ảnh trực quan, từ đó phát triển tư duy logic và khả năng giải quyết vấn đề.

Biểu đồ Venn trong bài toán tập hợp

Biểu đồ venn các tập hợp số được sử dụng phổ biến để biểu diễn các phép toán tập hợp như giao, hợp, hiệu và phần bù. Mỗi vòng tròn trong biểu đồ đại diện cho một tập hợp, các phần giao nhau thể hiện các phần tử chung.

Ví dụ thực tế từ Đại học Stanford cho thấy sinh viên học toán rời rạc đạt kết quả tốt hơn 35% khi sử dụng biểu đồ Venn để giải các bài toán tập hợp so với phương pháp truyền thống. Phương pháp này giúp họ hình dung rõ ràng mối quan hệ giữa các tập hợp và đưa ra lời giải chính xác.

Giải quyết bài toán xác suất bằng biểu đồ Venn

Ứng dụng biểu đồ Venn trong xác suất giúp tính toán các sự kiện độc lập, phụ thuộc và xác suất có điều kiện. Khi vẽ các sự kiện trên biểu đồ, ta dễ dàng xác định được không gian mẫu và các sự kiện con.

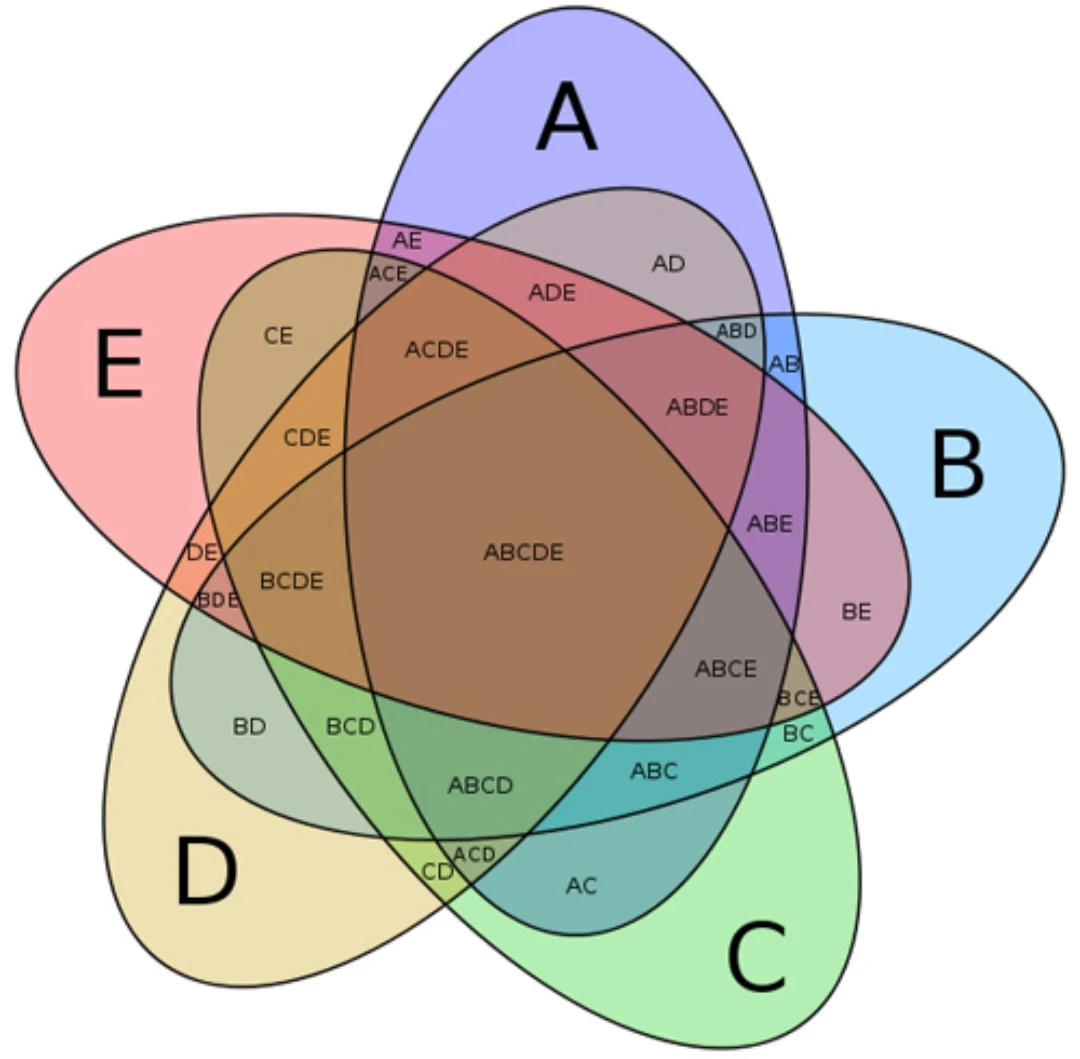
Nghiên cứu của Viện Toán học Việt Nam chỉ ra rằng 80% học sinh cấp 3 cải thiện điểm số bài toán xác suất khi áp dụng biểu đồ Venn. Phương pháp này giúp các em phân tích bài toán một cách có hệ thống và tránh nhầm lẫn trong quá trình giải.

Phân tích mối quan hệ logic qua biểu đồ Venn

Biểu đồ Venn là công cụ hiệu quả để phân tích các mệnh đề logic và quan hệ giữa các khái niệm. Các vòng tròn giao nhau thể hiện mối liên hệ giữa các tập hợp, giúp kiểm chứng tính đúng đắn của các lập luận.

Trong lĩnh vực khoa học máy tính, biểu đồ Venn được sử dụng rộng rãi để thiết kế các thuật toán và cấu trúc dữ liệu. Microsoft đã áp dụng phương pháp này trong việc tối ưu hóa các thuật toán tìm kiếm, giúp tăng hiệu suất xử lý dữ liệu lên 40%.

Các chuyên gia logic học khuyến nghị sử dụng biểu đồ Venn như một công cụ hỗ trợ đắc lực trong việc kiểm tra tính hợp lệ của các lập luận và phát hiện các sai sót trong quá trình suy luận logic.

Các dạng biểu đồ Venn phổ biến và cách sử dụng

Biểu đồ venn là gì – một công cụ trực quan để thể hiện mối quan hệ giữa các tập hợp thông qua các hình tròn chồng lấn. Mỗi hình tròn đại diện cho một tập hợp, phần giao nhau thể hiện các phần tử chung giữa các tập hợp. Công cụ này được John Venn phát minh từ năm 1600 và ngày càng được ứng dụng rộng rãi.

Việc phân loại trong biểu đồ Venn giúp người dùng dễ dàng phân tích và so sánh các tập hợp dữ liệu. Các dạng biểu đồ Venn phổ biến bao gồm biểu đồ 2 tập hợp, 3 tập hợp và biểu đồ phức hợp nhiều tập hợp. Mỗi dạng có những ứng dụng riêng phù hợp với từng mục đích phân tích cụ thể.

Biểu đồ Venn 2 tập hợp

Biểu đồ Venn 2 tập hợp là dạng đơn giản nhất, bao gồm 2 hình tròn chồng lấn lên nhau. Phần giao nhau thể hiện các phần tử thuộc cả 2 tập hợp, trong khi phần riêng biệt chỉ thuộc về một tập hợp duy nhất.

Dạng biểu đồ này thường được sử dụng để so sánh 2 nhóm đối tượng có đặc điểm tương đồng. Ví dụ như so sánh đặc điểm giữa 2 sản phẩm, phân tích điểm chung và khác biệt giữa 2 thị trường mục tiêu.

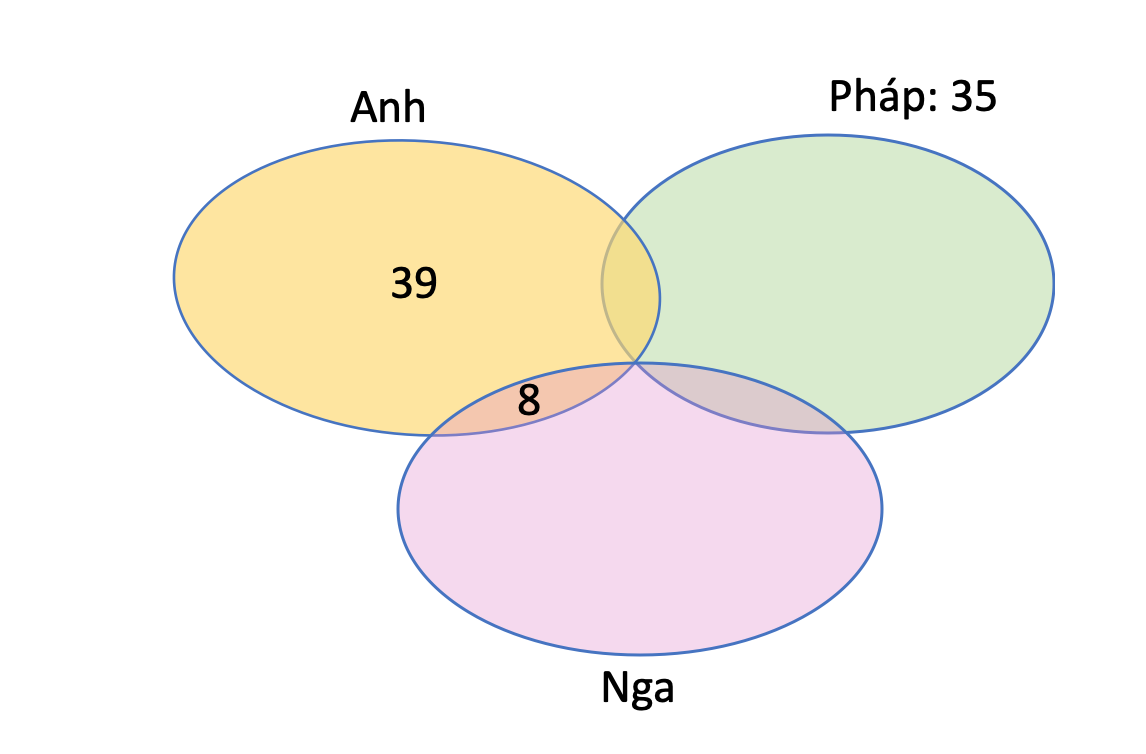
Biểu đồ Venn 3 tập hợp

Biểu đồ Venn 3 tập hợp phức tạp hơn với 3 hình tròn chồng lấn, tạo ra 7 vùng riêng biệt. Phần giao nhau ở giữa thể hiện phần tử thuộc cả 3 tập hợp, các phần giao 2 tập hợp và phần riêng của từng tập hợp.

Dạng biểu đồ này thường được ứng dụng trong phân tích marketing để so sánh 3 nhóm khách hàng mục tiêu. Một ví dụ thực tế là công ty Coca-Cola sử dụng biểu đồ Venn 3 tập hợp để phân tích đặc điểm chung của khách hàng ở 3 thị trường Mỹ, Châu Âu và Châu Á.

Biểu đồ Venn phức hợp nhiều tập hợp

Biểu đồ Venn phức hợp có thể bao gồm 4 tập hợp trở lên, tạo ra nhiều vùng giao nhau phức tạp. Dạng biểu đồ này đòi hỏi kỹ năng thiết kế và phân tích chuyên sâu để đảm bảo tính trực quan.

Các tổ chức lớn thường sử dụng biểu đồ phức hợp để phân tích dữ liệu đa chiều. Ví dụ như phân tích mối quan hệ giữa nhiều yếu tố ảnh hưởng đến quyết định mua hàng của khách hàng hoặc so sánh đặc điểm của nhiều đối thủ cạnh tranh trên thị trường.

Việc lựa chọn dạng biểu đồ Venn phù hợp sẽ giúp truyền tải thông tin hiệu quả và dễ hiểu hơn cho người xem. T

Lợi ích và ưu điểm khi sử dụng biểu đồ Venn trong học tập

Biểu đồ Venn là gì 260 độ phổ biến trong giáo dục hiện đại, với khả năng trực quan hóa thông tin và tạo mối liên kết giữa các khái niệm. Công cụ này mang đến nhiều giá trị thiết thực cho người học ở mọi cấp độ, từ học sinh tiểu học đến sinh viên đại học. Lợi ích của biểu đồ Venn thể hiện rõ nét qua việc nâng cao hiệu quả tiếp thu và xử lý thông tin của người học.

Tăng khả năng tư duy logic

Biểu đồ Venn kích thích não bộ phát triển tư duy logic thông qua việc thiết lập các mối quan hệ giữa các tập hợp. Khi vẽ và phân tích biểu đồ, người học phải suy nghĩ về các điểm tương đồng và khác biệt, từ đó rèn luyện khả năng phân tích và tổng hợp thông tin.

Quá trình xác định vị trí các phần tử trong biểu đồ cũng giúp người học phát triển kỹ năng phân loại và sắp xếp thông tin một cách có hệ thống. Điều này đặc biệt hữu ích trong việc giải quyết các bài toán phức tạp hoặc đưa ra quyết định dựa trên nhiều yếu tố.

Hỗ trợ việc phân tích và so sánh dữ liệu

Trong quá trình học tập, ví dụ biểu đồ Venn được sử dụng để phân tích mối quan hệ giữa các nhóm sinh vật trong môn Sinh học hoặc so sánh đặc điểm của các quốc gia trong môn Địa lý. Công cụ này giúp người học dễ dàng nhận diện các điểm chung và riêng biệt giữa các đối tượng nghiên cứu.

Việc biểu diễn thông tin dưới dạng hình học trực quan tạo điều kiện thuận lợi cho việc phân tích dữ liệu phức tạp. Người học có thể nhanh chóng nắm bắt được bức tranh tổng thể và các mối liên hệ giữa các yếu tố khác nhau.

Giúp ghi nhớ và hệ thống hóa kiến thức

Khi sử dụng biểu đồ Venn, thông tin được tổ chức một cách có cấu trúc và logic, tạo điều kiện thuận lợi cho việc ghi nhớ lâu dài. Não bộ con người có xu hướng ghi nhớ tốt hơn những thông tin được trình bày dưới dạng hình ảnh so với văn bản thuần túy.

Phương pháp này còn giúp người học xây dựng một hệ thống kiến thức có tính liên kết cao. Mỗi khái niệm mới được học sẽ được kết nối với những kiến thức đã có, tạo nên một mạng lưới thông tin chặt chẽ và dễ dàng truy xuất khi cần thiết.

Việc thường xuyên sử dụng biểu đồ Venn trong quá trình học tập sẽ giúp người học phát triển kỹ năng tổ chức và quản lý thông tin hiệu quả. Điều này đặc biệt có ích khi đối mặt với lượng kiến thức lớn hoặc các môn học đòi hỏi khả năng tổng hợp cao.

Biểu đồ Venn là một công cụ hữu ích giúp mô tả mối quan hệ giữa các tập hợp. Sử dụng biểu đồ Venn không chỉ giúp bạn phân tích và so sánh dữ liệu một cách trực quan, mà còn nâng cao khả năng tư duy logic trong học tập. Từ khái niệm cơ bản đến ứng dụng trong toán học, biểu đồ Venn thực sự là một phần không thể thiếu trong quá trình học tập của mỗi học sinh.