Chu trình Euler là một khái niệm quan trọng trong lý thuyết đồ thị, được đặt theo tên nhà toán học Leonhard Euler. Nó mô tả một đường đi đặc biệt trong đồ thị vô hướng, đi qua tất cả các cạnh đúng một lần và có điểm đầu trùng với điểm cuối. Trong bài viết dưới đây, cùng Hocthenao.vn tìm hiểu về khái niệm, định lý và ứng dụng của chu trình này trong thực tế nhé.
Khái niệm chu trình Euler
Đầu tiên, chúng ta cùng đi tìm hiểu về khái niệm và lịch sử hình thành chu trình này trước nhé.
Chu trình Euler là gì?
Chu trình Euler là chu trình đi qua tất cả các cạnh của đồ thị vô hướng đúng một lần. Trong đó:
- Đồ thị vô hướng: là đồ thị mà các cạnh không có hướng.
- Đường đi: là một dãy các cạnh liên kết các đỉnh của đồ thị, trong đó mỗi cạnh chỉ xuất hiện một lần.
- Chu trình: là đường đi mà điểm đầu trùng với điểm cuối.
Các khái niệm liên quan
Bên cạnh khái niệm chính, bạn cần nằm được những khái niệm liên quan như sau:
- Đường đi Euler là đường đi đơn của tất cả các cạnh thuộc một đồ thị.
- Đồ thị Euler là đồ thị có chứa chu trình Euler trong đó.
- Đồ thị nửa Euler là đồ thị chỉ chứa đường đi Euler.
Lịch sử hình thành
Vậy khái niệm đồ thị Euler là gì có từ khi nào? Khái niệm này xuất hiện từ bài toán bảy cây cầu Königsberg nổi tiếng, được nhà toán học Euler giải quyết vào khoảng năm 1736. Bài toán bảy cây cầu Königsberg như sau:
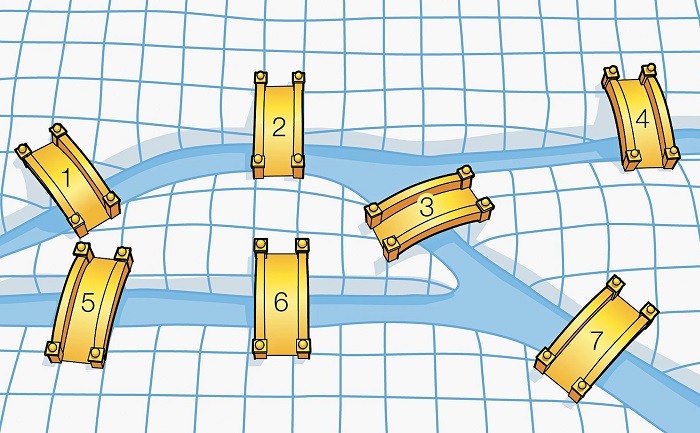
Vào thế kỷ 18, thành phố Königsberg (nay là Kaliningrad, Nga) có bảy hòn đảo được nối liền bởi bảy cây cầu. Người dân địa phương thắc mắc liệu có thể đi dạo qua tất cả các cây cầu mà không lặp lại bất kỳ cây cầu nào hay không.
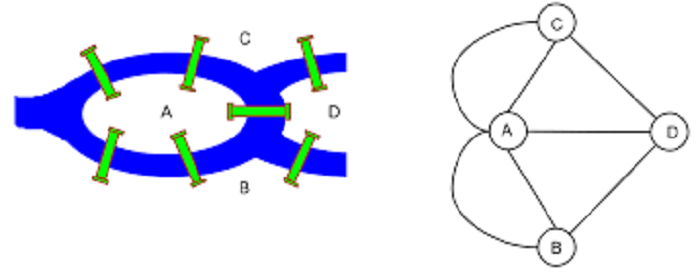
Euler đã mô hình hóa bài toán này bằng một đồ thị vô hướng, trong đó mỗi đỉnh ứng với một hòn đảo và mỗi cạnh ứng với một cây cầu. Sau khi phân tích đồ thị, Euler nhận ra rằng không có cách nào để hoàn thành chuyến đi dạo mà không lặp lại bất kỳ cây cầu nào.
Lý do là vì:
- Mỗi hòn đảo đều có bậc lẻ (số lượng cạnh nối với hòn đảo đó là số lẻ).
- Theo định lý bắt tay, trong một đồ thị vô hướng, tổng bậc của tất cả các đỉnh là số chẵn.
- Do đó, không thể có chu trình đi qua tất cả các cạnh đúng một lần trong đồ thị này.
Từ đó suy ra phương trình Euler có công thức như sau:
V – E + F = 2
Trong đó:
- V: Số lượng đỉnh (điểm) của đa diện.
- E: Số lượng cạnh của đa diện.
- F: Số lượng mặt (đa giác) của đa diện.
Định lý Euler và hệ quả
Một đồ thị vô hướng liên thông G = (V, E) có chu trình Euler khi và chỉ khi:
- Mọi đỉnh đều có bậc chẵn: deg(v) = 0 (mod 2)∀ v∈ V.
- Đồ thị có ít nhất hai đỉnh có bậc lẻ.
Từ định lý Euler, ta có các hệ quả sau:
- Một đồ thị vô hướng có ít nhất hai đỉnh bậc lẻ không thể có chu trình Euler.
- Một đồ thị vô hướng liên thông có chu trình Euler khi và chỉ khi nó có không quá hai đỉnh bậc lẻ.
- Đồ thị vô hướng Euler là đồ thị vô hướng liên thông mà mọi đỉnh đều có bậc chẵn.
Chứng minh định lý Euler
Ta có thể chứng minh định lý Euler theo 2 cách: hướng đi và hướng ngược lại:
Hướng đi: Chứng minh bằng quy nạp theo số lượng cạnh:
Trường hợp cơ bản: Đồ thị có 0 cạnh, không có chu trình Euler.
Bước quy nạp: Giả sử định lý đúng với đồ thị có n cạnh, n > 0. Xét đồ thị G có n + 1 cạnh. Chọn một cạnh bất kỳ e. Nếu cả hai đỉnh u và v của e đều có bậc chẵn, thì có thể loại bỏ e và G sẽ trở thành đồ thị có n cạnh thỏa mãn định lý. Nếu u hoặc v có bậc lẻ, G sẽ có ít nhất 2 đỉnh bậc lẻ. Ta có thể chọn một chu trình Euler trong G không đi qua e, sau đó thêm e vào chu trình để tạo thành chu trình Euler trong G có n + 1 cạnh.
Hướng ngược lại
Giả sử G có chu trình Euler C. Ta đi qua C theo thứ tự, mỗi khi đi qua một đỉnh v, ta tăng bậc của v lên 2. Vì C đi qua tất cả các cạnh, nên bậc của mọi đỉnh đều tăng lên 2. Do đó, mọi đỉnh đều có bậc chẵn.
Xét một đỉnh v bất kỳ trong G. Ta có thể đi từ v theo một đường đi Euler P đến một đỉnh u khác. Do C là chu trình Euler, ta có thể đi tiếp từ u theo C để quay lại v. Do đó, bậc của v là chẵn.
Xét một đỉnh w có bậc lẻ. Ta có thể đi từ w theo một đường đi Euler P đến một đỉnh v. Do bậc của w là lẻ, nên bậc của v phải là lẻ. Do đó, G có ít nhất hai đỉnh bậc lẻ.
Ứng dụng của đồ thị Euler
Đồ thị Euler có nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Tìm đường đi
Thuật toán Fleury có thể được sử dụng để tìm đường đi Euler trong một đồ thị vô hướng. Sau đó, có thể sử dụng đường đi Euler này để tìm đường đi ngắn nhất giữa hai điểm bất kỳ trong đồ thị. Ngoài ra, chu trình Euler được sử dụng để tìm đường đi qua tất cả các điểm trong một đồ thị vô hướng. Euler C++ rất hữu ích cho các ứng dụng như lập bản đồ, định vị, và robot.
Kiểm tra tính kết nối
Một đồ thị vô hướng có liên thông khi và chỉ khi nó có chu trình Euler. Do đó, có thể sử dụng thuật toán tìm chu trình Euler để kiểm tra xem một đồ thị có liên thông hay không.
Một đồ thị Euler có thể được chia thành các thành phần liên thông, là các tập con của các đỉnh mà mỗi đỉnh trong tập con đều có thể đi đến bất kỳ đỉnh nào khác trong cùng tập con bằng một đường đi. Thuật toán Hierholzer có thể được sử dụng để tìm các thành phần liên thông trong một đồ thị vô hướng.
Giải các bài toán về đồ thị
Bài toán người bán rong là bài toán về việc tìm đường đi ngắn nhất cho một người bán rong để đi qua tất cả các ngôi nhà trong một khu phố và quay trở lại điểm xuất phát. Bài toán này có thể được giải quyết bằng cách sử dụng thuật toán Fleury để tìm chu trình Euler trong đồ thị mô tả các ngôi nhà và các con đường.
Các lĩnh vực khác
Thuật toán Euler có thể được sử dụng để mã hóa và giải mã thông tin. Ví dụ, có thể sử dụng chu trình Euler để tạo ra một hệ thống mã hóa trong đó mỗi ký tự được biểu diễn bằng một chuỗi các cạnh trong đồ thị. Ngoài ra, nó có thể được sử dụng để thiết kế mạng lưới giao thông, hệ thống điện lực,… để đảm bảo rằng tất cả các phần của mạng lưới đều được kết nối với nhau.
Lời kết
Chu trình Euler là một khái niệm quan trọng trong lý thuyết đồ thị với nhiều ứng dụng thực tế. Hiểu biết về chu trình này có thể giúp giải quyết các bài toán về thiết kế mạng lưới, tìm đường đi, và kiểm tra tính kết nối của đồ thị.