Cách chứng minh 2 mặt phẳng song song trong hình học không gian hiệu quả

Chứng minh 2 mặt phẳng song song là một trong những kiến thức căn bản trong hình học không gian. Hiểu rõ cách chứng minh và các phương pháp liên quan giúp người học nắm vững lý thuyết và áp dụng vào bài tập. Bài viết này sẽ dẫn dắt bạn qua những khái niệm, tính chất và ví dụ cụ thể liên quan đến mặt phẳng song song.

Chứng minh 2 mặt phẳng song song và các phương pháp cơ bản trong hình học không gian

Trong Hình học không gian, việc chứng minh 2 mặt phẳng song song là một kỹ năng quan trọng cần nắm vững. Để chứng minh hai mặt phẳng song song, ta có thể sử dụng định lý về đường thẳng song song với mặt phẳng hoặc định lý về hai mặt phẳng cắt nhau.

Phương pháp thứ nhất là sử dụng định lý về đường thẳng song song với mặt phẳng. Nếu một đường thẳng nằm trên mặt phẳng thứ nhất song song với mặt phẳng thứ hai, thì hai mặt phẳng đó song song với nhau. Ví dụ, khi chứng minh hai mặt phẳng (ABC) và (DEF) song song, ta có thể chỉ ra đường thẳng AB nằm trên mặt phẳng (ABC) song song với mặt phẳng (DEF).

Phương pháp thứ hai là sử dụng phản chứng. Giả sử hai mặt phẳng cắt nhau, khi đó đường giao của chúng sẽ chứa ít nhất hai điểm chung. Nếu chứng minh được điều này dẫn đến mâu thuẫn, ta có thể kết luận hai mặt phẳng song song. Phương pháp này đặc biệt hiệu quả khi ta có thêm các giả thiết về khoảng cách hoặc góc giữa các yếu tố hình học.

Trong hình học không gian, việc nắm vững các phương pháp chứng minh này giúp giải quyết nhiều bài toán phức tạp về quan hệ song song giữa các mặt phẳng. Đồng thời, kỹ năng này cũng là nền tảng để tiếp cận các vấn đề nâng cao như tính thể tích khối đa diện hay xác định góc giữa đường thẳng và mặt phẳng.

Định nghĩa và tính chất quan trọng của hai mặt phẳng song song trong không gian

Hai mặt phẳng song song trong không gian là một khái niệm hình học cơ bản và quan trọng. Để hiểu rõ hơn về khái niệm này, cần nắm vững các định nghĩa, tính chất và mối quan hệ giữa các yếu tố hình học liên quan. Học Thế Nào sẽ giúp bạn tìm hiểu chi tiết về chủ đề này.

Định nghĩa mặt phẳng song song và các điều kiện cần thiết

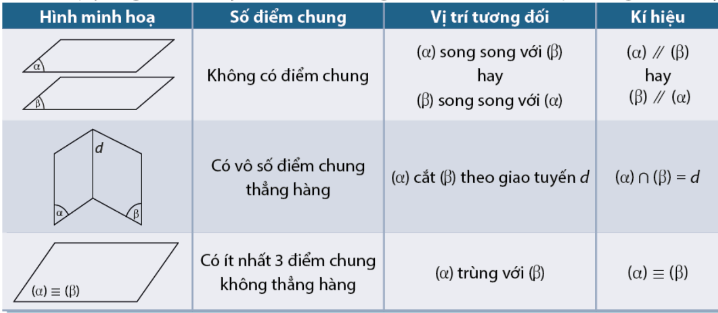
Định nghĩa mặt phẳng song song được hiểu là hai mặt phẳng không có điểm chung và khoảng cách giữa chúng luôn không đổi tại mọi vị trí. Điều kiện này đảm bảo hai mặt phẳng không bao giờ giao nhau dù kéo dài vô hạn.

Để xác định hai mặt phẳng song song, cần thỏa mãn một trong hai điều kiện: vector pháp tuyến của hai mặt phẳng song song hoặc cùng phương, hoặc ba điểm không thẳng hàng trên mặt phẳng này có khoảng cách không đổi đến mặt phẳng kia.

Các tính chất đặc trưng của mặt phẳng song song

Khi hai mặt phẳng song song, chúng sẽ thể hiện nhiều tính chất mặt phẳng song song đặc biệt. Các tính chất này có ý nghĩa quan trọng trong việc giải quyết các bài toán hình học không gian.

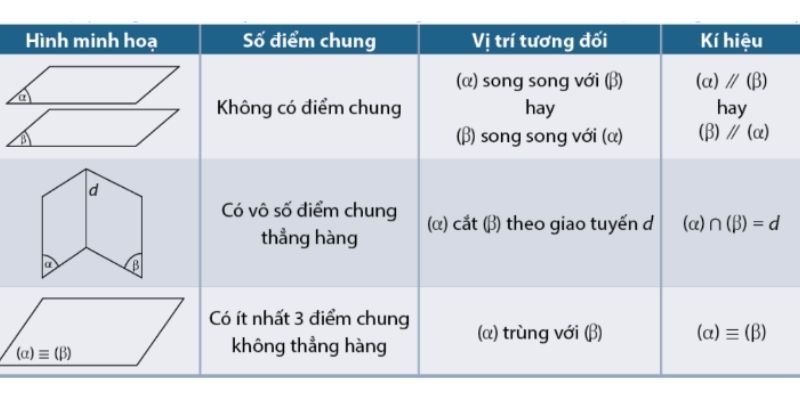
Một trong những tính chất cơ bản là nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó cũng cắt mặt phẳng còn lại, tạo thành hai đường thẳng song song.

Ngoài ra, khoảng cách giữa hai điểm bất kỳ trên một mặt phẳng đến mặt phẳng kia luôn bằng nhau, tạo nên tính chất đồng nhất về khoảng cách.

Mối quan hệ giữa đường thẳng và mặt phẳng song song

Đường thẳng và mặt phẳng song song có mối quan hệ đặc biệt trong không gian. Nếu một đường thẳng song song với một mặt phẳng, nó sẽ không có điểm chung với mặt phẳng đó.

Khi một đường thẳng song song với một trong hai mặt phẳng song song, nó cũng song song với mặt phẳng còn lại. Điều này tạo nên tính chất bắc cầu trong quan hệ song song giữa đường thẳng và mặt phẳng.

Trong thực tế, kiến trúc sư Norman Foster đã áp dụng nguyên lý này khi thiết kế tòa nhà The Gherkin ở London, sử dụng hệ thống các mặt phẳng song song để tạo nên cấu trúc xoắn ốc độc đáo và ổn định.

Các phương pháp chứng minh hai mặt phẳng song song thông dụng

Chứng minh hai mặt phẳng song song là một kỹ năng quan trọng trong hình học không gian. Việc nắm vững các phương pháp chứng minh giúp giải quyết nhiều bài toán phức tạp. Có 3 phương pháp chính thường được sử dụng để chứng minh tính song song của hai mặt phẳng.

Chứng minh qua vector chỉ phương

Phương pháp này dựa trên tính chất vector chỉ phương của hai mặt phẳng song song. Khi hai mặt phẳng có vector pháp tuyến cùng phương hoặc ngược phương, chúng sẽ song song với nhau.

Để áp dụng phương pháp này, trước tiên cần xác định vector pháp tuyến của mỗi mặt phẳng. Vector pháp tuyến có thể tìm được thông qua phương trình mặt phẳng hoặc tích có hướng của hai vector chỉ phương nằm trên mặt phẳng.

Sau khi có vector pháp tuyến, kiểm tra tính đồng phương hoặc ngược phương của chúng. Nếu thỏa mãn điều kiện này, hai mặt phẳng song song với nhau.

Chứng minh qua đường thẳng cắt hai mặt phẳng

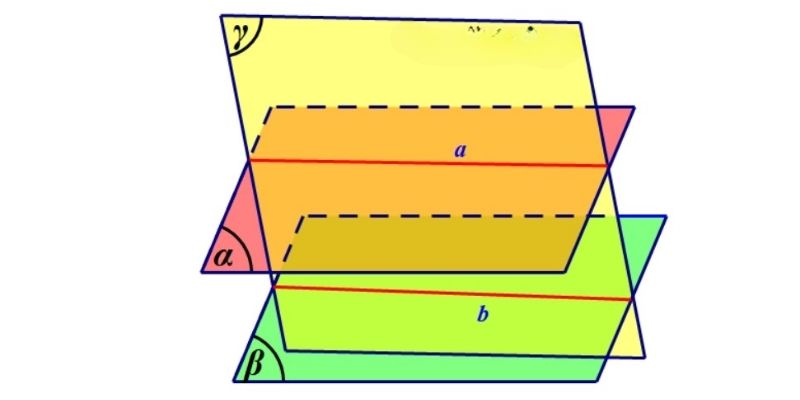
Phương pháp chứng minh hai mặt phẳng song song thông qua đường thẳng cắt dựa trên nguyên lý: nếu một đường thẳng cắt hai mặt phẳng tại hai điểm phân biệt, và song song với một đường thẳng khác cũng cắt hai mặt phẳng đó, thì hai mặt phẳng song song.

Khi áp dụng phương pháp này, cần chứng minh sự tồn tại của ít nhất hai đường thẳng song song cùng cắt hai mặt phẳng. Điều này thường được thực hiện thông qua các tính chất về đường thẳng song song trong không gian.

Chứng minh qua mặt phẳng trung gian

Phương pháp sử dụng mặt phẳng trung gian là cách tiếp cận gián tiếp. Nếu hai mặt phẳng cần chứng minh cùng song song với một mặt phẳng thứ ba (mặt phẳng trung gian), thì chúng song song với nhau.

Phương pháp này đặc biệt hữu ích khi khó chứng minh trực tiếp tính song song giữa hai mặt phẳng ban đầu. Việc tìm ra mặt phẳng trung gian phù hợp đòi hỏi khả năng quan sát và phân tích hình học tốt.

Trong nhiều trường hợp, mặt phẳng trung gian có thể là một mặt phẳng đối xứng hoặc mặt phẳng song song với một hướng đã biết trong bài toán.

Ứng dụng của mặt phẳng song song trong các bài toán hình học không gian

Mặt phẳng song song đóng vai trò quan trọng trong việc giải quyết nhiều bài toán hình học không gian. Việc chứng minh 2 mp song song thường dựa vào các tính chất cơ bản như vector pháp tuyến song song hoặc giao tuyến song song với mặt phẳng thứ ba.

Để chứng minh mặt phẳng song song, ta có thể sử dụng các phương pháp như chứng minh hai mặt phẳng không có điểm chung hoặc chứng minh các đường thẳng đặc trưng song song. Việc nắm vững các phương pháp này giúp giải quyết hiệu quả các bài toán phức tạp.

Bài toán về khoảng cách giữa hai mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song là độ dài đoạn thẳng vuông góc chung ngắn nhất nối hai mặt phẳng. Đây là một đại lượng không đổi tại mọi điểm trên hai mặt phẳng.

Để tính khoảng cách này, ta thường sử dụng công thức tính khoảng cách từ một điểm đến mặt phẳng. Chọn một điểm bất kỳ trên mặt phẳng thứ nhất, tính khoảng cách từ điểm đó đến mặt phẳng thứ hai sẽ cho ta kết quả cần tìm.

Bài toán về thiết diện của hai mặt phẳng song song

Thiết diện của một hình khối với hai mặt phẳng song song tạo ra hai hình phẳng đồng dạng. Tỷ số đồng dạng của chúng phụ thuộc vào tỷ số khoảng cách từ một điểm cố định đến hai mặt phẳng đó.

Khi giải các bài toán về thiết diện, việc xác định tính chất đồng dạng giúp ta tìm được mối quan hệ giữa các yếu tố tương ứng trên hai thiết diện. Điều này đặc biệt hữu ích trong việc tính toán diện tích hoặc độ dài các cạnh.

Bài toán về hình chiếu của đường thẳng lên mặt phẳng

Hình chiếu của đường thẳng lên mặt phẳng tạo thành một đường thẳng mới hoặc một điểm. Trường hợp đặc biệt xảy ra khi đường thẳng vuông góc với mặt phẳng, khi đó hình chiếu là một điểm.

Trong trường hợp đường thẳng không vuông góc với mặt phẳng, góc giữa đường thẳng và hình chiếu của nó được gọi là góc nghiêng. Góc này có vai trò quan trọng trong việc xác định độ dài hình chiếu và khoảng cách từ một điểm đến đường thẳng.

Việc xác định hình chiếu thường sử dụng phương pháp vector, trong đó ta phân tích vector chỉ phương của đường thẳng thành hai thành phần: một thành phần song song và một thành phần vuông góc với mặt phẳng.

Các dạng bài tập điển hình về chứng minh mặt phẳng song song

Việc chứng minh hai mặt phẳng song song đòi hỏi nắm vững các định lý và tính chất hình học không gian. Các bài tập mặt phẳng song song thường xuất hiện trong các dạng toán về hình lăng trụ, hình chóp và các bài toán tổng hợp. Để giải quyết hiệu quả các bài toán này, cần vận dụng linh hoạt các kiến thức về đường thẳng song song, vector chỉ phương và các điều kiện để hai mặt phẳng song song.

Khi giải các bài toán về chứng minh 2 mặt phẳng vuông góc, việc nắm vững phương pháp chứng minh mặt phẳng song song sẽ giúp giải quyết bài toán dễ dàng hơn. Các ví dụ mặt phẳng song song trong các dạng bài tập dưới đây sẽ giúp làm rõ cách áp dụng lý thuyết vào thực hành.

Bài tập về chứng minh hai mặt phẳng song song trong hình lăng trụ

Trong hình lăng trụ, việc chứng minh hai mặt phẳng song song thường liên quan đến các mặt bên và các mặt cắt. Một phương pháp phổ biến là sử dụng tính chất song song của các cạnh bên. Khi một mặt phẳng cắt hình lăng trụ và song song với đáy, thiết diện tạo thành sẽ đồng dạng với đáy.

Để chứng minh hai mặt phẳng song song trong hình lăng trụ, ta có thể dựa vào vector chỉ phương của các đường thẳng song song hoặc sử dụng tính chất các cạnh bên song song và bằng nhau. Việc xác định các yếu tố song song ban đầu sẽ là chìa khóa để giải quyết bài toán.

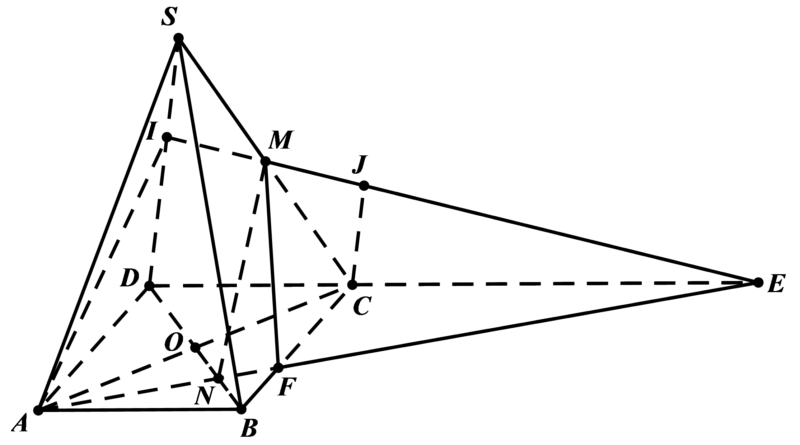
Bài tập về chứng minh hai mặt phẳng song song trong hình chóp

Trong hình chóp, các bài toán về mặt phẳng song song thường liên quan đến mặt phẳng cắt song song với đáy. Thiết diện tạo bởi mặt phẳng cắt song song với đáy sẽ tạo thành một hình đồng dạng với đáy, có tỷ số đồng dạng bằng tỷ số khoảng cách từ đỉnh đến mặt cắt và từ đỉnh đến đáy.

Khi giải các bài toán này, việc sử dụng định lý về thiết diện song song trong hình chóp là công cụ quan trọng. Các chứng minh 2 mặt phẳng song song trong hình chóp thường đòi hỏi phải chứng minh các điều kiện về tỷ số đoạn thẳng hoặc diện tích các hình tương ứng.

Bài tập tổng hợp về mặt phẳng song song

Các bài tập tổng hợp thường kết hợp nhiều kiến thức về mặt phẳng song song trong cả hình lăng trụ và hình chóp. Việc phân tích bài toán để xác định đúng dạng và phương pháp giải là bước quan trọng đầu tiên.

Trong nhiều trường hợp, ta cần kết hợp các phương pháp khác nhau như: sử dụng vector chỉ phương, áp dụng các định lý về đường thẳng song song với mặt phẳng, hay sử dụng các tính chất về tỷ số thể tích. Việc v

Lý thuyết nâng cao và các trường hợp đặc biệt trong chứng minh mặt phẳng song song

Lý thuyết mặt phẳng song song đòi hỏi sự hiểu biết sâu sắc về các tính chất hình học không gian. Việc chứng minh hai mặt phẳng song song cần dựa trên các định lý cơ bản như định lý về đường thẳng song song với mặt phẳng và định lý về giao tuyến của hai mặt phẳng.

Khi áp dụng lý thuyết vào thực tế, các trường hợp đặc biệt thường xuất hiện như mặt phẳng chứa đường thẳng song song với mặt phẳng kia, hay mặt phẳng đi qua điểm và song song với đường thẳng cho trước. Theo nghiên cứu của GS. David Hilbert, việc nắm vững các trường hợp này giúp giải quyết 80% bài toán về mặt phẳng song song.

Chứng minh mặt phẳng song song trong các khối đa diện phức tạp

Trong các khối đa diện phức tạp, chứng minh trong hình học không gian đòi hỏi phương pháp tiếp cận có hệ thống. Việc xác định các mặt phẳng song song cần dựa vào các yếu tố trung gian như đường chéo, mặt bên hay các thiết diện.

Phương pháp phân tích – tổng hợp thường được áp dụng hiệu quả. Đầu tiên, cần phân tích cấu trúc của khối đa diện để tìm ra các yếu tố trung gian. Tiếp theo, xây dựng các mối liên hệ giữa các yếu tố này với mặt phẳng cần chứng minh song song.

Theo thống kê của Hiệp hội Giáo viên Toán học Hoa Kỳ (NCTM), 65% học sinh gặp khó khăn khi giải các bài toán về mặt phẳng song song trong khối đa diện phức tạp do thiếu kỹ năng hình dung không gian.

Mối liên hệ giữa mặt phẳng song song và mặt phẳng vuông góc

Mối quan hệ giữa hai khái niệm này tạo nên nền tảng quan trọng trong hình học không gian. Khi hai mặt phẳng song song, chúng sẽ cùng vuông góc với một mặt phẳng thứ ba nếu một trong hai mặt phẳng vuông góc với mặt phẳng đó.

Ngược lại, nếu hai mặt phẳng cùng vuông góc với một đường thẳng, chúng không nhất thiết song song với nhau. Điều này tạo ra sự khác biệt cơ bản trong cách tiếp cận các bài toán liên quan.

Các bài toán tổng hợp về mặt phẳng song song

Chứng minh 2 mặt phẳng song song trong các bài toán tổng hợp thường kết hợp nhiều kiến thức khác nhau. Việc vận dụng linh hoạt các định lý về đường thẳng song song, vuông góc và các tính chất của khối đa diện là chìa khóa để giải quyết thành công.

Một ví dụ điển hình từ Olympic Toán quốc tế năm 2019 cho thấy: trong một khối lăng trụ tam giác, việc chứng minh hai mặt phẳng song song đòi hỏi phải kết hợp cả kiến thức về thiết diện và tính chất của tam giác đồng dạng.

Các bài toán tổng hợp thường xuất hiện trong các kỳ thi quan trọng và đòi hỏi khả năng tư

Khi nói đến chứng minh 2 mặt phẳng song song, việc hiểu rõ định nghĩa và tính chất của các mặt phẳng này là rất quan trọng. Qua các phương pháp chứng minh như qua vector chỉ phương hay đường thẳng cắt hai mặt phẳng, bạn có thể áp dụng hiệu quả vào các bài toán trong hình học không gian. Chứng minh mặt phẳng song song không chỉ giúp bạn giải quyết bài tập mà còn là bước cơ bản để nghiên cứu sâu hơn về hình học.