Hình tam giác cân là gì? Định nghĩa, tính chất và ứng dụng thực tế

Tam giác cân là một dạng hình tam giác có tính chất đặc biệt. Do đó nó có đầy đủ các tính chất của một hình tam giác thường và một số những đặc điểm đặc biệt khác. Để tìm hiểu chi tiết về hình tam giác cân là gì, bạn đọc hãy theo dõi ngay bài viết dưới đây.

Hình tam giác cân là gì?

Tam giác cân là một hình tam giác và có 2 cạnh bằng nhau. Đây là một dạng hình học được nhắc đến rất nhiều trong các bài giảng. 

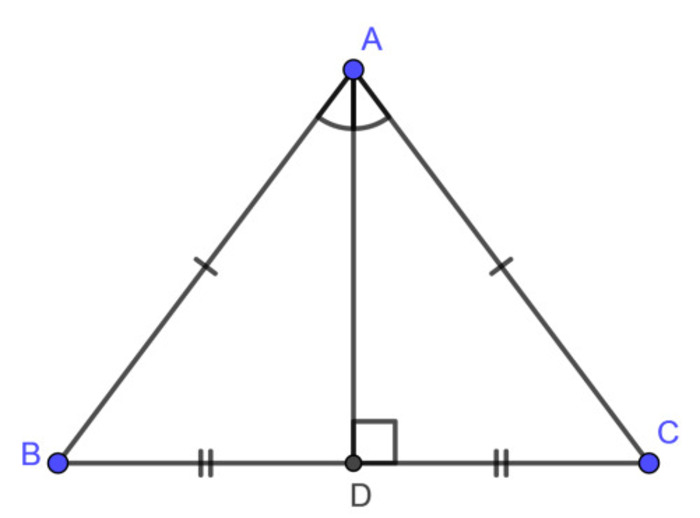
Tích chất tam giác cân

Từ định nghĩa tgc là gì, ta có được tính chất của hình như sau:

• Hai góc của tam giác cân tạo bởi 2 cạnh bên và cạnh đáy sẽ bằng nhau.
• Tam giác có hai cạnh bằng nhau thì chắc chắn đó là tam giác cân.
• Tam giác có hai góc bằng nhau cũng chắc chắn là tam giác cân.
• Đường trung tuyến từ đỉnh đến cạnh đáy vừa là đường cao và phân giác của góc đó.

Dấu hiệu nhận biết hình tam giác cân chính xác nhất

Dựa vào cạnh

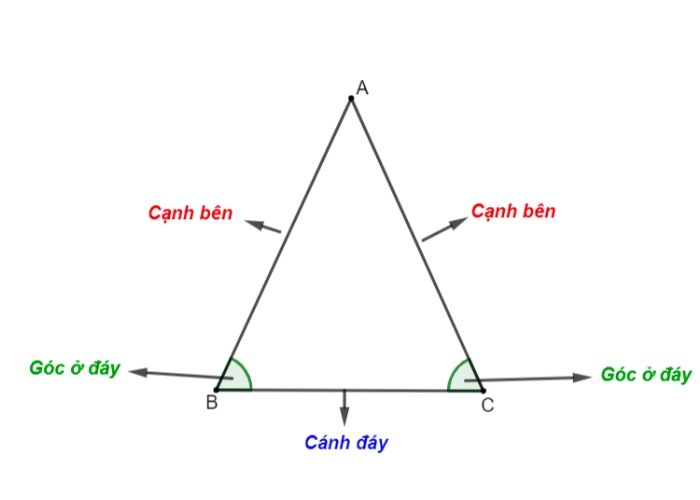
Nếu hình tam giác có hai cạnh đều bằng nhau thì đó là tam giác cân. Hai cạnh bằng nhau được gọi là cạnh bên, cạnh còn lại là cạnh đáy.

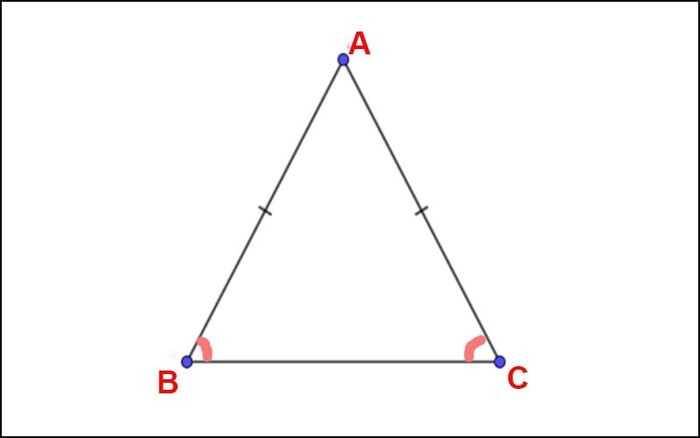
Ví dụ: Tam giác ABC có AB = AC nên ABC là tam giác cân.

Dựa vào góc

Nếu htg có hai góc bằng nhau thì đó là tam giác cân. Hai góc bằng nhau được gọi là góc ở đáy, đỉnh của tam giác cân là giao điểm của hai cạnh bên.

Ví dụ: Tam giác DEF có góc D = góc E nên DEF là tam giác cân.

Dựa vào đường trung tuyến, đường cao, đường trung trực

Đường trung tuyến nối từ đỉnh đối diện với cạnh đáy không chỉ là đường trung tuyến mà còn là đường cao, đường trung trực, và đường phân giác của góc tại đỉnh đó.

Ví dụ: Giả sử chúng ta có tam giác ABC, với cạnh đáy là BC và đỉnh đối diện là A. Đường trung tuyến từ A đến trung điểm D của BC (AD) không chỉ chia BC thành hai phần bằng nhau mà còn vuông góc với BC, chia góc A thành hai góc đều nhau và chia đôi cạnh BC.

Nói cách khác, trong tam giác ABC, nếu AD là: đường trung tuyến, đường cao, đường trung trực của BC, đường phân giác của góc BAC, thì tam giác đó có các tính chất đặc biệt của một tam giác cân.

Công thức tính chu vi và diện tích tgc

Chu vi tgc

Chu vi hình tam giác cân bằng công thức:

P = 2 x a + b

Trong đó P là chu vi của hình; a là độ dài của hai cạnh bên; b là độ dài của cạnh đáy.

Diện tích tgc

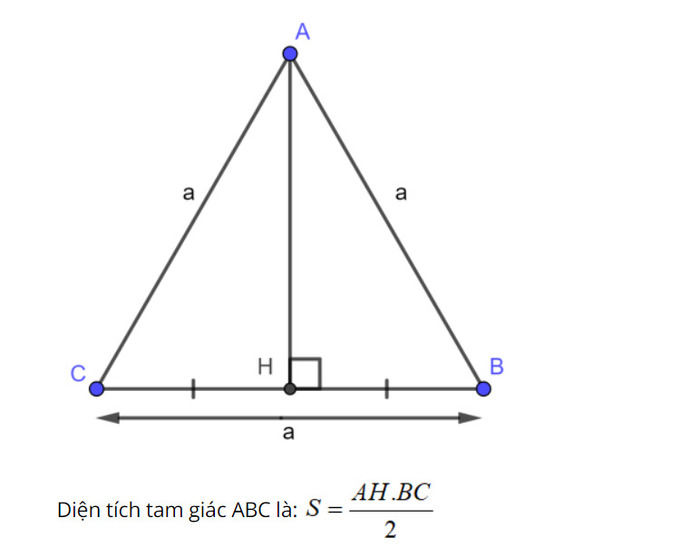
Ta có công thức tính diện tích hình tam giác cân như sau:

$$S\;=\;\frac12\;\times\;b\;\times\;h$$

Trong đó b là độ dài của cạnh đáy, h là chiều cao ứng với cạnh đáy.

Trong trường hợp đề bài chỉ cho số đo của 3 cạnh, ta hoàn toàn có thể tính được chiều cao khi áp dụng công thức Pythagoras. Chiều cao sẽ là cạnh của 1 góc vuông và được tính như sau:

$$h=\surd\lbrack a^2-(\frac b2)^2\rbrack$$

Ví dụ cách vẽ hình tam giác cân

Các bước đơn giản nhất để vẽ tam giác cân như sau:

• Ví dụ tam giác cần vẽ là ABC, đầu tiên sẽ xác định đỉnh là A và hai cạnh AB, AC bằng nhau.
• Xác định vị trí của điểm A, sau đó dùng thước đo đạc để xác định điểm B và C rồi nối các điểm lại với nhau.
• Dùng thước đo góc kiểm tra lại xem góc ABC và góc ABC đã bằng nhau hay chưa.

Một số dạng bài tập về tgc

Bài tập về tgc có rất đa dạng, trong đó sẽ phổ biến với một số ví dụ như ở dưới đây:

Ví dụ 1: Cho một hình tam giác cân ABC cân tại A. Nếu góc BAC bằng 70 độ thì số đo của hai góc còn lại sẽ là bao nhiêu?

Gợi ý giải: Vì tam giác cân sẽ có hai góc tạo bởi cạnh bên và đáy bằng nhau nên 2 góc cần tìm sẽ bằng nhau. Tổng 3 góc bằng 180 độ, từ đó suy ra tổng 2 góc còn lại là 110 độ, mỗi góc là 55 độ.

Ví dụ 2: Cho hình tam giác cân ABC với AB = AC. Trên đoạn BC có điểm D với BD = CD. Hãy chứng minh tam giác ABD vuông.

Gợi ý giải: Vẽ hình theo giả thuyết của đề bài. Ta có BD = CD, do đó D là trung điểm của BC. Mà tam giác ABC cân tại A nên AD vừa là trung tuyến, vừa là đường cao. Từ đó AD vuông góc với BC nên suy ra tam giác ABD vuông tại D.

Ví dụ 3: Giả sử tam giác XYZ vuông cân tại X. Tìm ra số đo các góc còn lại trong tam giác.

Gợi ý giải: Hình tam giác XYZ vuông cân tại X nên góc YXZ bằng 90 độ. Áp dụng công thức có thể tính được hai góc còn lại bằng nhau, tổng bằng 90 độ nên mỗi góc bằng 45 độ.

Xem thêm: Dạng bài toán chứng minh hình tam giác cân

Ứng dụng của tam giác cân trong thực tế

Tam giác cân có rất nhiều ứng dụng hữu ích và không thể thay thế trong thực tiễn. Cụ thể như sau:

• Trong xây dựng: Rất nhiều dạng thiết kế, kiến trúc sử dụng tam giác cân làm mẫu. Có thể kể đến những thứ gần gũi nhất như mái nhà,… Dạng hình tam giác cân sẽ có  năng chịu và phân tán lực rất tốt nên đây là lý do được ứng dụng nhiều.
• Trong khoa học, công nghiệp: Những loại máy móc thường thấy trong sản xuất cũng được tạo lập nhờ kết cấu của hình tam giác cân. Từ đó nâng cao hiệu suất hoạt động và đảm bảo sự chính xác, cân bằng.
• Trong hội hoạ, đo đạc: Bố cục là yếu tố quan trọng nhất quyết định tác phẩm có thuận mắt, hài hoà hay không. Một số hình học các dạng các cạnh đều nhau như tam giác, vuông, thoi,… đều có thể áp dụng trong ngành này.

Có thể khẳng định tam giác cân rất quan trọng trong đời sống của mỗi chúng ta. Từ những đồ vật gần gũi nhất cũng được ứng dụng dạng hình và các tính chất để giúp cuộc sống được tiện nghi hơn. Hiểu rõ kiến thức cơ bản hình tam giác cân là gì sẽ giúp ích được cho bạn đọc trong học tập và trên thực tiễn.