Tính diện tích hình quạt tròn qua công thức, bài tập và ứng dụng thực tế

Diện tích hình quạt tròn là một khái niệm quan trọng trong hình học. Để tính toán diện tích này, bạn cần nắm rõ công thức và quy trình thực hiện. Bài viết này sẽ cung cấp kiến thức và phương pháp giải bài tập liên quan đến diện tích hình quạt tròn, hỗ trợ bạn trong việc áp dụng vào thực tế và trong học tập.

Diện tích hình quạt tròn và các khái niệm cơ bản trong hình học

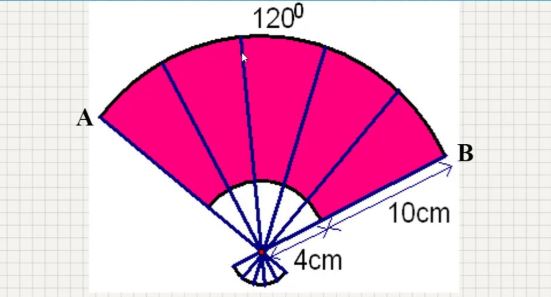
Hình quạt tròn là gì – một phần của hình tròn được giới hạn bởi hai bán kính và một cung tròn. Hình quạt tròn được tạo thành khi ta cắt một phần của hình tròn bằng hai đường thẳng đi qua tâm, tạo nên một góc ở tâm và một cung tròn tương ứng trên đường tròn.

Để tính diện tích hình quạt tròn, ta cần biết số đo góc ở tâm và bán kính của hình tròn. Công thức tính diện tích hình quạt tròn là: S = (α × π × R²)/360°, trong đó α là số đo góc ở tâm (tính bằng độ), R là bán kính và π ≈ 3,14. Công thức này dựa trên nguyên lý tỷ lệ thuận giữa diện tích và góc ở tâm.

Ví dụ thực tế về ứng dụng của hình quạt tròn có thể thấy trong thiết kế kiến trúc của Bảo tàng Louvre Abu Dhabi. Theo kiến trúc sư Jean Nouvel, mái vòm của công trình được thiết kế từ nhiều hình quạt tròn đan xen, tạo nên hiệu ứng ánh sáng độc đáo khi mặt trời chiếu qua các khoảng trống.

Trong thực tế, việc tính toán diện tích hình quạt tròn rất quan trọng trong nhiều lĩnh vực như xây dựng, thiết kế công nghiệp và nghệ thuật. Các kỹ sư thường sử dụng công thức này để tính toán diện tích các bộ phận máy móc có dạng hình quạt tròn hoặc thiết kế các cấu trúc kiến trúc phức tạp.

Công thức tính diện tích hình quạt tròn và các thành phần liên quan

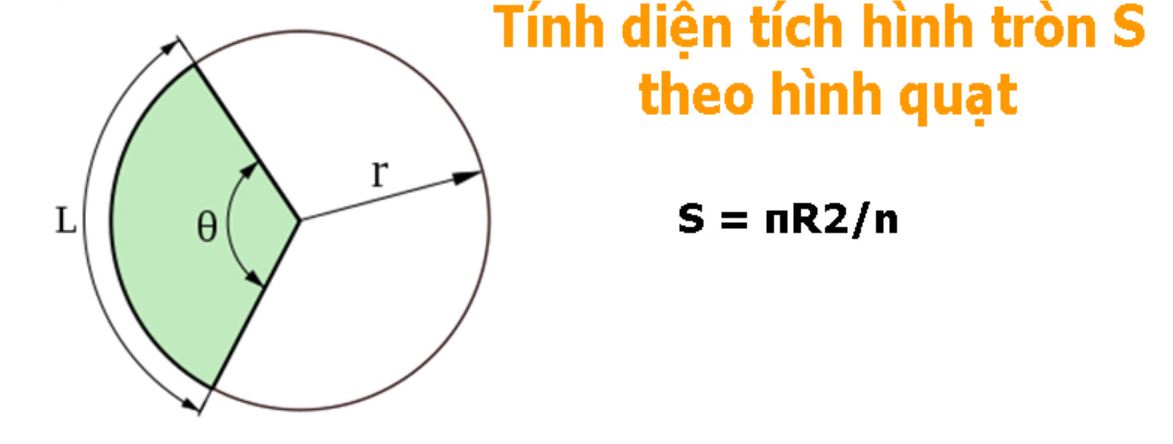
Công thức diện tích hình quạt được xác định dựa trên mối quan hệ giữa góc ở tâm và bán kính của hình tròn. Cụ thể, diện tích hình quạt tròn bằng tích của bình phương bán kính và số đo góc ở tâm (tính bằng radian), chia cho 2.

Để tính chính xác diện tích hình quạt tròn, ta cần nắm rõ công thức S = (R² × α)/2, trong đó R là bán kính và α là số đo góc ở tâm tính bằng radian. Việc chuyển đổi từ độ sang radian có thể thực hiện bằng cách nhân số đo góc với π/180.

Một yếu tố quan trọng khác cần xác định khi tính diện tích hình quạt là công thức tính độ dài cung tròn. Độ dài cung tròn và diện tích hình quạt có mối liên hệ mật thiết, giúp kiểm chứng tính chính xác của kết quả tính toán.

Khi áp dụng công thức, cần đặc biệt lưu ý đơn vị đo góc và bán kính phải thống nhất. Nếu bán kính được đo bằng centimeter thì kết quả diện tích sẽ có đơn vị là centimeter vuông. Điều này giúp tránh sai sót trong quá trình tính toán và đảm bảo độ chính xác của kết quả.

Phương pháp giải các dạng bài tập về diện tích hình quạt tròn

Để giải các bài tập về tính diện tích hình quạt, học sinh cần nắm vững công thức cơ bản S = (α/360°) × πR², trong đó α là số đo góc ở tâm và R là bán kính đường tròn. Việc áp dụng công thức này đòi hỏi sự chính xác trong tính toán và chuyển đổi đơn vị.

Ngoài ra, cần phân tích kỹ dữ kiện đề bài để xác định các yếu tố cần thiết. Đôi khi bài toán không cho trực tiếp góc ở tâm mà thông qua các quan hệ hình học khác, đòi hỏi phải vận dụng kiến thức về tam giác, tỷ số lượng giác để tìm ra.

Bài tập cơ bản về tính diện tích hình quạt tròn

Các bài tập cơ bản thường cho trực tiếp bán kính và góc ở tâm của hình quạt tròn. Ví dụ như bài toán: “Cho hình quạt tròn có bán kính 5cm và góc ở tâm 60°. Tính diện tích hình quạt tròn.”

Với những bài toán này, cách giải đơn giản là thay số vào công thức. Tuy nhiên, cần lưu ý đơn vị đo góc phải ở dạng độ và kiểm tra kỹ kết quả cuối cùng với đơn vị diện tích phù hợp.

Bài tập nâng cao và phương pháp giải

Các bài tập nâng cao về bài tập diện tích hình quạt thường kết hợp với các yếu tố hình học khác như đường cao, cung tròn hay dây cung. Phương pháp giải cần theo các bước:

• Vẽ hình minh họa chính xác
• Phân tích các quan hệ hình học
• Tìm các yếu tố chưa biết
• Áp dụng công thức tính diện tích

Việc giải các bài toán phức tạp đòi hỏi khả năng tư duy logic và kỹ năng phân tích tổng hợp tốt.

Các lỗi thường gặp khi giải bài tập

Khi giải toán về hình quạt tròn, học sinh thường mắc một số lỗi cơ bản. Lỗi phổ biến nhất là quên chuyển đổi đơn vị đo góc từ radian sang độ hoặc ngược lại. Điều này dẫn đến kết quả sai lệch đáng kể.

Một số học sinh cũng nhầm lẫn giữa diện tích hình quạt với diện tích cung tròn. Để tránh những sai sót này, cần đọc kỹ đề bài và kiểm tra lại các bước tính toán trước khi đưa ra kết quả cuối cùng.

Ngoài ra, việc không vẽ hình minh họa hoặc vẽ không chính xác cũng là nguyên nhân dẫn đến hiểu sai bài toán và giải sai. Vì vậy, cần dành thời gian để vẽ hình đầy đủ và chính xác ngay từ đầu.

Ứng dụng của diện tích hình quạt tròn trong toán học và thực tiễn

Diện tích hình quạt tròn có nhiều ứng dụng diện tích hình quạt quan trọng trong cả lĩnh vực toán học thuần túy và các ứng dụng thực tiễn. Việc nắm vững cách tính và ứng dụng của hình quạt tròn giúp giải quyết nhiều bài toán phức tạp trong hình học phẳng và không gian.

Ứng dụng trong các bài toán hình học phẳng

Trong hình học phẳng, diện tích hình quạt tròn thường được sử dụng để tính diện tích các phần của hình tròn khi biết góc ở tâm. Phương pháp này đặc biệt hữu ích khi giải các bài toán liên quan đến phân chia hình tròn thành các phần bằng nhau hoặc theo tỷ lệ cho trước.

Ngoài ra, diện tích hình quạt tròn còn được áp dụng trong việc tính toán diện tích các hình phức hợp được tạo thành từ nhiều hình quạt tròn ghép lại. Điều này thường xuất hiện trong các bài toán thiết kế mẫu hoa văn hình học hoặc trang trí nghệ thuật.

Ứng dụng trong các bài toán về khối tròn xoay

Khi nghiên cứu về tính thể tích khối tròn xoay, diện tích hình quạt tròn đóng vai trò quan trọng trong việc xác định diện tích xung quanh khối cầu​. Quá trình này liên quan đến việc xoay hình quạt tròn quanh một trục để tạo thành các mặt cong trong không gian ba chiều.

Việc hiểu rõ mối quan hệ giữa góc ở tâm và diện tích hình quạt tròn giúp giải quyết nhiều bài toán phức tạp về thể tích và diện tích xung quanh của các khối tròn xoay. Đây là kiến thức nền tảng cho việc học tập và nghiên cứu hình học không gian.

Ứng dụng thực tiễn của hình quạt tròn

Hình quạt tròn trong thực tế được ứng dụng rộng rãi trong nhiều lĩnh vực. Trong kiến trúc, hình quạt tròn được sử dụng để thiết kế mái vòm, cửa sổ hình quạt và các chi tiết trang trí. Các kỹ sư thường áp dụng tính chất của hình quạt tròn trong thiết kế cánh quạt máy bay, tuabin gió và các thiết bị quay khác.

Trong ngành công nghiệp sản xuất, hình quạt tròn được ứng dụng trong việc thiết kế các bộ phận chuyển động như bánh răng sector, cam phân đoạn. Các nhà thiết kế thời trang cũng sử dụng nguyên lý của hình quạt tròn để tạo ra những mẫu váy xòe, nếp gấp quạt độc đáo trên trang phục.

Mối liên hệ giữa diện tích hình quạt tròn với các khái niệm hình học khác

Diện tích hình quạt tròn có mối liên hệ mật thiết với nhiều khái niệm hình học khác, giúp giải quyết nhiều bài toán phức tạp. Việc hiểu rõ các mối liên hệ sẽ giúp vận dụng công thức tính diện tích hình quạt hiệu quả hơn trong thực tế.

Các mối liên hệ của diện tích hình quạt trong toán học thường được áp dụng trong việc tính toán diện tích các hình phẳng và khối trong không gian. Đây là kiến thức nền tảng quan trọng để giải quyết nhiều bài toán hình học phức tạp hơn.

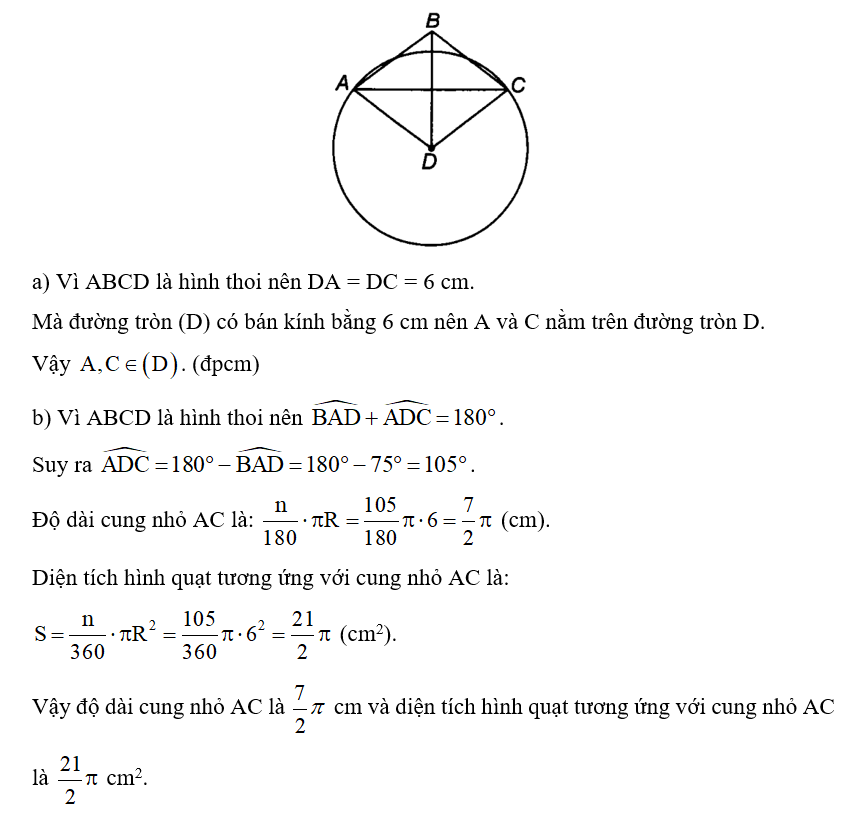
Liên hệ với diện tích hình tròn

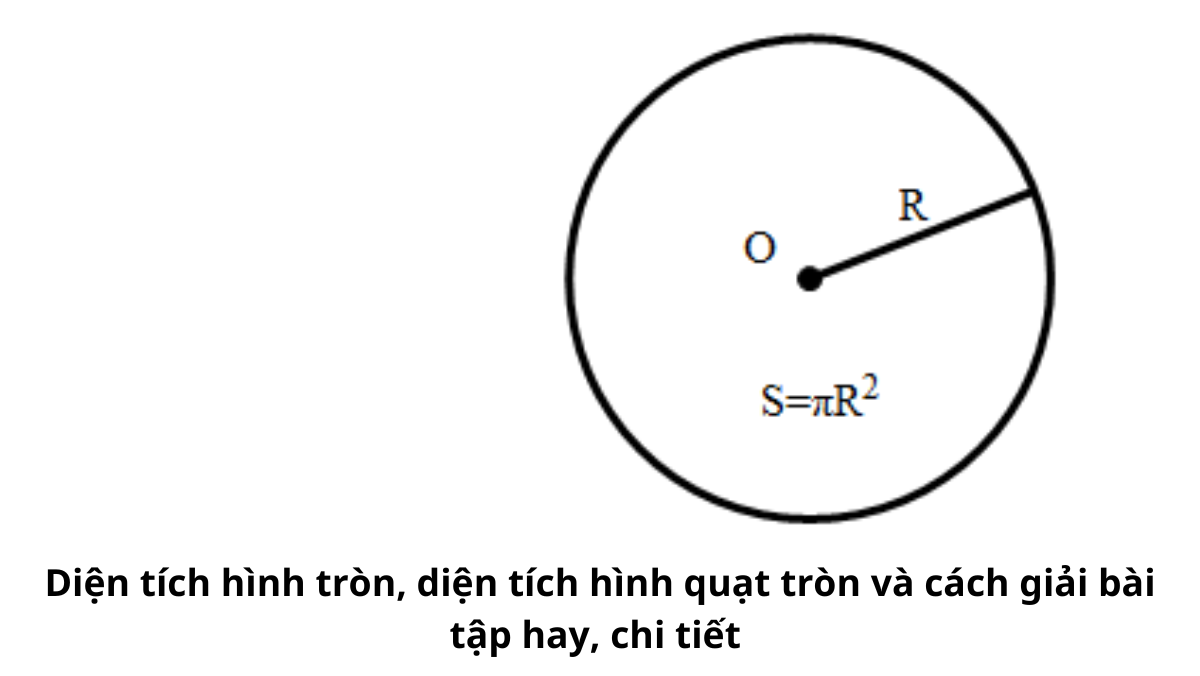
Diện tích hình quạt tròn có thể được xem như một phần của diện tích hình tròn, với tỷ lệ phụ thuộc vào số đo góc ở tâm. Khi góc ở tâm là 360 độ, diện tích hình quạt tròn chính bằng diện tích hình tròn.

Mối liên hệ này thể hiện qua công thức tính diện tích hình quạt tròn bằng tích của diện tích hình tròn và tỷ số giữa số đo góc ở tâm với 360 độ. Điều này cho thấy sự kết nối chặt chẽ giữa hai khái niệm hình học cơ bản này.

Liên hệ với diện tích các hình khối trong không gian

Trong không gian ba chiều, diện tích hình quạt tròn đóng vai trò quan trọng trong việc tính diện tích xung quanh lăng trụ và các hình khối khác. Ứng dụng thực tế có thể thấy trong kiến trúc, kỹ thuật và thiết kế công nghiệp.

Kiến thức về diện tích hình quạt tròn còn được áp dụng trong tính toán diện tích mặt cầu, nón và các hình khối có dạng xoay. Để tìm hiểu thêm về các ứng dụng của hình học, bạn có thể tham khảo thêm tại Trang web về toán.

Việc nắm vững mối liên hệ giữa diện tích hình quạt tròn với các hình khối trong không gian giúp giải quyết nhiều bài toán thực tế một cách hiệu quả và chính xác.

Khi tìm hiểu về diện tích hình quạt tròn, bạn sẽ khám phá nhiều khía cạnh thú vị từ định nghĩa cho đến công thức và ứng dụng trong thực tiễn. Bài viết đã cung cấp những phương pháp tính toán và bài tập đa dạng, giúp học sinh dễ dàng nắm bắt kiến thức toán học. Việc học tốt diện tích hình quạt không chỉ hỗ trợ trong việc giải bài tập mà còn mở ra cánh cửa ứng dụng thực tiễn đáng giá.