Diện tích mặt cầu hay diện tích xung quanh khối cầu là những kiến thức cơ bản mà học sinh cần phải thuộc lòng để có thể giải các bài toán hình học không gian. Trong bài viết này, cùng Hocthenao.vn tìm hiểu về cách tính diện tích xung quanh khối cầu, mối liên hệ giữa diện tích và thể tích của khối cầu cùng một số bài tập minh hoạ giúp bạn nắm vững được cách giải toán trong phần này.
Diện tích mặt cầu là gì?
Diện tích mặt cầu (hay còn gọi là diện tích xung quanh hình cầu) là diện tích bao phủ toàn bộ bề mặt bên ngoài của một hình cầu. Nó được tính bằng tổng diện tích của tất cả các phần vô cùng nhỏ trên bề mặt hình cầu.
Công thức tính diện tích mặt cầu có dạng như sau:
$$ S=4\mathrm{πR}^2 $$
Trong đó:
- S là diện tích mặt cầu
- π là số pi, có giá trị xấp xỉ 3,14159
- r là bán kính của mặt cầu
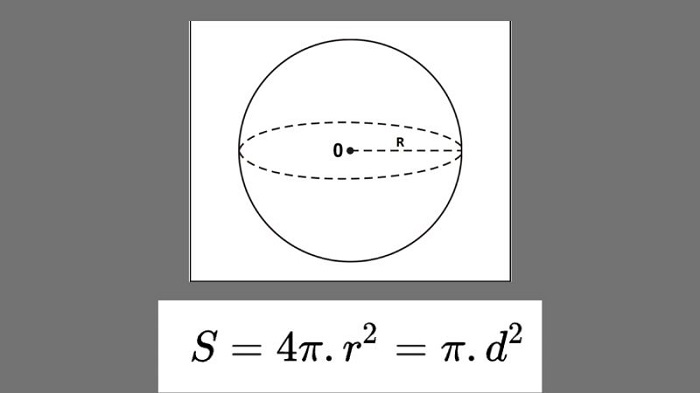
Công thức này dựa trên mối quan hệ giữa diện tích hình cầu và diện tích hình tròn lớn của mặt cầu đó. Diện tích xung quanh của hình cầu bằng 4 lần diện tích hình tròn lớn với bán kính hình cầu là yếu tố chính.
Ý nghĩa thực tiễn của diện tích xung quanh khối cầu
Diện tích xung quanh khối cầu không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng quan trọng trong thực tế. Nó đóng vai trò thiết yếu trong nhiều lĩnh vực khác nhau, từ khoa học kỹ thuật, sản xuất công nghiệp đến đời sống hàng ngày.
Ứng dụng trong khoa học kỹ thuật
Trong lĩnh vực khoa học kỹ thuật, diện tích xung quanh hình cầu có nhiều ứng dụng quan trọng như:
- Thiết kế và chế tạo các cấu trúc hình cầu: Diện tích xung quanh khối cầu được sử dụng để tính toán lượng vật liệu cần thiết cho việc xây dựng mái vòm, bể chứa, khoang tàu ngầm, hay các cấu trúc hình cầu khác. Việc tính toán chính xác diện tích giúp tối ưu hóa việc sử dụng vật liệu, tiết kiệm chi phí và đảm bảo độ an toàn cho công trình.
- Tính toán quỹ đạo chuyển động: Trong lĩnh vực vật lý và kỹ thuật hàng không, diện tích hình cầu được áp dụng để tính toán quỹ đạo chuyển động của các vật thể hình cầu giúp cho việc điều khiển hay định vị chúng trở nên hiệu quả, ví dụ như tên lửa, vệ tinh nhân tạo hay các phương tiện vũ trụ…
- Mô phỏng các hiện tượng vật lý: Cách tính Sxq hình cầu được sử dụng trong mô phỏng các hiện tượng vật lý liên quan đến sự truyền nhiệt, bức xạ hay khuếch tán.
Ứng dụng trong sản xuất công nghiệp
Công thức tính Sxq hình cầu được áp dụng cả trong lĩnh vực sản xuất công nghiệp như:
- Thiết kế và sản xuất các chi tiết hình cầu: Ta có thể tính toán lượng vật liệu cần thiết cho việc sản xuất các chi tiết hình cầu trong máy móc, thiết bị, hay các sản phẩm công nghiệp khác. Việc tính toán chính xác giúp tối ưu hóa việc sử dụng vật liệu, giảm thiểu phế liệu và nâng cao hiệu quả sản xuất.
- Lên kế hoạch sơn phủ hoặc mạ bề mặt: Người ta áp dụng công thức tính diện tích xung quanh khối cầu để tính toán lượng sơn, chất phủ hoặc kim loại cần thiết cho việc sơn phủ hoặc mạ bề mặt của các vật thể hình cầu một cách chính xác.
- Kiểm tra chất lượng sản phẩm: Kiểm tra độ chính xác về kích thước và hình dạng của các sản phẩm hình cầu. Việc so sánh diện tích thực tế với diện tích lý thuyết giúp phát hiện sai sót và đảm bảo chất lượng sản phẩm đạt yêu cầu.

Ứng dụng trong đời sống hàng ngày
Công thức tính diện tích xung quanh hình cầu còn được ứng dụng rất nhiều trong đời sống hàng ngày của chúng ta, chẳng hạn như:
- Tính toán diện tích bề mặt của các vật thể hình cầu: Tính toán diện tích bề mặt của các vật thể hình cầu trong đời sống hàng ngày, ví dụ như quả bóng rổ, quả bóng đá, hay quả địa cầu…
- Thiết kế đồ họa và mỹ thuật: Tạo ra các hình ảnh 3D chân thực cho các vật thể hình cầu. Việc áp dụng kiến thức hình học này giúp tạo ra những hình ảnh sống động và đẹp mắt.
- Giải trí và giáo dục: Được sử dụng trong các trò chơi và bài toán giải trí, giúp rèn luyện tư duy logic và khả năng giải quyết vấn đề. Việc học toán một cách thú vị thông qua các ứng dụng thực tế giúp kích thích niềm đam mê học tập và khơi dậy tiềm năng sáng tạo của trẻ.
Mối liên hệ giữa diện tích hình cầu và thể tích hình cầu
Diện tích hình cầu và thể tích hình cầu là hai đại lượng toán học có mối liên hệ chặt chẽ với nhau, thể hiện qua các công thức tính toán và ứng dụng thực tế.
Công thức tính toán:
- Diện tích mặt cầu: S = 4πr²
- Thể tích hình cầu: V = (4/3)πr³
Trong đó:
- S là diện tích mặt cầu
- V là thể tích hình cầu
- π là số pi, có giá trị xấp xỉ 3,14159
- r là bán kính của hình cầu

Từ hai công thức trên, ta có thể thấy mối liên hệ giữa diện tích mặt cầu và thể tích hình cầu như sau:
- Diện tích mặt cầu bằng 4 lần diện tích đáy của hình cầu.
- Thể tích hình cầu bằng 4/3 lần diện tích mặt cầu nhân với bán kính.
Bài tập có lời giải về tính diện tích mặt cầu
Dưới đây là một số bài tập có lời giải về tính diện tích mặt cầu giúp bạn nắm vững cách giải trong phần này:
Bài tập 1
Một quả cầu có bán kính 3cm. Tính diện tích xung quanh hình cầu.
Giải:
Diện tích xung quanh hình cầu được tính bằng công thức:
Sxq = 4πr²
Trong đó:
- S là diện tích mặt cầu
- π là số pi, có giá trị xấp xỉ 3,14159
- r là bán kính của hình cầu
Thay số vào công thức, ta được:
S = 4π * 3² = 36π (cm²)
Vậy diện tích mặt cầu là 36π cm².
Bài tập 2
Một bể chứa nước hình cầu có bán kính 2m. Để sơn toàn bộ bề mặt bên ngoài của bể, cần bao nhiêu lít sơn?
Giải:
Diện tích cần sơn chính là diện tích mặt cầu của bể chứa nước.
Diện tích xung quanh cầu được tính bằng công thức:
S = 4πr²
Thay số vào công thức, ta được:
S = 4π * 2² = 16π (m²)
Giả sử hệ số chuyển đổi là 1 (1m² sơn phủ được 1 lít diện tích), ta cần 16π lít sơn để sơn toàn bộ bề mặt bên ngoài của bể.
Vậy cần 16π lít sơn để sơn toàn bộ bề mặt bên ngoài của bể.
Bài tập 3
Một hình nón có bán kính đáy 5cm và chiều cao 12cm. Tính diện tích hình cầu ngoại tiếp hình nón.
Giải:
Bán kính của mặt cầu ngoại tiếp hình nón bằng đường sinh của hình nón, được tính bằng công thức:
l = √(r² + h²)
Trong đó:
- l là đường sinh của hình nón
- r là bán kính đáy của hình nón
- h là chiều cao của hình nón
Thay số vào công thức, ta được:
l = √(5² + 12²) = 13 cm
Bán kính hình cầu cầu ngoại tiếp hình nón bằng:
R = l = 13 cm
Diện tích hình cầu ngoại tiếp hình nón được tính bằng công thức:
S = 4πR²
Thay số vào công thức, ta được:
S = 4π * 13² = 676π (cm²)
Vậy diện tích hình cầu ngoại tiếp hình nón là 676π cm².
Bài tập 4
Một hình chóp tứ diện đều có cạnh đáy 6cm và chiều cao 4cm. Tính diện tích hình cầu nội tiếp hình chóp.
Giải:
Bán kính mặt cầu nội tiếp hình chóp tứ diện đều bằng 1/3 chiều cao của hình chóp, được tính bằng công thức:
r = h/3
Trong đó:
- r là bán kính mặt cầu nội tiếp
- h là chiều cao của hình chóp
Thay số vào công thức, ta được:
r = 4/3 = 1,33 cm
Diện tích hình cầu nội tiếp hình chóp được tính bằng công thức:
S = 4πr²
Thay số vào công thức, ta được:
S = 4π * 1,33² = 5,56π (cm²)
Vậy diện tích hình cầu nội tiếp hình chóp là 5,56π cm².
Bài tập 5
Một quả bóng rổ có đường kính 24cm. Tính diện tích xung quanh của quả bóng rổ.
Giải:
Bán kính của quả bóng rổ bằng một nửa đường kính, được tính bằng công thức:
r = d/2
Trong đó:
- r là bán kính của quả bóng rổ
- d là đường kính của quả bóng rổ
Thay số vào công thức, ta được:
r = 24/2 = 12 cm
Diện tích xung quanh của quả bóng rổ được tính bằng công thức:
S = 4πr²
Thay số vào công thức, ta được:
S = 4π * 12² = 576π (cm²)
Vậy diện tích xung quanh của quả bóng rổ là 576π cm².
Lời kết
Diện tích mặt cầu là một khái niệm quan trọng trong hình học không gian với nhiều ứng dụng thực tế. Việc nắm vững công thức tính toán và một vài bài tập minh họa sẽ giúp bạn giải quyết hiệu quả các bài toán liên quan đến hình cầu. Hãy luyện tập thường xuyên để thành thạo kiến thức này và chinh phục mọi thử thách hình học!




