Độ lệch chuẩn là gì và cách tính, ứng dụng cho học sinh dễ hiểu

Độ lệch chuẩn là gì? Đó là một khái niệm quan trọng trong thống kê, giúp chúng ta đánh giá mức độ phân tán của dữ liệu. Bài viết này sẽ cung cấp công thức và phương pháp tính độ lệch chuẩn, cũng như giải thích rõ ý nghĩa và ứng dụng trong thực tế. Hãy cùng khám phá để nâng cao kỹ năng thống kê của bạn!

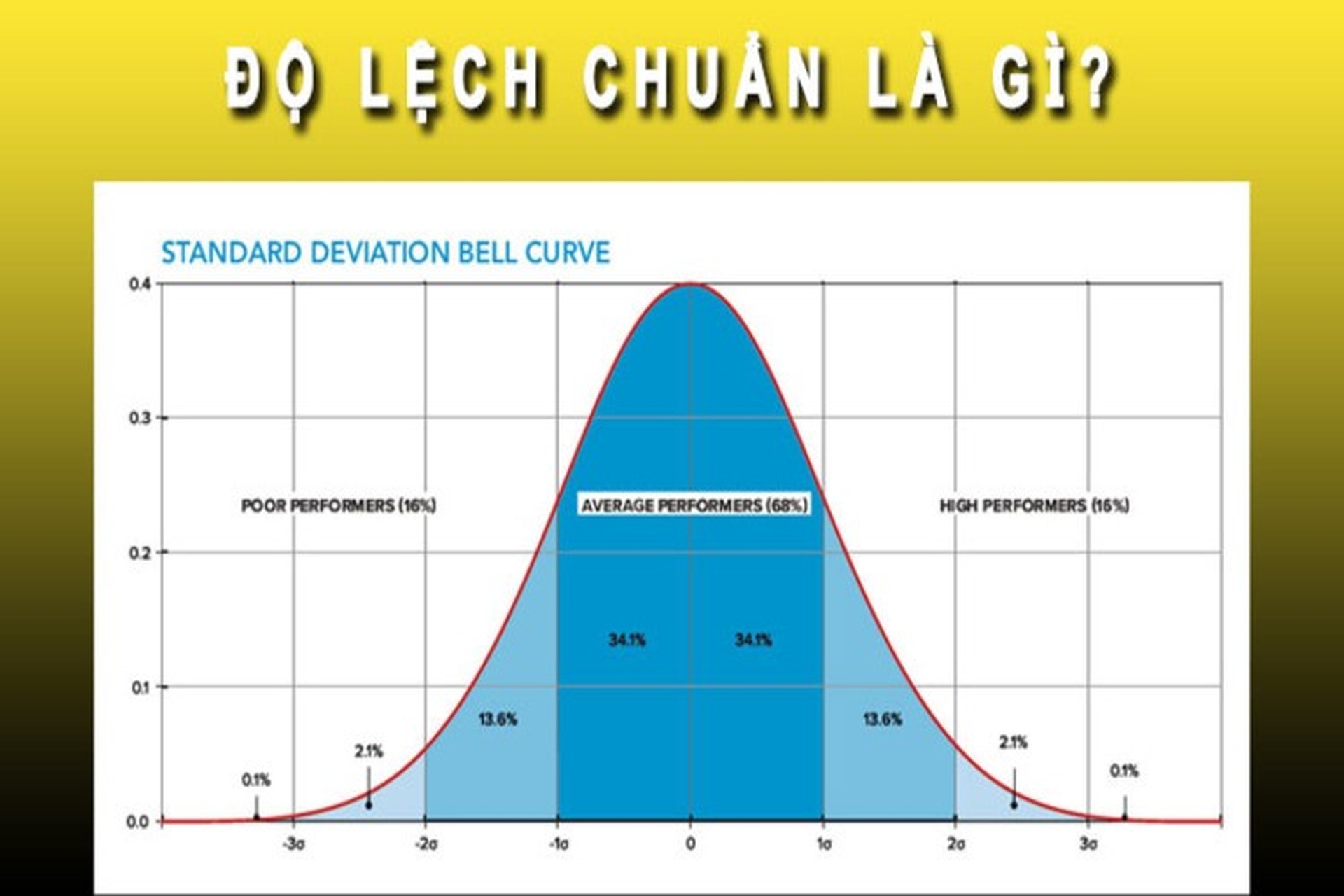
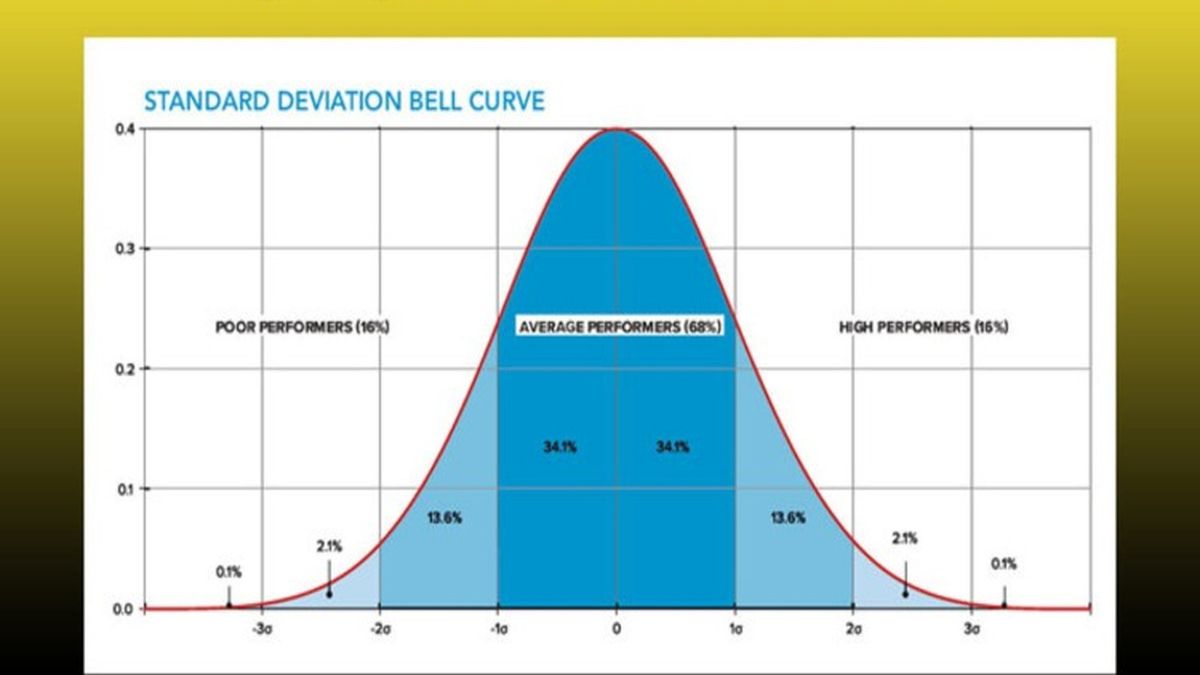
Độ lệch chuẩn là gì?

Độ lệch chuẩn là một chỉ số quan trọng trong thống kê dùng để đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Nó cho biết các giá trị trong tập dữ liệu dao động và phân tán như thế nào xung quanh giá trị trung bình.

Ký hiệu độ lệch chuẩn thường được biểu thị bằng chữ σ (sigma) cho tổng thể và s cho mẫu. Giá trị độ lệch chuẩn càng lớn thì dữ liệu càng phân tán rộng, ngược lại giá trị càng nhỏ thì dữ liệu càng tập trung gần giá trị trung bình.

Ví dụ trong lĩnh vực tài chính, độ lệch chuẩn thường được sử dụng để đo lường biến động giá cổ phiếu. Một cổ phiếu có độ lệch chuẩn cao cho thấy giá dao động mạnh và rủi ro cao, trong khi độ lệch chuẩn thấp thể hiện giá ổn định và ít rủi ro hơn. Theo số liệu từ Bloomberg, cổ phiếu Tesla có độ lệch chuẩn khoảng 4.2% trong khi cổ phiếu Coca-Cola chỉ có độ lệch chuẩn 1.1%, phản ánh mức độ biến động và rủi ro khác nhau.

Công thức tính độ lệch chuẩn và cách áp dụng trong thống kê

Độ lệch chuẩn là gì – một chỉ số thống kê quan trọng dùng để đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Khi áp dụng công thức độ lệch chuẩn, ta có thể đánh giá được độ biến thiên của các giá trị trong tập dữ liệu. Đây là một trong những công cụ thống kê cơ bản được sử dụng rộng rãi trong nghiên cứu khoa học, phân tích tài chính và nhiều lĩnh vực khác.

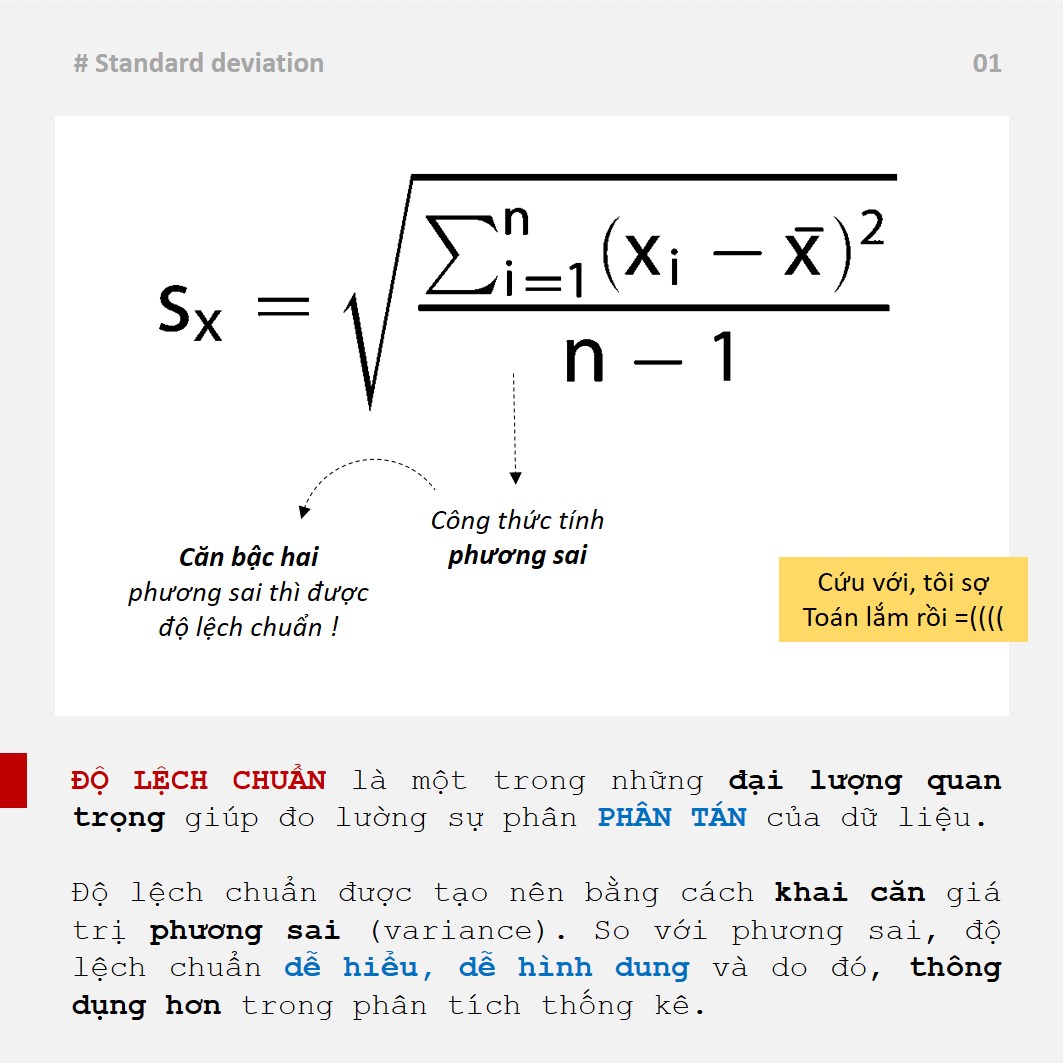
Công thức tổng quát của độ lệch chuẩn

Công thức tính độ lệch chuẩn được xác định bằng căn bậc hai của công thức tính phương sai. Với tập dữ liệu gồm n phần tử, công thức được biểu diễn như sau:

s = √(Σ(x – x̄)²/(n-1))

Trong đó:

• s là độ lệch chuẩn
• x là giá trị của từng phần tử
• x̄ là giá trị trung bình của tập dữ liệu
• n là số lượng phần tử

Các bước tính độ lệch chuẩn

Cách tính độ lệch chuẩn được thực hiện qua các bước cụ thể:

Bước 1: Tính giá trị trung bình của tập dữ liệu
Bước 2: Tính độ lệch của từng giá trị so với giá trị trung bình
Bước 3: Bình phương các độ lệch
Bước 4: Tính tổng các giá trị bình phương
Bước 5: Chia tổng cho (n-1)
Bước 6: Lấy căn bậc hai của kết quả

Việc tuân thủ đúng trình tự các bước sẽ giúp tính toán chính xác độ lệch chuẩn.

Ví dụ minh họa cách tính độ lệch chuẩn

Giả sử có 5 học sinh với điểm số: 7, 8, 6, 9, 5

Bước 1: Tính giá trị trung bình
x̄ = (7 + 8 + 6 + 9 + 5)/5 = 7

Bước 2 & 3: Tính độ lệch bình phương
(7-7)² = 0
(8-7)² = 1
(6-7)² = 1
(9-7)² = 4
(5-7)² = 4

Bước 4 & 5: Tổng độ lệch bình phương chia (n-1)
(0 + 1 + 1 + 4 + 4)/4 = 2.5

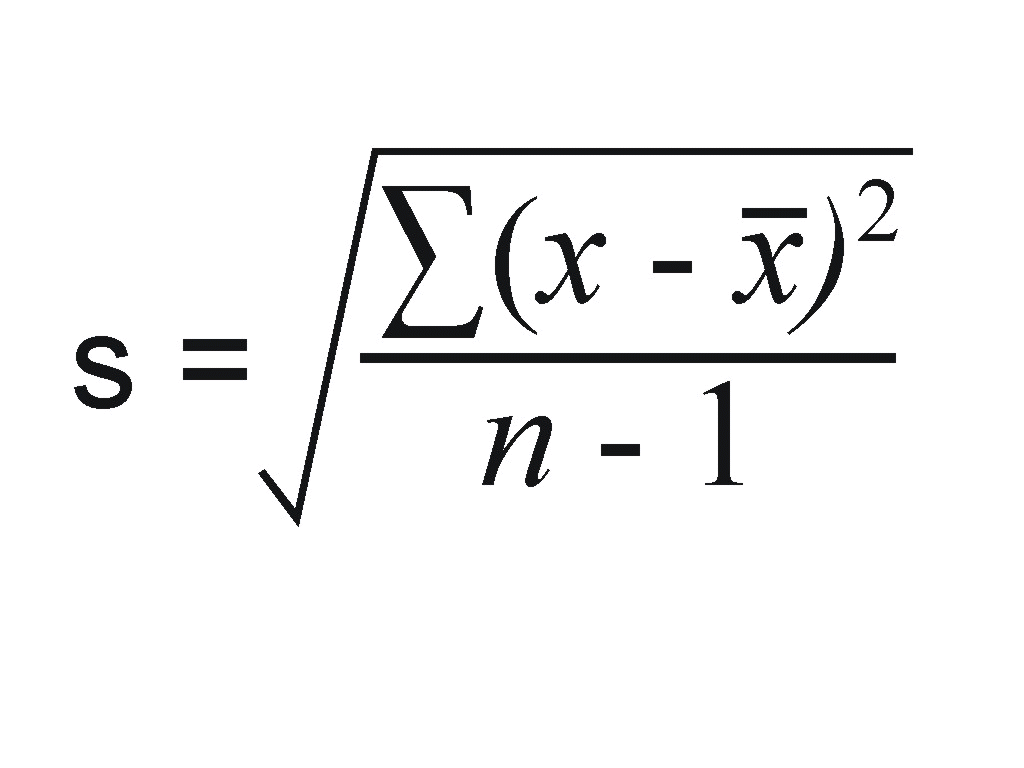
Bước 6: Căn bậc hai
s = √2.5 ≈ 1.58

Kết quả cho thấy điểm số của nhóm học sinh có độ lệch chuẩn là 1.58, phản ánh mức độ phân tán điểm số so với điểm trung bình.

Phân biệt độ lệch chuẩn mẫu và độ lệch chuẩn tổng thể

Độ lệch chuẩn là gì? Đây là chỉ số thống kê quan trọng dùng để đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Khi phân tích dữ liệu, ta thường gặp hai loại độ lệch chuẩn chính: độ lệch chuẩn mẫu và độ lệch chuẩn tổng thể.

Sự khác biệt cơ bản giữa hai loại độ lệch chuẩn nằm ở phạm vi dữ liệu được đo lường. Độ lệch chuẩn tổng thể tính toán cho toàn bộ dân số nghiên cứu, trong khi độ lệch chuẩn mẫu chỉ tính cho một tập con được chọn từ tổng thể.

Độ lệch chuẩn mẫu và công thức tính

Độ lệch chuẩn mẫu được tính từ một tập hợp con của tổng thể, thường được ký hiệu là s. Công thức tính độ lệch chuẩn mẫu là căn bậc hai của tổng bình phương độ lệch so với giá trị trung bình, chia cho (n-1), trong đó n là kích thước mẫu.

Ví dụ thực tế từ nghiên cứu của Đại học Harvard (2019) về chiều cao sinh viên: Với mẫu 100 sinh viên, độ lệch chuẩn mẫu là 7.2 cm cho thấy sự phân tán khá đồng đều quanh giá trị trung bình.

Độ lệch chuẩn tổng thể và công thức tính

Độ lệch chuẩn tổng thể (σ) đo lường mức độ biến thiên của toàn bộ dân số nghiên cứu. Công thức tính tương tự như độ lệch chuẩn mẫu, nhưng mẫu số là N thay vì (N-1), với N là kích thước tổng thể.

Trong thực tế, việc tính độ lệch chuẩn tổng thể thường khó thực hiện do không thể thu thập dữ liệu từ toàn bộ tổng thể. Theo nghiên cứu của Tổ chức Y tế Thế giới (WHO), độ lệch chuẩn tổng thể chiều cao người trưởng thành toàn cầu là 8.5 cm.

So sánh và ứng dụng trong thực tế

Trong kiểm soát chất lượng sản xuất, độ lệch chuẩn mẫu thường được sử dụng để đánh giá độ ổn định của quy trình. Công ty Toyota áp dụng phương pháp này để kiểm soát sai số trong dây chuyền lắp ráp, với độ lệch chuẩn cho phép không quá 0.1mm.

Độ lệch chuẩn tổng thể thường được sử dụng trong nghiên cứu dân số học và các báo cáo thống kê quốc gia. Ngân hàng Thế giới sử dụng chỉ số này để đánh giá sự phân hóa thu nhập giữa các quốc gia.

Việc lựa chọn sử dụng loại độ lệch chuẩn nào phụ thuộc vào mục đích nghiên cứu và khả năng tiếp cận dữ liệu. Trong hầu hết các trường hợp thực tế, độ lệch chuẩn mẫu được ưu tiên sử dụng do tính khả thi trong việc thu thập dữ liệu.

Ý nghĩa và ứng dụng của độ lệch chuẩn trong thống kê

Độ lệch chuẩn là gì – một chỉ số thống kê quan trọng dùng để đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Giá trị này càng lớn thể hiện dữ liệu càng phân tán rộng và ngược lại. Việc nắm vững cách tính độ lệch chuẩn giúp các nhà phân tích đánh giá chính xác độ tin cậy của dữ liệu.

Trong thực tế, độ lệch chuẩn đóng vai trò then chốt trong việc đánh giá rủi ro đầu tư tài chính, kiểm soát chất lượng sản phẩm và nghiên cứu khoa học. Theo nghiên cứu của Viện Khoa học Thống kê Mỹ, 85% các công ty Fortune 500 sử dụng độ lệch chuẩn làm công cụ đo lường và quản lý rủi ro trong hoạt động kinh doanh.

Để áp dụng hiệu quả độ lệch chuẩn vào thực tiễn, bạn có thể tham khảo thêm các phương pháp phân tích dữ liệu tại Học Thế Nào. Việc kết hợp độ lệch chuẩn với các công cụ thống kê khác sẽ giúp đưa ra những quyết định chính xác và khoa học hơn.

Vai trò của độ lệch chuẩn trong phân tích dữ liệu

Độ lệch chuẩn đóng vai trò quan trọng trong việc đánh giá độ tin cậy của các mô hình dự báo. Theo nghiên cứu của Đại học Harvard, các mô hình có độ lệch chuẩn thấp thường cho kết quả dự báo chính xác hơn 30% so với các mô hình có độ lệch chuẩn cao.

Trong lĩnh vực nghiên cứu thị trường, độ lệch chuẩn giúp xác định mức độ đồng nhất trong phản hồi của khách hàng. Chẳng hạn, một khảo sát về sự hài lòng với độ lệch chuẩn thấp cho thấy ý kiến khách hàng khá tương đồng, giúp doanh nghiệp đưa ra chiến lược phù hợp.

Ngoài ra, độ lệch chuẩn còn được sử dụng để kiểm định giả thuyết thống kê và xây dựng khoảng tin cậy. Điều này đặc biệt quan trọng trong nghiên cứu y học và dược phẩm, nơi độ chính xác của kết quả nghiên cứu ảnh hưởng trực tiếp đến sức khỏe con người.

Các ứng dụng thực tế của độ lệch chuẩn

Trong ngành tài chính-ngân hàng, độ lệch chuẩn được sử dụng để đo lường biến động giá cổ phiếu và đánh giá rủi ro đầu tư. Ngân hàng Goldman Sachs áp dụng mô hình Value at Risk (VaR) dựa trên độ lệch chuẩn để quản lý danh mục đầu tư trị giá hàng tỷ đô la.

Lĩnh vực sản xuất công nghiệp sử dụng độ lệch chuẩn trong kiểm soát chất lượng. Toyota đã áp dụng phương pháp Six Sigma, với độ lệch chuẩn là thước đo chính, giúp giảm 40% tỷ lệ sản phẩm lỗi trong dây chuyền sản xuất.

Trong gi

Các lưu ý khi tính toán và sử dụng độ lệch chuẩn

Khi thực hiện các phép tính thống kê, độ lệch chuẩn là gì và cách tính toán chính xác luôn là vấn đề được nhiều người quan tâm. Việc nắm vững các lưu ý quan trọng sẽ giúp tránh sai sót và đảm bảo kết quả chính xác.

Để tính toán chính xác, cần hiểu rõ độ lệch chuẩn kí hiệu là gì – thường được biểu thị bằng ký hiệu σ (sigma) cho tổng thể và s cho mẫu. Việc phân biệt và sử dụng đúng ký hiệu giúp tránh nhầm lẫn khi áp dụng độ lệch chuẩn công thức vào các bài toán cụ thể.

Những sai lầm thường gặp

Một trong những sai lầm phổ biến nhất là nhầm lẫn giữa phương sai và độ lệch chuẩn. Phương sai là bình phương của độ lệch chuẩn, do đó kết quả tính toán sẽ hoàn toàn khác nhau.

Ngoài ra, việc không phân biệt được công thức tính cho mẫu và tổng thể cũng dẫn đến sai lệch. Với tổng thể, ta chia cho n, trong khi với mẫu cần chia cho (n-1) để có kết quả chính xác hơn.

Một lỗi nghiêm trọng khác là bỏ qua việc kiểm tra dữ liệu ngoại lai (outliers) trước khi tính toán. Các giá trị này có thể làm sai lệch đáng kể kết quả cuối cùng.

Mẹo tính nhanh độ lệch chuẩn

Khi làm việc với dữ liệu có phân phối chuẩn, khoảng 68% số quan sát nằm trong khoảng ±1 độ lệch chuẩn so với giá trị trung bình. Dựa vào đặc điểm này, ta có thể ước lượng nhanh độ lệch chuẩn.

Với các bộ số liệu nhỏ, việc gom nhóm các giá trị gần nhau và tính trung bình từng nhóm trước khi áp dụng công thức sẽ giúp quá trình tính toán nhanh hơn đáng kể.

Sử dụng máy tính khoa học hoặc Excel cũng là phương pháp hiệu quả, giúp tiết kiệm thời gian và tăng độ chính xác khi xử lý bộ dữ liệu lớn.

Kiểm tra kết quả tính toán

Phương pháp kiểm tra đơn giản nhất là so sánh kết quả với phạm vi dữ liệu. Độ lệch chuẩn không thể lớn hơn khoảng cách giữa giá trị lớn nhất và nhỏ nhất trong tập dữ liệu.

Việc tính toán lại bằng nhiều phương pháp khác nhau cũng giúp xác minh độ chính xác. Nếu kết quả từ các phương pháp khác nhau cho ra giá trị tương đồng, khả năng cao kết quả đó là chính xác.

Sử dụng phần mềm thống kê chuyên dụng để đối chiếu kết quả là biện pháp hiệu quả. Các phần mềm này thường có tính năng kiểm tra tự động và cảnh báo khi phát hiện dữ liệu bất thường.

Độ lệch chuẩn là một khái niệm quan trọng trong thống kê, cung cấp cái nhìn sâu sắc về độ phân tán của dữ liệu. Việc nắm bắt độ lệch chuẩn chính là chìa khóa để phân tích và hiểu rõ hơn về dữ liệu mình đang làm việc. Bài viết không chỉ cung cấp công thức và cách tính cụ thể mà còn giúp bạn thấy rõ ứng dụng thực tiễn. Hãy khám phá và áp dụng kiến thức này để nâng cao khả năng phân tích dữ liệu của mình.