Xác định đường cao hình tam giác cân là việc làm cơ bản để tính toán được diện tích của hình hay những yêu cầu liên quan khác. Để tìm ra đường cao nhanh nhất, ta có thể áp dụng những tính chất của tam giác cân. Hãy theo dõi ngay bài viết dưới đây để nắm bắt các thông tin chi tiết.
Tính chất đường cao hình tam giác cân
Tam giác cân là dạng hình tam giác và có hai cạnh bên bằng nhau, đồng thời hai góc bằng nhau. Do đó đường cao hình tam giác cân sẽ có một số tính chất cơ bản và tính chất đặc biệt. Cụ thể như sau:
Tính chất cơ bản
- Đường cao của hình tam giác cân hạ từ đỉnh vuông góc với cạnh đáy cũng sẽ là đường trung tuyến của tam giác, do đó giao của đường cao và cạnh đáy chính là trung điểm của cạnh đáy.
- Đường cao tam giác đồng thời cũng là đường trung trực và đường phân giác của góc đỉnh. Đây cũng là đường chia tam giác cân thành hai hình bằng nhau.
Xem thêm: Hình tam giác cân là gì? Đặc điểm của tam giác cân
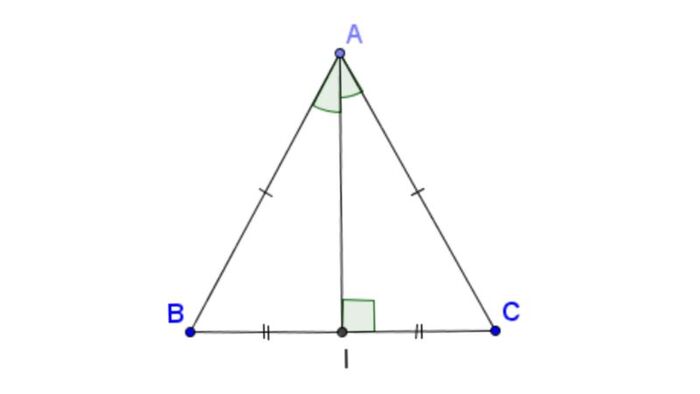
Tính chất toán học
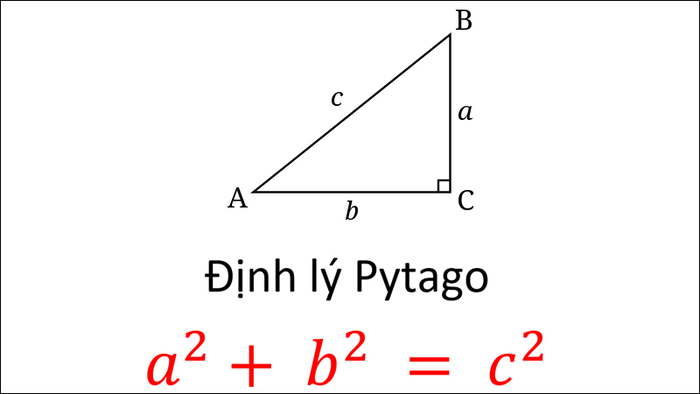
Vì đường cao của tam giác cân hạ từ đỉnh sẽ phân chia hình đó thành 2 tam giác con bằng nhau nên ta có thể áp dụng định lý Pythagoras để tính toán chiều cao. Cụ thể:
$${h=\sqrt{\left[a^2-\left(\frac b2\right)^2\right]}}$$
Với h là chiều cao, a là độ dài cạnh bên, b là độ dài cạnh đáy.
Xem thêm: Các dấu hiệu nhận biết hình tam giác cân
Công thức tính đường cao tam giác cân
Với một hình tam giác cân có độ dài cạnh bên là a, độ dài cạnh đáy là b, chiều cao là h, ta sẽ áp dụng được định lý Pythagoras để tính được chiều cao:
$$a^2=\left(\frac b2\right)^2+h^2$$
$$Suy\;ra\;h^2=\;a^2\;-\;\left(\frac b2\right)^2$$
$$h\;=\;\sqrt{\left[a^2-\left(\frac b2\right)^2\right]}$$
Như vậy có thể kết luận rằng bất kỳ một tam giác cân nào cũng có chiều cao hạ từ đỉnh xuống cạnh đáy bằng căn bậc hai của độ dài cạnh bên mũ hai trừ đi độ dài cạnh đáy chia hai mũ hai.
Xem thêm: Ứng dụng đường cao tính diện tích tgc
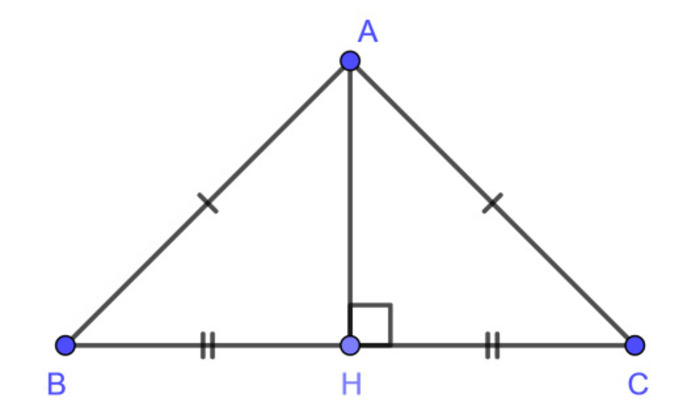
Các bước tính đường cao trong tam giác cân
Quy trình tính đường cao trong tam giác cân như sau:
- Bước 1: Xem xét đề bài để xác định câu hỏi cần trả lời, đồng thời có sự chuẩn bị cần thiết.
- Bước 2: Xác định cạnh đáy và đỉnh của hình tgc với cạnh đáy sẽ có độ dài khác với hai cạnh còn lại.
- Bước 3: Từ đỉnh hạ đường thẳng vuông góc với cạnh đáy. Ta sẽ có đường cao là đoạn từ đỉnh và giao điểm của hai đường.
- Bước 4: Áp dụng định lý Pythagoras với công thức
$$h\;=\;\sqrt{\left[a^2-\left(\frac b2\right)^2\right]}$$
Từ đó tìm ra được chiều cao của tam giác đề bài đã cho.
Bài tập ví dụ tính đường cao tam giác cân
Để nắm bắt công thức và cách tính đường cao tam giác cân nhanh và hiệu quả nhất, hãy xét một ví dụ minh hoạ như sau:
Ví dụ 1: Cho hình tgc bất kỳ với hai cạnh bên có chiều dài là 6cm, cạnh đáy là 8cm. Độ dài chiều cao và diện tích của hình tam giác cân đó là bao nhiêu?
Lời giải
Áp dụng công thức tính đường cao trong tam giác cân là h = √[a2 – (b/2)2]
Ta có chiều cao của hình tam giác đã cho là h = √[62 – (8/2)2] = √20 = 4,47cm
Diện tích của hình tam giác là S = b x h = 6 x 4,47 = 26,82 cm2
Ví dụ 2: Cho hình tam giác ABC cân tại A. Chiều cao AH là 2cm và độ dài cạnh đáy BC bằng 6cm. Hãy tính độ dài của đoạn AC.
Lời giải
Theo tính chất, ta có chiều cao của tgc cũng chính là đường trung tuyến của tgc. Suy ra H là trung điểm của đoạn BC. Đề bài cho BC = 6cm nên HC = 3cm.
Lúc này AC là độ dài cạnh huyền của tam giác AHC, do đó
AC = √(AH2 + HC2) = √(32 + 22) = 4cm.
Xem thêm: Công thức tính chu vi hình tam giác cân
Ứng dụng của đường cao trong thực tế
Đường cao của một hình tam giác cân được áp dụng rất nhiều trong thực tiễn các ngành nghề như sau:
- Đối với ngành kỹ thuật: Rất nhiều công trình như nhà ở, cầu cống,… được xác định chiều cao hoặc phân tích điểm đặt lực phù hợp nhờ vào công thức tính đường cao của tam giác. Từ đó các công trình luôn đảm bảo được sự chắc chắn, bền bỉ và an toàn khi sử dụng.
- Đối với ngành thiết kế: Bố cục hài hoà là yếu tố quan trọng được đặt lên hàng đầu trong thiết kế, hội hoạ, kiến trúc. Dạng hình tam giác cân luôn được sử dụng rộng rãi để tạo khung cho những tác phẩm này.
- Đối với ngành giáo dục: Tam giác là một hình toán học quan trọng. Đây là một dạng hình cơ bản, giúp học sinh nhận diện. Đồng thời, tam giác cân và đường cao của nó cũng được sử dụng để tính toán thông số và ứng dụng được vào trong thực tiễn.

Trên đây là những thông tin chi tiết về cách xác định, tính chất và cách tính đường cao hình tam giác cân. Đây đều là những kiến thức cần thiết trong tất cả các lĩnh vực đời sống. Đừng quên bình luận hoặc nhắn tin ngay cho Học thế nào nếu bạn còn cần giải đáp những thắc mắc khác!




