Dương cộng âm ra gì và quy tắc tính toán số âm số dương hiệu quả

Dương cộng âm ra gì? Đây là câu hỏi quan trọng trong toán học, giúp hiểu rõ hơn về phép tính với số âm và số dương. Bài viết này sẽ cung cấp kiến thức cơ bản, quy tắc tính toán và nhiều ví dụ minh họa. Tham khảo để nâng cao kỹ năng toán học và áp dụng vào thực tế một cách hiệu quả.

Dương cộng âm ra gì?

Khi thực hiện phép tính dương cộng âm ra gì, kết quả sẽ phụ thuộc vào giá trị tuyệt đối của hai số. Nếu số dương có giá trị tuyệt đối lớn hơn số âm, kết quả sẽ là một số dương. Ngược lại, nếu số âm có giá trị tuyệt đối lớn hơn số dương, kết quả sẽ là một số âm.

Ví dụ cụ thể, khi cộng số dương 5 với số âm -3, ta có 5 + (-3) = 2, kết quả là số dương vì |5| > |-3|. Tuy nhiên, nếu cộng số dương 4 với số âm -7, ta có 4 + (-7) = -3, kết quả là số âm do |-7| > |4|.

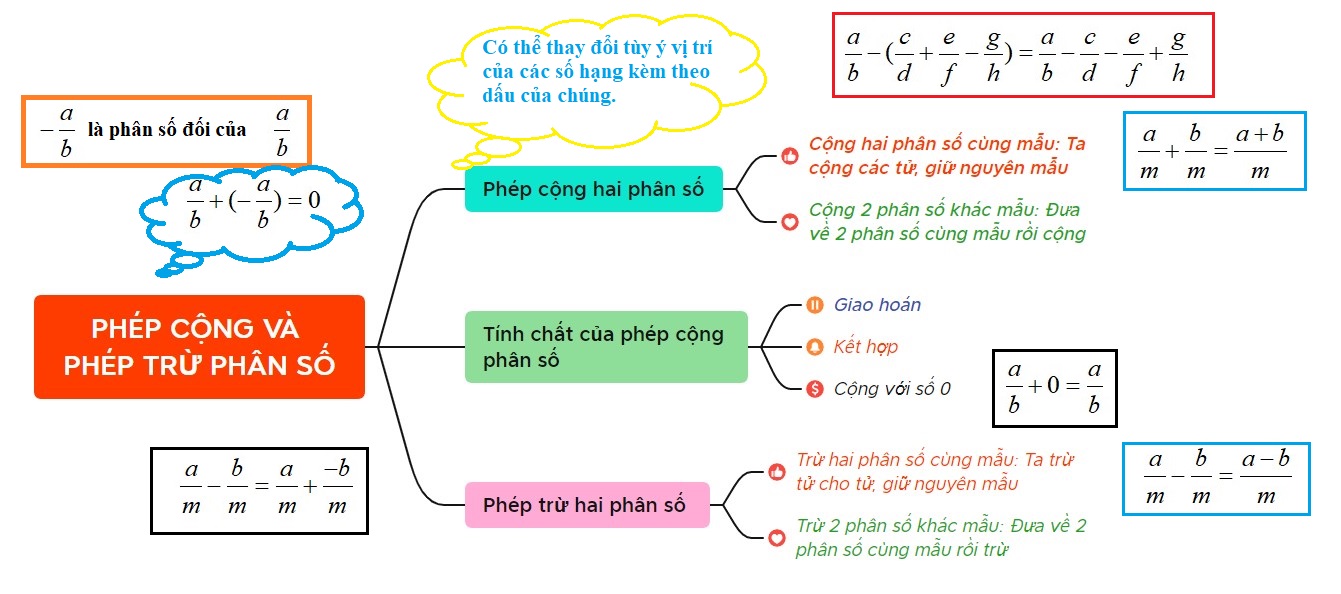
Quy tắc này áp dụng cho mọi trường hợp cộng số dương với số âm trong toán học. Việc so sánh giá trị tuyệt đối giữa hai số sẽ giúp xác định dấu của kết quả một cách nhanh chóng và chính xác. Đây là kiến thức cơ bản quan trọng trong phép tính với số nguyên.

Các quy tắc cơ bản về phép tính với số âm và số dương

Phép tính giữa số âm và số dương là một trong những kiến thức toán học cơ bản quan trọng. Việc nắm vững các quy tắc này giúp giải quyết nhiều bài toán phức tạp hơn. Các phép tính cơ bản bao gồm cộng và trừ giữa số âm với số dương.

Phép cộng giữa số âm và số dương

Khi thực hiện phép cộng giữa số âm và số dương, kết quả phụ thuộc vào giá trị tuyệt đối của hai số. Âm cộng dương bằng gì phụ thuộc vào số nào có giá trị tuyệt đối lớn hơn. Nếu giá trị tuyệt đối của số âm lớn hơn, kết quả là số âm. Ngược lại, nếu giá trị tuyệt đối của số dương lớn hơn, kết quả là số dương.

Âm + dương ra gì có thể hiểu đơn giản như việc so sánh độ lớn của hai lực đẩy ngược chiều nhau. Ví dụ như âm nhân dương ra gì, phép cộng cũng tuân theo quy tắc tương tự về việc xét giá trị tuyệt đối của các số.

Phép trừ giữa số âm và số dương

Dương trừ âm bằng gì được xác định bằng cách chuyển phép trừ thành phép cộng với số đối của số bị trừ. Khi trừ một số âm, ta cộng với số dương tương ứng. Điều này làm cho kết quả luôn là một số dương và có giá trị lớn hơn số bị trừ ban đầu.

Số âm trừ số dương ra gì cũng áp dụng nguyên tắc chuyển đổi tương tự. Khi số âm trừ đi một số dương, kết quả sẽ là một số âm có giá trị tuyệt đối bằng tổng giá trị tuyệt đối của hai số ban đầu.

Ví dụ minh họa các phép tính

Phép cộng số âm với số dương:
(-5) + 3 = -2 (vì |-5| > |3|)
(-4) + 7 = 3 (vì |-4| < |7|)

Phép trừ số âm với số dương:
5 – (-3) = 5 + 3 = 8
(-6) – 4 = (-6) + (-4) = -10

Các ví dụ trên minh họa rõ ràng cách áp dụng quy tắc tính toán giữa số âm và số dương. Việc thực hành nhiều sẽ giúp nắm vững và vận dụng thành thạo các quy tắc này.

Phương pháp nhận biết và phân biệt số âm số dương trên trục số

Việc phân biệt số âm và số dương là một kỹ năng toán học cơ bản nhưng rất quan trọng. Khi đặt câu hỏi “dương cộng âm ra gì“, ta cần hiểu rõ bản chất và vị trí của chúng trên trục số để tính toán chính xác.

Để cách phân biệt dương và âm được rõ ràng, cần nắm vững các quy tắc cơ bản về vị trí và đặc điểm của chúng. Việc phân biệt này sẽ giúp giải quyết nhiều bài toán phức tạp hơn trong tương lai.

Vị trí của số âm và số dương trên trục số

Trên trục số, điểm 0 đóng vai trò như một ranh giới phân chia hai miền số. Các số nằm bên phải số 0 được gọi là số dương, thường được đánh dấu bằng dấu “+”. Ngược lại, các số nằm bên trái số 0 là số âm và được đánh dấu bằng dấu “-“.

Khoảng cách từ một số đến điểm 0 thể hiện giá trị tuyệt đối của số đó. Ví dụ, số -3 và số 3 có cùng khoảng cách đến 0 là 3 đơn vị, nhưng nằm ở hai phía đối diện của trục số.

Các đặc điểm nhận dạng số âm và số dương

Số dương luôn lớn hơn 0 và thường được viết không kèm dấu. Chẳng hạn như 1, 2, 3 là các số dương. Khi cần nhấn mạnh, ta có thể thêm dấu “+” phía trước như +1, +2, +3.

Số âm luôn nhỏ hơn 0 và bắt buộc phải có dấu “-” phía trước. Ví dụ: -1, -2, -3. Điều đặc biệt là khi so sánh các số âm, số có giá trị tuyệt đối lớn hơn sẽ nhỏ hơn. Như -5 nhỏ hơn -3 dù |5| > |3|.

Bài tập thực hành và ứng dụng

Để rèn luyện khả năng nhận biết số âm số dương, có thể thực hành qua các bài tập đơn giản:

• So sánh các cặp số: -2 và 3; -5 và -1; 0 và -4
• Sắp xếp dãy số theo thứ tự tăng dần: 2, -3, 0, 5, -1
• Tính tổng các cặp số đối: (-2) + 2; (-5) + 5

Việc thực hành thường xuyên sẽ giúp nâng cao khả năng tính toán với số âm và số dương trong các bài toán phức tạp hơn.

Ứng dụng của số âm và số dương trong thực tế

Số âm và số dương có vai trò quan trọng trong việc biểu diễn các đại lượng trái dấu nhau. Hiểu được dương âm là gì giúp chúng ta dễ dàng mô tả các hiện tượng đối lập trong tự nhiên và đời sống. Việc nắm vững các phép tính với số âm và số dương là nền tảng để giải quyết nhiều bài toán thực tế.

Biểu diễn nhiệt độ và độ cao

Nhiệt độ là một trong những ví dụ về dương và âm điển hình nhất. Khi nhiệt kế hiển thị 5°C, đó là nhiệt độ dương, còn -3°C là nhiệt độ âm. Tương tự với độ cao, các địa điểm trên mực nước biển được tính bằng số dương, còn dưới mực nước biển được tính bằng số âm.

Các nhà khí tượng thường sử dụng số âm và số dương để ghi nhận sự thay đổi nhiệt độ theo thời gian. Việc theo dõi biến động này giúp dự báo thời tiết chính xác hơn và cảnh báo sớm các hiện tượng thời tiết cực đoan.

Thể hiện lãi lỗ trong kinh doanh

Trong kế toán và tài chính, dương cộng âm là gì thường được áp dụng để tính toán lãi lỗ. Số dương thể hiện lợi nhuận, trong khi số âm biểu thị khoản lỗ. Ví dụ, một cửa hàng có doanh thu +5 triệu và chi phí -3 triệu, lợi nhuận sẽ là +2 triệu đồng.

Các ngân hàng sử dụng số âm để thể hiện số dư tài khoản bị thấu chi. Khi khách hàng rút tiền nhiều hơn số dư hiện có, tài khoản sẽ hiển thị số âm, cho biết khoản nợ cần thanh toán với ngân hàng.

Ứng dụng trong khoa học kỹ thuật

Trong vật lý, điện tích dương và âm là cơ sở để giải thích nhiều hiện tượng điện từ. Các kỹ sư điện sử dụng khái niệm này để thiết kế mạch điện và các thiết bị điện tử.

Trong xây dựng, số âm và số dương giúp xác định chính xác vị trí các cấu kiện. Ví dụ, khi thiết kế móng nhà, độ sâu được tính bằng số âm, còn chiều cao tầng được tính bằng số dương. Theo Hiệp hội Kỹ sư Xây dựng Việt Nam, việc áp dụng hệ thống tọa độ này giúp giảm thiểu sai sót trong thi công và nâng cao chất lượng công trình.

Khái niệm âm dương trong các lĩnh vực khác

Nguyên lý âm dương không chỉ tồn tại trong triết học phương Đông mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của đời sống. Sự cân bằng giữa hai yếu tố đối lập này tạo nên sự hài hòa và phát triển trong tự nhiên cũng như xã hội.

Âm dương trong âm nhạc

Trong âm nhạc, âm trầm là gì được hiểu là những nốt nhạc có tần số thấp, tạo cảm giác sâu lắng, trầm ấm. Ngược lại, các nốt cao tạo cảm giác sáng sủa, nhẹ nhàng. Sự kết hợp giữa dương âm trong âm nhạc tạo nên những giai điệu đa dạng, phong phú.

Các nhạc sĩ thường sử dụng sự tương phản giữa âm trầm và âm cao để tạo hiệu ứng cảm xúc trong tác phẩm. Ví dụ như trong bản giao hưởng số 5 của Beethoven, phần mở đầu sử dụng âm trầm để tạo không khí u ám, sau đó chuyển sang âm cao mang lại cảm giác hy vọng, sáng sủa.

Nguyên lý âm dương trong khoa học tự nhiên

Nguyên lý dương âm được thể hiện rõ nét trong nhiều hiện tượng tự nhiên như điện tử và lỗ trống trong vật lý bán dẫn, proton và electron trong cấu tạo nguyên tử. Trong sinh học, sự cân bằng âm dương thể hiện qua quá trình trao đổi chất, hô hấp và quang hợp của sinh vật.

Các nhà khoa học tại Viện Vật lý Kỹ thuật Trung Quốc đã chứng minh rằng nguyên lý âm dương có thể giải thích nhiều hiện tượng trong vũ trụ như sự hình thành các cặp hạt và phản hạt, hay sự cân bằng giữa vật chất và phản vật chất.

Ứng dụng nguyên lý âm dương trong đời sống

Dương âm và ứng dụng trong đời sống được thể hiện qua nhiều lĩnh vực như kiến trúc, thiết kế nội thất và y học. Trong kiến trúc, việc kết hợp không gian mở (dương) và đóng (âm) tạo nên sự cân bằng và hài hòa cho công trình.

Trong y học cổ truyền, nguyên lý âm dương được áp dụng để chẩn đoán và điều trị bệnh. Bác sĩ Nguyễn Văn A, chuyên gia y học cổ truyền tại Bệnh viện Y học cổ truyền Trung ương cho biết: “Việc điều trị dựa trên nguyên tắc cân bằng âm dương giúp phục hồi trạng thái khỏe mạnh cho cơ thể.”

Nguyên lý này còn được ứng dụng trong phong thủy để tạo không gian sống hài hòa. Sự kết hợp giữa các yếu tố như màu sắc, ánh sáng và bố trí nội thất theo nguyên tắc âm dương giúp tạo ra môi trường sống thoải mái và thuận lợi.

Các bài tập và phương pháp giải về phép tính với số âm số dương

Phép tính với số âm và số dương là một trong những kiến thức toán học cơ bản nhưng rất quan trọng. Việc nắm vững các quy tắc tính toán sẽ giúp học sinh giải quyết được nhiều bài toán phức tạp hơn trong chương trình học.

Khi thực hiện phép tính giữa số âm và số dương, cần tuân theo các quy tắc cụ thể. Ví dụ khi dương cộng âm ra gì thì kết quả sẽ phụ thuộc vào giá trị tuyệt đối của các số. Nếu số dương lớn hơn giá trị tuyệt đối của số âm, kết quả là số dương và ngược lại.

Bài tập cơ bản về phép cộng trừ

Để thực hành phép tính với số âm và dương, học sinh cần làm nhiều bài tập đa dạng. Các dạng bài tập cơ bản thường bắt đầu với phép cộng hai số đơn giản như âm cộng dương.

Khi giải các bài tập này, cần chú ý đến dấu của các số và thứ tự thực hiện phép tính. Việc làm chủ các bài tập cơ bản sẽ tạo nền tảng vững chắc cho việc học các phép tính phức tạp hơn.

Bài tập nâng cao và ứng dụng

Sau khi nắm vững kiến thức cơ bản, học sinh có thể tiến tới các bài tập nâng cao. Những bài toán này thường kết hợp nhiều phép tính khác nhau và đòi hỏi khả năng phân tích, suy luận.

Các bài toán ứng dụng thực tế như tính toán nhiệt độ, độ cao so với mực nước biển hay lãi suất ngân hàng đều liên quan đến phép tính với số âm và dương. Điều này cho thấy tầm quan trọng của việc nắm vững kiến thức này.

Phương pháp giải nhanh

Để giải nhanh các bài toán về số âm số dương, học sinh có thể áp dụng một số mẹo và kỹ thuật đặc biệt. Việc nhận biết nhanh dấu của kết quả dựa vào các số hạng ban đầu là một kỹ năng quan trọng.

Phương pháp ước lượng kết quả trước khi tính toán chi tiết cũng rất hữu ích. Điều này giúp tránh được những sai sót không đáng có và tiết kiệm thời gian làm bài.

Ngoài ra, việc ghi nhớ một số trường hợp đặc biệt và quy luật chung sẽ giúp việc tính toán trở nên nhanh chóng và chính xác hơn. Ví dụ như quy tắc nhân các số cùng dấu và trái dấu.

Khi xem xét vấn đề dương cộng âm ra gì, ta có thể thấy rằng sự tương tác giữa hai loại số này không chỉ đơn thuần là phép toán mà còn phản ánh nguyên lý cơ bản trong toán học. Qua các quy tắc cộng, trừ và ứng dụng trong thực tế, người học có thể dễ dàng nhìn nhận và vận dụng trong các tình huống khác nhau. Sự hiểu biết này sẽ giúp bạn tự tin hơn khi giải quyết các bài tập về số dương và âm trong quá trình học.