Tính góc giữa 2 đường thẳng trong không gian và mặt phẳng đơn giản

Góc giữa 2 đường thẳng là một khái niệm quan trọng trong hình học. Hiểu và tính chính xác góc giữa hai đường thẳng giúp học sinh phát triển kỹ năng tư duy logic. Bài viết này cung cấp công thức, phương pháp giải và ứng dụng thực tế. Hãy cùng khám phá các bước tính toán chi tiết và các ví dụ minh họa dễ hiểu.

Góc giữa 2 đường thẳng là gì và các trường hợp thường gặp trong hình học

Góc giữa 2 đường thẳng được định nghĩa là góc nhỏ nhất tạo bởi hai đường thẳng khi chúng cắt nhau tại một điểm. Đây là một khái niệm cơ bản và quan trọng trong hình học, liên quan mật thiết đến góc giữa 2 vecto trong không gian vector.

Khi hai đường thẳng cắt nhau, chúng tạo ra hai cặp góc đối đỉnh bằng nhau. Trong mỗi cặp góc kề bên nhau sẽ tạo thành hai góc phụ nhau, có tổng số đo là 180 độ. Điều này giúp ta dễ dàng xác định được góc giữa hai đường thẳng bất kỳ khi biết một trong các góc tạo thành.

Trong thực tế, góc giữa hai đường thẳng có thể thuộc một trong ba trường hợp chính. Trường hợp thứ nhất là góc vuông (90 độ), khi hai đường thẳng vuông góc với nhau. Trường hợp thứ hai là góc nhọn (nhỏ hơn 90 độ), và trường hợp thứ ba là góc tù (lớn hơn 90 độ). Ngoài ra còn có trường hợp đặc biệt khi hai đường thẳng song song, khi đó góc giữa chúng bằng 0 độ.

Công thức tính góc giữa hai đường thẳng trong mặt phẳng và không gian

Việc tính góc giữa 2 đường thẳng là một bài toán quan trọng trong hình học. Để xác định góc giữa hai đường thẳng, ta cần dựa vào phương trình của chúng và áp dụng các công thức phù hợp tùy thuộc vào không gian đang xét.

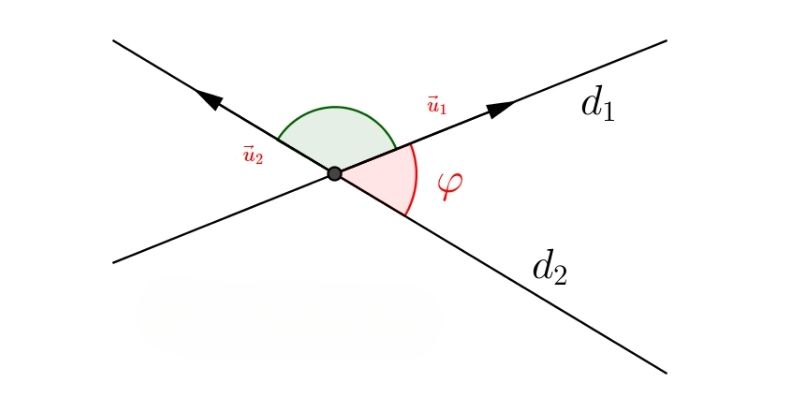
Khi tính góc giữa hai đường thẳng, ta thường phải xác định khoảng cách giữa 2 đường thẳng và công thức tính khoảng cách 2 điểm để có cái nhìn tổng quan về vị trí tương đối của chúng. Từ đó áp dụng các công thức tính góc giữa hai đường thẳng phù hợp.

Công thức tính góc giữa hai đường thẳng trong mặt phẳng Oxy

Trong mặt phẳng Oxy, góc giữa hai đường thẳng d1: y = a1x + b1 và d2: y = a2x + b2 được tính bằng công thức:
|tanφ| = |a1 – a2|/(1 + a1a2), với φ là góc giữa hai đường thẳng.

Nếu hai đường thẳng có dạng tổng quát A1x + B1y + C1 = 0 và A2x + B2y + C2 = 0, ta có công thức:
cosφ = |A1A2 + B1B2|/√[(A1² + B1²)(A2² + B2²)]

Công thức tính góc giữa hai đường thẳng trong không gian Oxyz

Khi xét trong không gian Oxyz, góc giữa hai đường thẳng trong không gian được tính dựa trên vector chỉ phương của chúng. Nếu d1 có vector chỉ phương v1(x1,y1,z1) và d2 có vector chỉ phương v2(x2,y2,z2), góc φ được tính theo công thức:
cosφ = |x1x2 + y1y2 + z1z2|/√[(x1² + y1² + z1²)(x2² + y2² + z2²)]

Vector chỉ phương có thể xác định từ phương trình tham số của đường thẳng hoặc từ hai điểm bất kỳ trên đường thẳng đó.

Các trường hợp đặc biệt khi tính góc giữa hai đường thẳng

Khi hai đường thẳng song song, góc giữa chúng bằng 0° hoặc 180°. Vector chỉ phương của chúng cùng phương hoặc ngược phương.

Khi hai đường thẳng vuông góc, góc giữa chúng bằng 90°. Tích vô hướng của vector chỉ phương bằng 0.

Trường hợp hai đường thẳng chéo nhau trong không gian, góc giữa chúng được xác định bằng góc giữa hai vector chỉ phương tương ứng.

Phương pháp xác định góc giữa hai đường thẳng chéo nhau trong không gian

Góc giữa hai đường thẳng chéo nhau trong không gian được xác định thông qua vector chỉ phương của hai đường thẳng đó. Phương pháp này dựa trên công thức tính góc giữa hai vector trong không gian và áp dụng các kiến thức về phép chiếu vuông góc.

Khi hai đường thẳng chéo nhau, chúng không cắt nhau và không song song với nhau. Để tìm góc giữa hai đường thẳng chéo nhau, ta cần xác định vector chỉ phương của mỗi đường thẳng, sau đó áp dụng công thức tính góc giữa hai vector. Phương pháp này liên quan mật thiết đến góc giữa 2 mặt phẳng và giao tuyến 2 mặt phẳng khi nghiên cứu hình học không gian.

Các bước xác định góc giữa hai đường thẳng chéo nhau

Bước 1: Xác định vector chỉ phương của hai đường thẳng thông qua phương trình tham số hoặc phương trình chính tắc.

Bước 2: Chuẩn hóa hai vector chỉ phương để có độ dài bằng 1, giúp tính toán chính xác hơn.

Bước 3: Áp dụng công thức tính góc giữa hai vector:
cos α = |a⃗.b⃗|/(|a⃗|.|b⃗|)
Trong đó: α là góc cần tìm, a⃗ và b⃗ là hai vector chỉ phương đã chuẩn hóa.

Ví dụ minh họa cách tìm góc giữa hai đường thẳng chéo nhau

Cho hai đường thẳng d1: (x-1)/2 = (y+1)/3 = (z-2)/1 và d2: x/1 = (y-2)/2 = (z+1)/(-1)

Vector chỉ phương của d1 là v⃗1(2,3,1) và d2 là v⃗2(1,2,-1)

Áp dụng công thức:
cos α = (2.1 + 3.2 + 1.(-1))/√[(22+32+12)(12+22+(-1)2)]
= 7/√(14.6) = 7/√84

Vậy góc giữa hai đường thẳng là α = arccos(7/√84) ≈ 40,3°

Kết quả trên minh họa cách áp dụng phương pháp tính góc một cách chính xác và hiệu quả.

Bài tập và phương pháp giải về góc giữa hai đường thẳng

Góc giữa 2 đường thẳng là một khái niệm quan trọng trong hình học, được ứng dụng rộng rãi trong các bài toán thực tế. Để giải các bài tập liên quan, cần nắm vững công thức tính góc và các phương pháp tiếp cận phù hợp với từng dạng bài.

Việc xác định góc giữa hai đường thẳng phụ thuộc vào vị trí tương đối của chúng. Điều kiện hai đường thẳng song song, trùng, cắt nhau là yếu tố quyết định phương pháp giải phù hợp. Cách tính góc giữa hai đường thẳng cần dựa trên vector chỉ phương hoặc hệ số góc tùy thuộc vào dạng bài.

Bài tập mẫu về tính góc giữa hai đường thẳng trong mặt phẳng

Khi giải bài tập về góc trong mặt phẳng, ta thường sử dụng công thức liên quan đến hệ số góc. Nếu d1, d2 là hai đường thẳng có hệ số góc k1, k2, góc giữa chúng được tính theo công thức: tanα = |(k1-k2)/(1+k1k2)|.

Trong trường hợp hai đường thẳng cắt nhau, việc tìm tọa độ giao điểm của 2 đường thẳng sẽ giúp xác định vị trí chính xác của góc cần tính. Góc giữa hai đường thẳng luôn được chọn là góc nhỏ nhất trong hai góc kề bù.

Bài tập mẫu về góc giữa hai đường thẳng trong không gian

Tính góc giữa hai đường thẳng trong không gian đòi hỏi sử dụng vector chỉ phương. Nếu a và b là hai vector chỉ phương của hai đường thẳng, góc giữa chúng được tính theo công thức: cosα = |a.b|/(|a|.|b|).

Phương pháp này áp dụng cho mọi trường hợp hai đường thẳng chéo nhau hoặc cắt nhau trong không gian. Việc xác định vector chỉ phương từ phương trình tham số của đường thẳng là bước quan trọng đầu tiên.

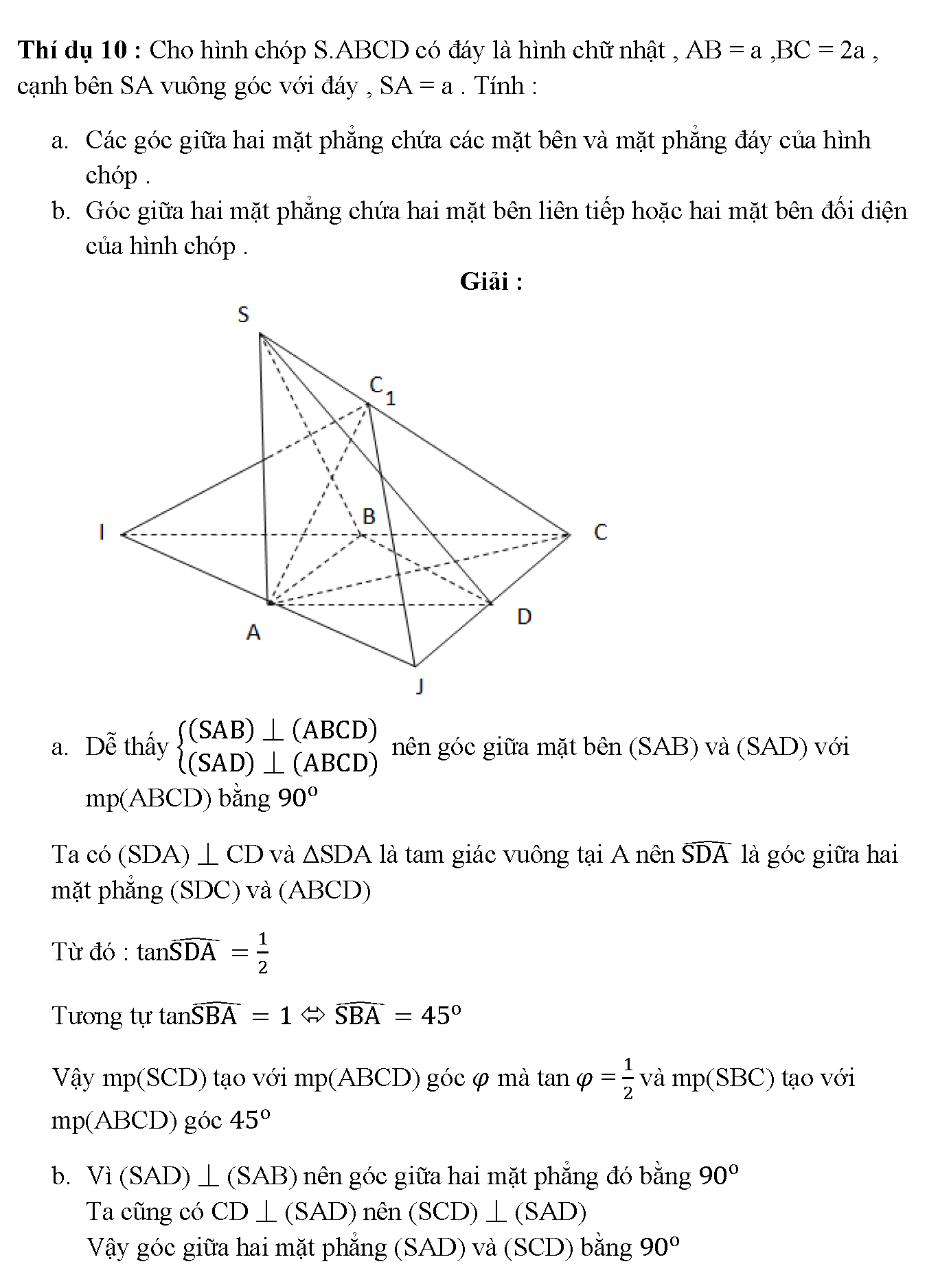
Các dạng bài tập thường gặp và phương pháp giải

Dạng 1: Tính góc giữa hai đường thẳng cho bởi phương trình tổng quát

• Chuyển về dạng phương trình y = kx + b
• Tính hệ số góc k1, k2
• Áp dụng công thức tính góc

Dạng 2: Tính góc giữa hai đường thẳng trong không gian

• Xác định vector chỉ phương từ phương trình
• Tính tích vô hướng và độ dài vector
• Áp dụng công thức cosα

Dạng 3: Tìm góc khi biết điều kiện hình học

• Vẽ hình minh họa
• Thiết lập hệ phương trình từ giả thiết
• Giải hệ và tính góc cần tìm

Các dạng bài tập này đều yêu cầu nắm vững kiến thức về vector, phép chiếu và các công thức lượng giác cơ bản.

Ứng dụng của góc giữa hai đường thẳng trong thực tế và các bài toán hình học

Góc giữa 2 đường thẳng có nhiều ứng dụng quan trọng trong đời sống và khoa học kỹ thuật. Việc xác định góc giữa các đường thẳng giúp tính toán chính xác trong thiết kế, xây dựng và giải quyết các bài toán hình học phức tạp.

Trong thực tế, góc giữa các đường thẳng được ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, xây dựng, thiết kế nội thất và quy hoạch đô thị. Đặc biệt, góc giữa hai đường thẳng bất kì trong không gian đóng vai trò then chốt trong việc tính toán kết cấu và thiết kế các công trình phức tạp.

Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc, góc giữa các đường thẳng được sử dụng để thiết kế mái nhà, cầu thang và các chi tiết trang trí. Theo kiến trúc sư Frank Gehry, việc tính toán chính xác góc nghiêng của các mặt phẳng và đường thẳng là yếu tố quyết định sự ổn định của công trình.

Các kỹ sư xây dựng thường áp dụng nguyên lý về góc giữa các đường thẳng để thiết kế hệ thống dầm, cột và các kết cấu chịu lực. Công ty ARUP đã sử dụng phương pháp này trong việc thiết kế Nhà hát Opera Sydney, tạo nên những đường cong độc đáo mà vẫn đảm bảo độ bền vững.

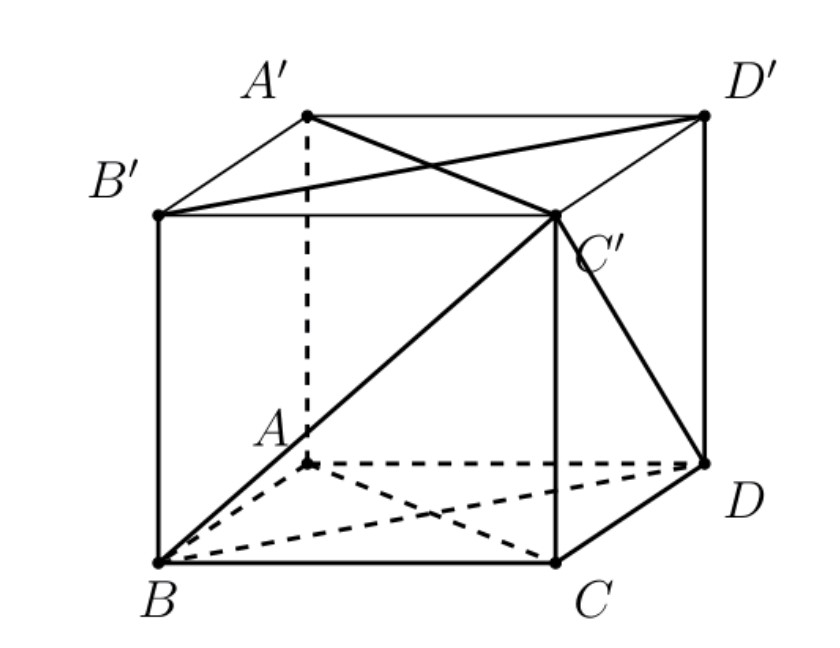
Ứng dụng trong các bài toán hình học không gian

Trong hình học không gian, góc giữa các đường thẳng là công cụ quan trọng để giải quyết nhiều bài toán phức tạp. Việc xác định góc giữa hai đường chéo của hình hộp chữ nhật giúp tính được thể tích và các yếu tố khác của khối đa diện.

Phương pháp tính góc giữa đường thẳng và mặt phẳng Phương pháp tính góc trong không gian được ứng dụng rộng rãi trong thiết kế máy bay và tàu vũ trụ. NASA đã sử dụng các tính toán này để xác định góc nghiêng tối ưu cho các tấm pin năng lượng mặt trời trên vệ tinh.

Trong công nghiệp sản xuất, việc tính toán góc giữa các đường thẳng giúp thiết kế chính xác các chi tiết máy, đảm bảo sự khớp nối hoàn hảo giữa các bộ phận. Điều này đặc biệt quan trọng trong sản xuất ô tô và máy móc công nghiệp.

Trong xã hội ngày nay, góc giữa 2 đường thẳng đóng vai trò quan trọng trong nhiều lĩnh vực, từ kiến trúc đến toán học. Bài viết đã cung cấp những công thức tính góc trong mặt phẳng và không gian, đồng thời hướng dẫn các phương pháp xác định góc hiệu quả. Nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán phức tạp hơn liên quan đến hình học một cách dễ dàng.