Hệ thức lượng trong tam giác vuông – công thức, kỹ năng và bài tập ứng dụng hiệu quả

Hệ thức lượng trong tam giác vuông đóng vai trò quan trọng trong việc giải quyết các bài toán hình học. Bằng các công thức cụ thể, bạn sẽ được hướng dẫn cách áp dụng chúng để tính toán các cạnh và góc. Bài viết sẽ giúp bạn nắm vững quy tắc, kỹ năng cần thiết để giải bài tập một cách chính xác.

Hệ thức lượng trong tam giác vuông là các công thức biểu diễn mối quan hệ giữa các cạnh và góc trong tam giác vuông

Hệ thức lượng trong tam giác vuông là những công thức toán học thể hiện mối liên hệ giữa các yếu tố trong tam giác vuông như cạnh góc vuông, cạnh huyền và các góc nhọn. Các công thức này giúp tính toán chính xác các yếu tố chưa biết khi đã có một số yếu tố cho trước.

Trong toán học, hệ thức lượng đóng vai trò quan trọng để giải quyết các bài toán thực tế liên quan đến tam giác vuông. Ví dụ như tính chiều cao tòa nhà, độ nghiêng của mái nhà hay khoảng cách giữa hai điểm không thể đo trực tiếp. Các công thức này được phát triển từ định lý Pythagore và các tỷ số lượng giác cơ bản.

Khi được hỏi “hệ thức là gì“, có thể hiểu đây là những công thức toán học biểu diễn mối quan hệ giữa các đại lượng trong một hình học cụ thể. Trong tam giác vuông, các hệ thức quan trọng bao gồm định lý Pythagore, các hệ thức về tỷ số lượng giác và các hệ thức về đường cao, đường trung tuyến.

Các hệ thức lượng cơ bản trong tam giác vuông và cách áp dụng vào bài toán

Hệ thức lượng trong tam giác vuông là những công thức quan trọng giúp giải quyết nhiều bài toán hình học. Các công thức này được xây dựng dựa trên mối quan hệ giữa các cạnh và góc trong tam giác vuông. công thức viet cung cấp chi tiết về cách áp dụng các hệ thức vào từng dạng bài toán cụ thể.

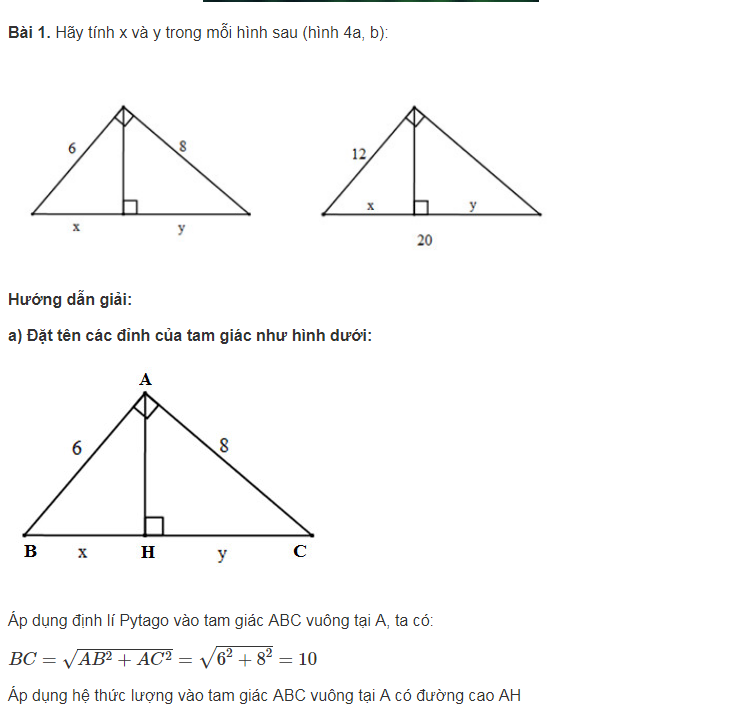
Các hệ thức lượng trong tam giác vuông được chia thành 3 nhóm chính, mỗi nhóm có những đặc điểm và ứng dụng riêng. Việc nắm vững các nhóm hệ thức này giúp giải quyết hiệu quả các bài toán về tam giác vuông.

Hệ thức về tỷ số giữa cạnh góc vuông và cạnh huyền

Trong tam giác vuông, tỷ số giữa cạnh góc vuông và cạnh huyền luôn bằng hàm sin hoặc cos của góc nhọn. Cụ thể, cạnh đối chia huyền bằng sin của góc nhọn kề, cạnh kề chia huyền bằng cos của góc nhọn kề.

Các tỷ số này có ý nghĩa quan trọng khi cần tìm độ dài cạnh hoặc số đo góc trong tam giác vuông. Đặc biệt trong các bài toán thực tế như đo chiều cao công trình, khoảng cách giữa hai điểm.

Hệ thức về tỷ số giữa hai cạnh góc vuông

Hệ thức lượng giác về tỷ số giữa hai cạnh góc vuông được thể hiện thông qua hàm tang. Tỷ số giữa cạnh đối và cạnh kề của một góc nhọn bằng tang của góc đó.

Hệ thức này thường được áp dụng khi cần tìm độ dài một cạnh góc vuông khi biết cạnh góc vuông còn lại và một góc nhọn. Ví dụ trong ngành xây dựng, khi tính độ dốc của mái nhà, người ta thường sử dụng tỷ số này.

Hệ thức về bình phương các cạnh

Định lý Pytago là hệ thức quan trọng nhất về bình phương các cạnh trong tam giác vuông. Theo đó, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Ngoài ra còn có các hệ thức mở rộng như: bình phương cạnh đối của một góc nhọn bằng tích của huyền với hình chiếu cạnh đó trên huyền. Các hệ thức này có ứng dụng rộng rãi trong việc tính toán khoảng cách, diện tích và thể tích các hình học phức tạp.

Việc kết hợp linh hoạt các hệ thức trên giúp giải quyết hiệu quả nhiều dạng bài toán về tam giác vuông trong thực tế.

Phương pháp chứng minh và giải toán sử dụng hệ thức lượng trong tam giác vuông lớp 9

Việc nắm vững hệ thức lượng trong tam giác vuông lớp 9 là nền tảng quan trọng để giải các bài toán hình học. Các công thức cơ bản như công thức nhân liên hợp thường được áp dụng kết hợp với các hệ thức lượng để chứng minh và giải toán hiệu quả.

Khi áp dụng hệ thức lượng trong tam giác lớp 9, việc xác định đúng các yếu tố và mối quan hệ giữa chúng là bước đầu tiên. Các phép biến đổi như đạo hàm sin cũng thường được sử dụng để chứng minh các hệ thức lượng tam giác phức tạp.

Các dạng bài tập thường gặp

Dạng bài tập chứng minh đẳng thức là phổ biến nhất, đòi hỏi vận dụng linh hoạt các hệ thức về đường cao, đường trung tuyến và đường phân giác. Việc chứng minh thường bắt đầu từ việc vẽ hình và xác định các yếu tố đã biết.

Dạng bài tập tính toán các yếu tố trong tam giác cũng xuất hiện thường xuyên. Các bài toán này thường yêu cầu tìm độ dài cạnh, số đo góc hoặc diện tích tam giác dựa trên các dữ kiện cho trước.

Phương pháp giải và chứng minh

Bước đầu tiên là vẽ hình chính xác và đầy đủ các yếu tố. Việc ghi nhận đầy đủ giả thiết và kết luận cần chứng minh giúp định hướng cách giải rõ ràng hơn.

Tiếp theo là xác định các mối liên hệ giữa các yếu tố trong tam giác, từ đó lựa chọn hệ thức phù hợp để áp dụng. Trong nhiều trường hợp, cần kết hợp nhiều hệ thức khác nhau để đi đến kết quả.

Cuối cùng là thực hiện các phép biến đổi đại số một cách chặt chẽ và logic để hoàn thành chứng minh hoặc tìm ra kết quả cần tính.

Bài tập mẫu và lời giải chi tiết

Bài toán về chứng minh đẳng thức trong tam giác vuông thường đòi hỏi sự kết hợp giữa kiến thức hình học và đại số. Ví dụ, để chứng minh một đẳng thức liên quan đến đường cao và cạnh huyền, ta thường sử dụng các tam giác đồng dạng được tạo bởi đường cao.

Với bài toán tính toán, việc áp dụng định lý Pytago kết hợp với các hệ thức về đường cao, đường trung tuyến sẽ giúp tìm ra lời giải. Quan trọng là phải kiểm tra kỹ kết quả và đơn vị đo để đảm bảo tính chính xác của bài giải.

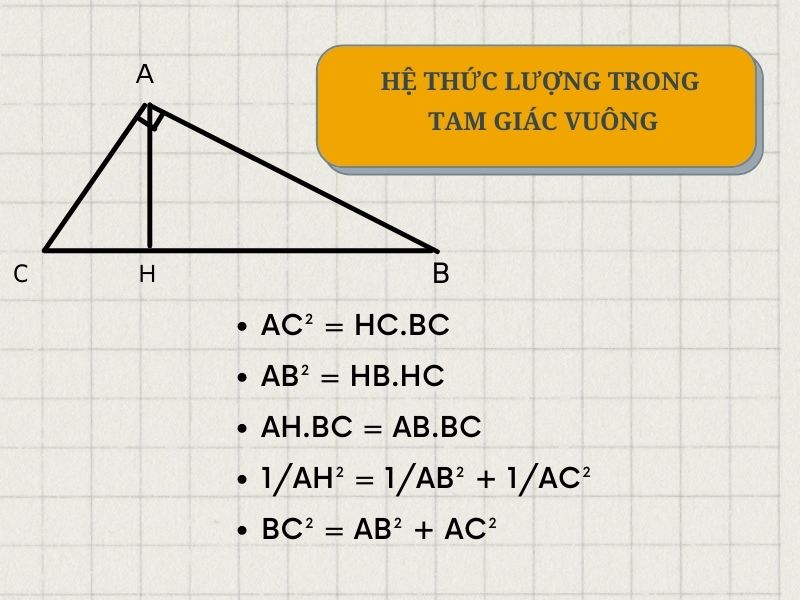
Các bài toán phức tạp thường yêu cầu phân tích kỹ hình vẽ để phát hiện các yếu tố trung gian, từ đó xây dựng các bước giải phù hợp dẫn đến kết quả cuối cùng.

Mối liên hệ giữa hệ thức lượng và các kiến thức hình học khác

Hệ thức lượng trong tam giác vuông có mối liên hệ chặt chẽ với nhiều kiến thức hình học quan trọng khác. Các công thức lượng giác trong tam giác giúp giải quyết nhiều bài toán phức tạp về đo lường và tính toán trong không gian. Đặc biệt, hệ thức lượng giác trong tam giác vuông còn là nền tảng để phát triển các công thức nâng cao trong hình học phẳng và không gian.

Ứng dụng trong tam giác đồng dạng

Khi áp dụng trường hợp đồng dạng của tam giác vuông, các hệ thức lượng giúp thiết lập mối quan hệ tỷ lệ giữa các cạnh tương ứng. Điều này tạo nên công cụ mạnh mẽ để giải các bài toán về độ dài, diện tích và tỷ số.

Việc kết hợp giữa tính chất đồng dạng và các hệ thức lượng còn mở rộng khả năng giải quyết các bài toán về góc và đường cao trong tam giác. Các phép biến đổi đồng dạng kết hợp với Lượng giác tạo nên phương pháp hiệu quả để tính toán các yếu tố chưa biết trong hình học.

Liên hệ với định lý Pytago

Định lý Pytago và các hệ thức lượng có mối liên hệ mật thiết thông qua các tỷ số lượng giác. Khi xét một tam giác vuông với các cạnh góc vuông a, b và cạnh huyền c, ta có thể biểu diễn sin và cos thông qua tỷ số các cạnh.

Mối quan hệ này không chỉ giúp chứng minh các bài toán về tam giác vuông mà còn mở rộng sang các ứng dụng trong thực tế như đo đạc địa hình, xây dựng và thiết kế công trình. Việc kết hợp định lý Pytago với các hệ thức lượng tạo nên công cụ toán học mạnh mẽ trong nhiều lĩnh vực.

Mở rộng cho các bài toán phức tạp

Các hệ thức lượng không chỉ giới hạn trong tam giác vuông mà còn được mở rộng cho các bài toán phức tạp hơn. Trong các bài toán về đa giác và hình học không gian, việc phân tích thành các tam giác vuông kết hợp với hệ thức lượng tạo nên phương pháp giải hiệu quả.

Ứng dụng này đặc biệt quan trọng trong các bài toán tối ưu hóa, thiết kế kỹ thuật và mô phỏng 3D. Các công ty công nghệ lớn như Autodesk đã ứng dụng các nguyên lý này trong phần mềm thiết kế CAD của họ, giúp tính toán chính xác các thông số kỹ thuật trong không gian ba chiều.

Các công cụ và phần mềm hỗ trợ tính toán hệ thức lượng trong tam giác vuông

Việc tính toán hệ thức lượng trong tam giác vuông có thể trở nên dễ dàng và chính xác hơn nhờ các công cụ hỗ trợ. Các phương tiện này giúp người học kiểm chứng kết quả và trực quan hóa các công thức hệ thức lượng một cách hiệu quả.

Máy tính khoa học và các phím chức năng

Máy tính khoa học là công cụ cơ bản và thiết yếu để tính toán các giá trị trong tam giác vuông. Các phím sin, cos, tan giúp tính nhanh tỷ số lượng giác, trong khi phím sqrt hỗ trợ tính căn bậc hai cho định lý Pytago.

Việc sử dụng phím M+ và M- còn cho phép lưu trữ các kết quả trung gian, giúp quá trình tính toán được liên tục và tránh sai sót. Đặc biệt, chế độ DEG/RAD cho phép chuyển đổi linh hoạt giữa đơn vị độ và radian khi cần thiết.

Phần mềm hình học động GeoGebra

GeoGebra mang đến khả năng trực quan hóa các he thuc luong thông qua mô phỏng động. Phần mềm cho phép vẽ tam giác vuông với các kích thước tùy chỉnh, đồng thời hiển thị các giá trị cạnh và góc theo thời gian thực.

Người dùng có thể kéo thả các đỉnh để thay đổi hình dạng tam giác, quan sát sự thay đổi của các hệ thức. Tính năng đo lường tự động giúp kiểm chứng các công thức một cách nhanh chóng và chính xác.

Khả năng xuất hình ảnh và animation của GeoGebra còn hỗ trợ việc tạo tài liệu học tập sinh động. Điều này đặc biệt hữu ích cho giáo viên và học sinh trong quá trình giảng dạy và học tập.

Các website tính toán online

Các trang web chuyên về toán học cung cấp nhiều công cụ tính toán trực tuyến miễn phí. Các calculator này không chỉ cho kết quả mà còn hiển thị chi tiết các bước giải, giúp người học hiểu rõ quy trình áp dụng công thức.

Một số website còn tích hợp tính năng vẽ hình minh họa, cho phép nhập các giá trị đã biết và tự động tính toán các yếu tố còn lại. Tính năng lưu trữ và chia sẻ kết quả tạo điều kiện thuận lợi cho việc học nhóm và trao đổi bài tập.

Tuy nhiên, cần lưu ý rằng các công cụ online đôi khi đòi hỏi kết nối internet ổn định và có thể chứa quảng cáo gây phiền nhiễu. Vì vậy, nên kết hợp sử dụng với các phương tiện offline để đảm bảo hiệu quả học tập tốt nhất.

Hệ thức lượng trong tam giác vuông là một công cụ quan trọng giúp chúng ta hiểu rõ mối liên hệ giữa các cạnh và góc trong tam giác. Nắm vững các công thức này còn giúp giải quyết nhiều bài toán hình học phức tạp hơn. Từ những hệ thức cơ bản cho đến những ứng dụng thú vị trong các định lý, việc sử dụng hệ thức lượng đem lại hiệu quả cao trong học tập và giải toán.