Hình cầu là gì? Tính chất, công thức liên quan hình cầu

Hình cầu là phần kiến thức quan trọng trong chương trình toán THPT. Hình cầu là gì, các tính chất đặc trưng, công thức và ứng dụng giải một số bài toán liên quan đến hình cầu là những vấn đề được nhiều học sinh quan tâm. Hãy theo dõi bài viết sau đây để tìm hiểu xem khối cầu là gì cùng các tính chất, công thức và bài tập vận dụng nhé.

Hình cầu là gì? Khái niệm đơn giản

Hình cầu là một mặt cong hoàn hảo trong không gian ba chiều, được tạo thành từ tất cả các điểm cách đều một điểm cố định (hay còn gọi là tâm hình cầu, thường ký hiệu là O). Khoảng cách từ tâm đến bất kỳ điểm nào trên bề mặt hình cầu được gọi là bán kính, thường ký hiệu là R.

>>> Xem thêm: Khối cầu là gì? Định nghĩa, đặc điểm và ứng dụng thực tế

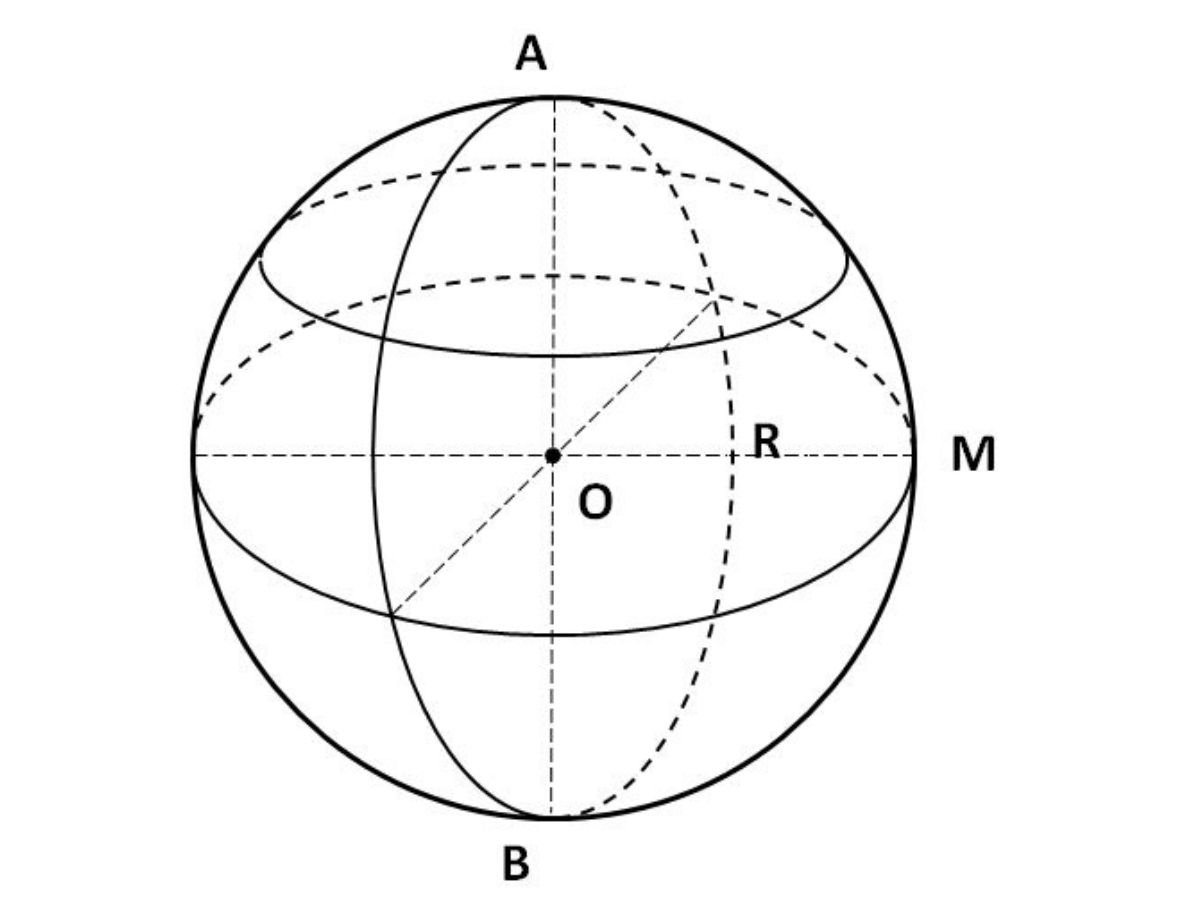
Hình cầu được tạo ra khi xoay nửa hình tròn một vòng quanh đường kính của hình tròn đó. Ví dụ, khi xoay nửa hình tròn tâm O, bán kính R một vòng quanh trục (đường kính) AB cố định trong không gian ba chiều, ta sẽ tạo thành một hình cầu tâm O.

Tính chất của hình cầu

Dưới đây là một số tính chất đặc trưng của hình cầu trong toán học:

Tính chất đối xứng: Hình cầu có vô số trục đối xứng là bất kỳ đường thẳng nào đi qua tâm của hình cầu. Hình cầu có vô số mặt phẳng đối xứng là bất kỳ mặt phẳng nào đi qua tâm và cắt hình cầu thành hai phần bằng nhau.
Tính chất liên quan đến cắt, tiếp xúc: Khi cắt hình cầu bởi một mặt phẳng, ta được một hình tròn có bán kính R nếu mặt phẳng đi qua tâm hình cầu, hoặc một hình tròn có bán kính bé hơn R nếu mặt phẳng đó không đi qua tâm hình cầu. Hai hình cầu có thể tiếp xúc ngoài, tiếp xúc trong hoặc cắt nhau.

Các công thức nhất định phải ghi nhớ

Học sinh cần hiểu và nắm rõ các công thức quan trọng sau đây:

Công thức tính chu vi hình cầu

Như đã đề cập ở trên, chu vi khối cầu thực chất là chu vi của đường tròn lớn nhất trên hình cầu. Vì vậy, chu vi của hình cầu công thức cũng tương tự như công thức tính chu vi của một đường tròn:

C = 2. π . r

trong đó:

C là chu vi của đường tròn lớn trên hình cầu.
R là bán kính của hình cầu.
π là hằng số toán học xấp xỉ 3.14.

Với công thức này, chúng ta có thể dễ dàng tính toán chu vi của hình cầu nếu biết bán kính của nó.

Diện tích mặt cầu

Vậy diện tích hình cầu là gì? Để tính diện tích mặt cầu có bán kính R, học sinh áp dụng công thức sau:

S=4.π

Trong đó:

S: Diện tích mặt cầu (đơn vị m², cm²,…)
π: Số pi, xấp xỉ bằng 3.14159
r: Bán kính mặt cầu (đơn vị m, cm, …)

Thể tích hình cầu

Thể tích hình cầu có bán kính R được tính bằng công thức:

$$\mathrm V=\frac43.\mathrm\pi.\mathrm r^3$$

Trong đó:

V: Thể tích hình cầu (đơn vị m³, cm³,…)
π: Số pi, xấp xỉ bằng 3.14159
r: Bán kính hình cầu (đơn vị mét, cm,…)

Đường kính hình cầu

Đường kính D của hình cầu có bán kính R được tính bằng công thức:

$$D=2.r$$

Trong đó:

D: Đường kính hình cầu (đơn vị m, cm,…)
r: Bán kính hình cầu (đơn vị m, cm,…)

>>> Xem thêm: Chu vi hình cầu: Hướng dẫn công thức tính và cách giải nhanh

Công thức tính thể tích hình chỏm cầu

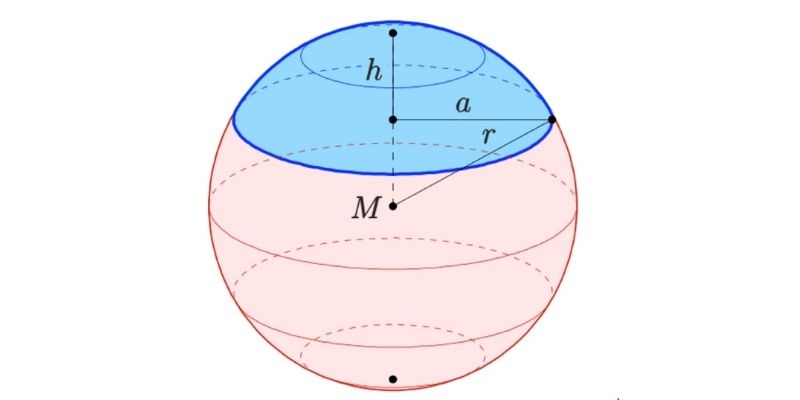
Hình chỏm cầu là một phần không gian được tạo ra bởi một mặt phẳng cắt qua hình cầu. Hình chỏm cầu cũng có đỉnh, đáy và các mặt bên với các đặc điểm sau:

Đỉnh của chỏm cầu: Điểm cao nhất trên bề mặt chỏm cầu, điểm xa nhất so với mặt phẳng cắt.

Đáy của chỏm cầu: Vùng bề mặt trên hình cầu được giới hạn bởi mặt phẳng cắt.

Chiều cao của chỏm cầu: Khoảng cách từ đỉnh đến mặt phẳng cắt, được đo dọc theo đường vuông góc với mặt phẳng cắt.

Hình chỏm cầu được ứng dụng đa dạng trong các ngành kỹ thuật, kiến trúc, vật lý,…Thể tích của hình chỏm cầu được tính bằng công thức sau:

$$V=\frac13.\mathrm\pi.\mathrm h^2.(3.\mathrm R-\mathrm h)$$

Trong đó:

V: Thể tích hình chỏm cầu (đơn vị m³, cm³,…)
π: Số pi, xấp xỉ bằng 3.14159
h: Chiều cao của hình chỏm cầu từ mặt phẳng đáy đến đỉnh của chỏm cầu (đơn vị m, cm,…)
R: Bán kính của hình cầu gốc (đơn vị m, cm,…)

Ví dụ bài tập về hình cầu

Bài tập 1:

Một hình cầu có bán kính 6 cm. Tính diện tích mặt cầu và thể tích hình cầu đó.

Bài giải:

Diện tích mặt cầu là:

$$\mathrm S=4.\mathrm\pi.\mathrm r^2=4.\mathrm\pi.6^2=144.\mathrm\pi\;(\mathrm{cm}^2)$$

Thể tích hình cầu là:

$$\mathrm V=\frac43.\mathrm\pi.\mathrm r^3=\frac43.\mathrm\pi.6^3=288.\mathrm\pi\;(\mathrm{cm}^3)$$

Bài tập 2:

Một khối cầu gỗ có bán kính 4 cm. Người ta sơn toàn bộ mặt ngoài của khối cầu. Tính diện tích cần sơn.

Bài giải:

Diện tích cần sơn bằng diện tích mặt cầu là:

$$S=4.\mathrm\pi.\mathrm r^2=4.\mathrm\pi.4^2=64.\mathrm\pi\;(\mathrm{cm}^2)$$

Bài tập 3: Cho một hình cầu có thể tích V = 288π cm³. Hãy tính đường kính của hình cầu.

Giải:

Từ công thức tính thể tích hình cầu, ta có:

$$\mathrm V=\frac43.\mathrm\pi.\mathrm r^3$$

Với V = 288π cm³, ta được: $$288=\frac43.\mathrm\pi.\mathrm r^3$$

Chia hai vế cho (4/3)π, ta có: r³ = 216 ⇔ r = 6 cm

Đường kính của hình cầu là d = 2r. Với r = 6cm, ta có: d = 2.6 = 12 cm

Vậy đường kính của hình cầu là 12 cm.

Bài tập 4: Cho một hình chỏm cầu có chiều cao h = 5 cm và bán kính hình cầu R = 8 cm. Tính thể tích của hình chỏm cầu.

Giải:

Thay h = 5 cm và R = 8 cm vào công thức $$V=\frac13.\mathrm\pi.\mathrm h^2.(3.\mathrm R-\mathrm h)$$

Ta được:

$$V=\frac13.\mathrm\pi.\mathrm 5^2.(3.\mathrm 8-\mathrm 5)$$

V ≈ 166.22 cm³

Vậy thể tích của hình chỏm cầu xấp xỉ bằng 166.22 cm³.

Bài viết đã trả lời câu hỏi hình cầu là gì, các tính chất riêng biệt, công thức tính và một số bài tập ứng dụng tiêu biểu. Hy vọng với những kiến thức trên, các bạn học sinh có thể hiểu rõ hơn về loại hình học không gian này.