Kiểm định giả thuyết thống kê là một công cụ quan trọng trong phân tích dữ liệu, giúp ta đưa ra kết luận về một tập dữ liệu dựa trên bằng chứng thu thập được. Nó được sử dụng rộng rãi trong nhiều lĩnh vực như khoa học, kinh tế, y học, tâm lý học…
Khái niệm kiểm định giả thuyết thống kê
Kiểm định giả thuyết thống kê là một quy trình logic nhằm xác định xem một tuyên bố cụ thể về một tập dữ liệu (gọi là giả thuyết) có độ tin cậy, và có ý nghĩa thống kê hay không. Quá trình kiểm định này bao gồm các bước như sau:
- Bước 1. Đặt ra giả thuyết: Cách đặt giả thuyết trong kiểm định như sau:
- Giả thuyết H0 (giả thuyết không): là tuyên bố mặc định, thường là tuyên bố “không có sự khác biệt” hoặc “không có mối liên hệ” giữa các biến.
- Giả thuyết H1 (giả thuyết đối lập): là tuyên bố thay thế cho H0, thể hiện điều mà bạn muốn chứng minh.
- Bước 2. Thu thập dữ liệu: Thu thập một mẫu ngẫu nhiên từ tập dữ liệu và ghi chép các giá trị của các biến liên quan.
- Bước 3. Chọn thống kê kiểm định: Lựa chọn một thống kê phù hợp để đánh giá mức độ phù hợp của dữ liệu với giả thuyết H0.
- Bước 4. Xác định mức độ ý nghĩa: Chọn mức độ ý nghĩa (α), thường là 0.05 hoặc 0.01, để xác định mức độ tin cậy của kết quả kiểm định.
- Bước 5. Tính toán giá trị p: Sử dụng thống kê kiểm định và dữ liệu thu thập được để tính toán giá trị p.
- Bước 6. Ra quyết định: So sánh giá trị p với mức độ ý nghĩa:
- Nếu p < α: Từ chối H0, chấp nhận H1 (có ý nghĩa thống kê).
- Nếu p ≥ α: Không đủ bằng chứng để từ chối H0, giữ nguyên H0 (không có ý nghĩa thống kê).

Các loại kiểm định phổ biến
Có nhiều loại kiểm định giả thuyết khác nhau, được phân loại theo các tiêu chí như loại dữ liệu, số lượng mẫu và số lượng biến. Một số loại kiểm định phổ biến có thể kể đến như:
- Kiểm định t: Kiểm định trung bình mẫu khác nhau, so sánh trung bình của hai mẫu độc lập hoặc hai mẫu phụ thuộc.
- Kiểm định ANOVA: Kiểm định sự khác biệt giữa ba hoặc nhiều trung bình mẫu.
- Kiểm định chi-square: Kiểm định tần suất, so sánh tỷ lệ xuất hiện của các biến phân loại.
- Kiểm định hồi quy: Đánh giá mối liên hệ tuyến tính giữa các biến.
- Kiểm định phi tham số: Sử dụng cho dữ liệu không tuân theo phân phối chuẩn.
Lý thuyết thống kê nền tảng
Trước khi đi sâu vào tính giá trị kiểm định, bạn cần nắm vững một số khái niệm thống kê cơ bản như:
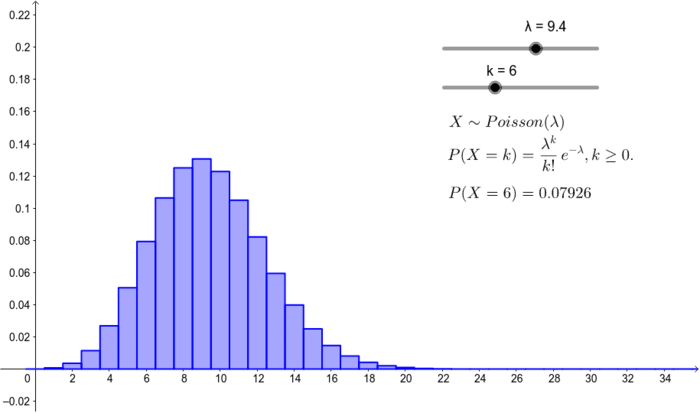
- Phân phối xác suất: Mô tả khả năng xảy ra của các giá trị khác nhau trong một tập dữ liệu.
- Mức độ ý nghĩa (α): Xác suất mắc sai lầm loại 1 (từ chối giả thuyết đúng).
- Giá trị p: Xác suất quan sát được thống kê kiểm định cực đoan hoặc hơn nếu giả thuyết đúng.
- Độ tin cậy (1 – α): Xác suất đưa ra kết luận chính xác.
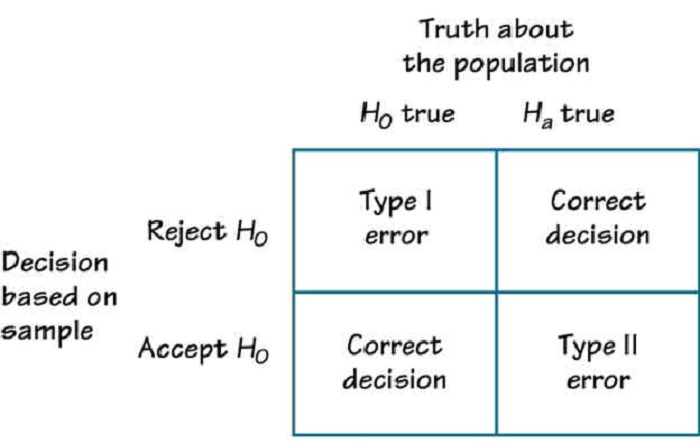
- Sai lầm loại 1: Từ chối giả thuyết đúng.
- Sai lầm loại 2: Chấp nhận giả thuyết sai.
Giả định thống kê
Hầu hết các phương pháp kiểm định giả thuyết đều dựa trên một số giả định thống kê nhất định. Việc vi phạm giả định có thể dẫn đến kết quả không chính xác. Một số giả định phổ biến bao gồm:
- Dữ liệu độc lập: Các quan sát trong tập dữ liệu không phụ thuộc lẫn nhau.
- Phân phối chuẩn: Dữ liệu tuân theo phân phối chuẩn (hình chuông).
- Đồng phương sai: Phương sai của các mẫu là bằng nhau.
Trước khi thực hiện kiểm định giả thuyết, cần kiểm tra tính hợp lệ của các giả định bằng các phương pháp thống kê thích hợp.
Kích thước mẫu
Kích thước mẫu ảnh hưởng trực tiếp đến độ tin cậy của kết quả kiểm định. Mẫu càng lớn, độ tin cậy càng cao. Tuy nhiên, việc thu thập dữ liệu mẫu lớn có thể tốn kém và mất thời gian. Do đó, cần lựa chọn kích thước mẫu phù hợp dựa trên mục tiêu nghiên cứu và ngân sách.
Hiệu ứng thống kê
Hiệu ứng thống kê là mức độ chênh lệch giữa hai nhóm hoặc giữa kết quả thực tế và kết quả mong đợi. Một hiệu ứng thống kê có ý nghĩa thực tế là hiệu ứng đủ lớn để có thể quan sát được trong thực tế và có thể tác động đến quyết định của bạn.
Có hai cách để đánh giá ý nghĩa thực tế của hiệu ứng thống kê:
- Kích thước hiệu ứng: Đây là thước đo độ lớn của hiệu ứng, thường được biểu thị bằng tỷ lệ hoặc tỷ lệ odds.
- Kiểm định ý nghĩa: Sử dụng các phương pháp thống kê để xác định xem hiệu ứng có đủ lớn để được coi là có ý nghĩa thực tế hay không.
Sai lầm loại 1 và loại 2
Sai lầm loại 1 xảy ra khi ta từ chối giả thuyết đúng, trong khi sai lầm loại 2 xảy ra khi ta chấp nhận giả thuyết sai. Cả hai sai lầm đều có thể dẫn đến hậu quả nghiêm trọng, tùy thuộc vào bối cảnh nghiên cứu.
Có thể giảm thiểu sai lầm loại 1 bằng cách tăng mức độ ý nghĩa (α) và giảm thiểu sai lầm loại 2 bằng cách tăng kích thước mẫu.
Cánh tính p value trong kiểm định
P-value là một số đo quan trọng trong kiểm định giả thuyết thống kê, thể hiện mức độ tin cậy của kết quả kiểm định. Giá trị p-value nhỏ cho thấy bằng chứng mạnh mẽ hơn chống lại giả thuyết không (H0), từ đó ủng hộ giả thuyết đối lập (H1). Có hai cách tính p value phổ biến trong kiểm định đó là: tính thủ công và tính bằng Excel.
Cách tính p-value thủ công
Việc tính toán thủ công p-value có thể phức tạp hơn, tùy thuộc vào phương pháp kiểm định được sử dụng. Cách tính p value bằng tay đối với một vài loại kiểm định phổ biến như sau:
- Kiểm định t:
- Giá trị thống kê kiểm định: t = (X̄1 – X̄2) / (SEp)
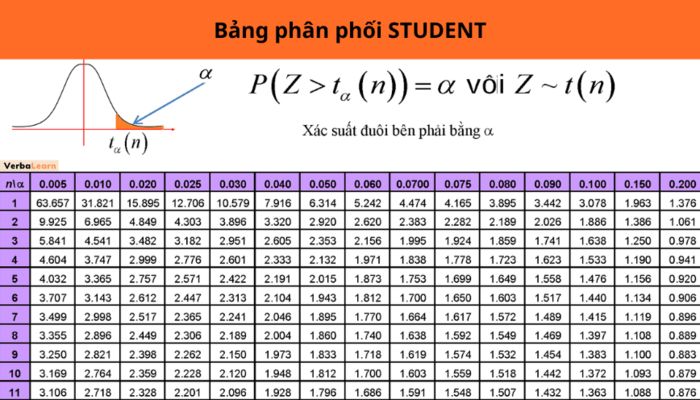
- Giá trị p: Sử dụng bảng phân phối t với n-2 bậc tự do (n là số lượng quan sát trong mỗi mẫu) và mức độ ý nghĩa α.
- Kiểm định ANOVA:
- Giá trị thống kê kiểm định: F = MSB / MSW
- Giá trị p: Sử dụng bảng phân phối F với k-1 và n-k bậc tự do (k là số lượng nhóm, n là tổng số lượng quan sát) và mức độ ý nghĩa α.
- Kiểm định chi-square:
- Giá trị thống kê kiểm định: χ² = Σ [(O – E)² / E]
- Giá trị p: Sử dụng bảng phân phối chi-square với k-1 bậc tự do (k là số lượng nhóm) và mức độ ý nghĩa α.
Cách tính p-value bằng Excel
Excel là một công cụ giúp tính toán p-value trong các bài toán kiểm định một cách dễ dàng và nhanh chóng bằng các hàm thống kê. Dưới đây là một số hàm phổ biến để tính p-value trong kiểm định:
- Hàm T.DIST: Tính toán p-value cho kiểm định t hai đuôi.
- Hàm TDIST: Tính toán p-value cho kiểm định t một đuôi.
- Hàm CHISQ.DIST.RT: Tính toán p-value cho kiểm định chi-square.
- Hàm NORMSDIST: Tính toán p-value cho kiểm định Z.
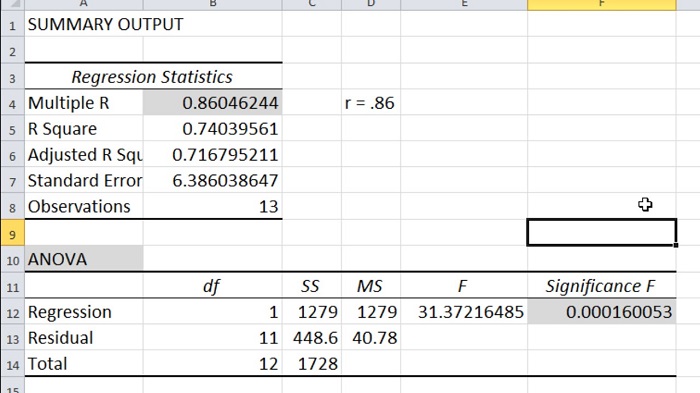
Cách tính p value trong Excel được thực hiện theo các bước như sau:
Bước 1: Mở phần mềm Excel và nhập dữ liệu vào các ô tính.
Bước 2: Sử dụng các hàm thống kê phù hợp để tính toán thống kê kiểm định (ví dụ: thống kê t, thống kê chi-square, thống kê Z).
Bước 3: Sử dụng hàm p-value tương ứng để tính toán giá trị p. Ví dụ:
- Kiểm định t hai đuôi: =T.DIST(thống_kê_t, số_bậc_tự_do)
- Kiểm định t một đuôi: =TDIST(thống_kê_t, số_bậc_tự_do, 1)
- Kiểm định chi-square: =CHISQ.DIST.RT(thống_kê_chi_square, số_bậc_tự_do)
- Kiểm định Z: =NORMSDIST(thống_kê_Z)
Bước 4: Giá trị p sẽ được hiển thị trong ô tính.
Lời kết
Kiểm định giả thuyết thống kê là một công cụ vô cùng hữu ích giúp ta đưa ra những kết luận có ý nghĩa dựa trên những dữ liệu thống kê sẵn có. Việc nắm vững các khái niệm, quy trình thực hiện và ứng dụng của kiểm định giả thuyết giúp bạn có thể học tập tốt hơn và đạt được điểm số cao trong môn học như Xác suất – Thống kê.
Nội dung bài viết