Nhân 2 ma trận là một phép toán cơ bản trong đại số tuyến tính, nó giúp cho việc giải các dạng bài tập ma trận trở nên nhanh chóng và dễ dàng hơn. Phép nhân ma trận đóng vai trò quan trọng trong nhiều lĩnh vực như toán cao cấp đại số, hình học giải tích, khoa học máy tính, vật lý, kinh tế,… Bài viết dưới đây của Hocthenao.vn sẽ hướng dẫn bạn chi tiết các bước nhân ma trận, điều kiện, tính chất và cách nhân ma trận trên máy tính Casio.
Định nghĩa nhân ma trận trong giải tích
Nhân 2 ma trận là phép toán kết hợp hai ma trận A và B để tạo ra một ma trận mới gọi là tích của A và B, ký hiệu là AB. Kết quả của phép nhân này sẽ là một ma trận mới có kích thước m x p (trong đó m là số hàng, p là sốt cột của ma trận).
Điều kiện để thực hiện nhân ma trận
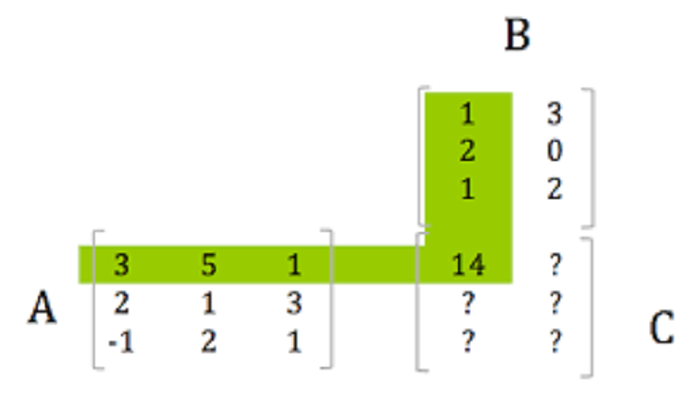
Để thực hiện phép nhân ma trận AB xác định, hai ma trận A và B cần thỏa mãn điều kiện cụ thể sau:
- Số cột của ma trận A phải bằng số hàng của ma trận B.
- Kích thước của ma trận A phải được biểu diễn dưới dạng m x n, trong đó m là số hàng và n là số cột.
- Kích thước của ma trận B phải được biểu diễn dưới dạng p x q, trong đó p là số hàng và q là số cột.
- Điều kiện đủ: m = p và q = n
Các tính chất cơ bản của nhân hai ma trận
Phép nhân hai ma trận có một số tính chất quan trọng sau:
- Tính chất giao hoán: Phép nhân ma trận không giao hoán, nghĩa là AB ≠ BA nói chung.
- Tính chất kết hợp: Phép nhân ma trận có tính chất kết hợp, nghĩa là (AB)C = A(BC).
- Tính chất phân phối: Phép nhân ma trận có tính chất phân phối đối với phép cộng, nghĩa là A(B + C) = AB + AC và (B + C)A = BA + CA.
- Tính chất tồn tại phần tử nghịch đảo: Một ma trận vuông A có ma trận nghịch đảo A^(-1) khi và chỉ khi det(A) ≠ 0, với det(A) là định thức của ma trận A. Khi đó, AB = BA = I, với I là ma trận đơn vị.
- (AB)’ = A’B’
- Nếu ma trận A và B là 2 ma trận vuông cùng cấp. Khi đó ta có: |AB|= |A|.|B|
Hướng dẫn chi tiết cách nhân 2 ma trận
Dưới đây là hướng dẫn chi tiết nhân 2 ma trận phổ biến nhất mà các bạn có thể tham khảo:
Cách 1: Sử dụng công thức
Công thức để tính toán phần tử (i, j) của ma trận tích AB là:
$$AB\lbrack i,\;j\rbrack\;=\;\Sigma(A\lbrack i,\;k\rbrack\;\times\;B\lbrack k,\;j\rbrack)$$
Trong đó:
- AB[i, j] là phần tử nằm ở hàng thứ i và cột thứ j của ma trận tích AB.
- Σ là ký hiệu tổng hợp.
- A[i, k] là phần tử nằm ở hàng thứ i và cột thứ k của ma trận A.
- B[k, j] là phần tử nằm ở hàng thứ k và cột thứ j của ma trận B.
- k là biến số chạy từ 1 đến n (số cột của ma trận A).
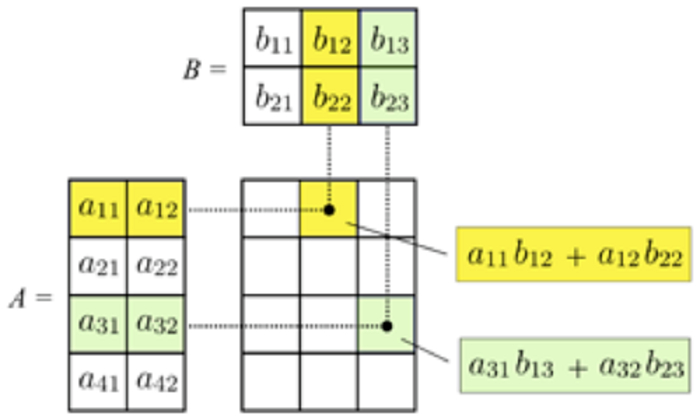
Cách 2: Sử dụng phương pháp chia nhỏ ma trận
Phương pháp chia nhỏ ma trận giúp chia nhỏ phép nhân ma trận thành các tích 2 ma trận đơn giản hơn, dễ tính toán hơn.
Cách nhân ma trận với một số
Nhân ma trận với một số, hay còn gọi là nhân vô hướng ma trận, là một phép toán tuyến tính đơn giản, được thực hiện bằng cách nhân từng phần tử của ma trận với một số thực vô hướng. Cách nhân ma trận A với số thực k được thực hiện theo các bước sau:
- Bước 1: Xác định kích thước của ma trận A: Ma trận A cần có kích thước m x n, với m là số hàng và n là số cột.
- Bước 2: Tạo một ma trận mới B là kết quả của phép nhân, có cùng kích thước với ma trận A.
- Bước 3: Đối với mỗi phần tử aij của ma trận A (nằm ở hàng i và cột j), ta tính giá trị mới bij = k * a_ij.
- Bước 4: Gán giá trị bij cho phần tử tương ứng trong ma trận B.
- Bước 5: Ma trận B thu được chính là kết quả của phép nhân ma trận A với số k.
Ví dụ:
Cho ma trận A:
A = [[1, 2, 3],
[4, 5, 6]]
Và số k = 2.
Nhân ma trận A với số k, ta thu được ma trận B:
B = [[2, 4, 6],
[8, 10, 12]]
Cách nhân 2 ma trận không cùng cấp
Thông thường, phép nhân ma trận chỉ được thực hiện khi hai ma trận có kích thước phù hợp. Tuy nhiên, trong một số trường hợp đặc biệt, ta có thể nhân hai ma trận không cùng cấp bằng cách sử dụng phép nhân Kronecker.
Phép nhân Kronecker là một phép toán kết hợp hai ma trận thành một ma trận mới có kích thước lớn hơn. Phép toán này được ký hiệu là A ⊗ B, với A và B là hai ma trận bất kỳ.
Cách thực hiện phép nhân Kronecker như sau:
- B1: Đặt A là ma trận có kích thước m x n và B là ma trận có kích thước p x q.
- B2: Tạo một ma trận mới C có kích thước mp x nq.
- B3: Đối với mỗi phần tử aij, ta nhân ma trận B với số aij.
- B4: Gán ma trận kết quả thu được vào vị trí tương ứng trong ma trận C.
- B5: Ma trận C thu được chính là kết quả của phép nhân Kronecker A ⊗ B
Ví dụ minh hoạ về cách nhân hai ma trận không cùng cấp:
Cho ma trận A:
A = [[1, 2],
[3, 4]]
Và ma trận B:
B = [[5, 6],
[7, 8]]
Nhân ma trận A với ma trận B bằng phép nhân Kronecker, ta thu được ma trận C như sau:
C = [[5, 6, 10, 12],
[15, 16, 20, 24],
[35, 36, 50, 56],
[45, 48, 60, 64]]

Cách nhân 2 ma trận bằng máy tính cầm tay Casio fx 580VN
Bạn có thể sử dụng máy tính cầm tay Casio để thực hiện phép tính nhân ma trận. Cách làm này vừa đơn giản, độ chính xác cao mà lại tiết kiệm nhiều thời gian. Cách nhân 2 ma trận bằng máy tính Casio được thực hiện theo các bước như sau:
- Bước 1: Nhấn chọn phím “Menu” hoặc “Mode” sau đó nhấn phím 4 để chọn Matrix (Ma trận).
- Bước 2: Chọn phím 1 “MatA” để gán ma trận A vào bộ nhớ MatA, nhập số lần lượt tương ứng với số dòng, sốt cột cần tính của ma trận, sau đó điền đầy đủ các giá trị theo hàng của ma trận A.
- Bước 3: Thực hiện tương tự để gán giá trị ma trận B vào MatB.
- Bước 4: Nhấm phím ONPT sau đó nhấn phím 3 để chọn MatA, nhấn phím “X”, nhấn phím 4 để chọn MatB, sau đó bấm phím “=” rồi chờ máy tính hiển thị kết quả.

Ứng dụng của phép nhân ma trận
Phép nhân 2 ma trận 4×4 hay 3×3… là phép tính toán cơ bản trong môn Đại số & Giải tích, nó có nhiều ứng dụng trong thực tế, bao gồm:
- Giải hệ phương trình tuyến tính: Phép nhân ma trận có thể được sử dụng để giải hệ phương trình tuyến tính bằng phương pháp ma trận.
- Biến đổi hình học: Tích hai ma trận được dùng để mô tả các phép biến đổi hình học như phép tịnh tiến, phép xoay và phép thu phóng.
- Giải mã và mã hóa dữ liệu: Sử dụng trong các thuật toán mã hóa và giải mã dữ liệu như mã hóa RSA.
- Học máy và trí tuệ nhân tạo: Đóng vai trò quan trọng trong các thuật toán học máy và trí tuệ nhân tạo như mạng nơ-ron nhân tạo và học sâu.
Ví dụ minh hoạ về nhân hai ma trận
Dưới đây là một vài ví dụ minh hoạ về phép nhân hai ma trận giúp bạn hiểu rõ hơn về cách làm này:
Ví dụ 1:
Cho hai ma trận:
- A = [[1, 2], [3, 4]]
- B = [[5, 6], [7, 8]]
Tính toán ma trận tích AB.
Giải:
Kích thước của ma trận A là 2 x 2 và kích thước của ma trận B là 2 x 2, thỏa mãn điều kiện để thực hiện phép nhân ma trận.
Sử dụng công thức, ta có:
- AB[1, 1] = (1 x 5) + (2 x 7) = 19
- AB[1, 2] = (1 x 6) + (2 x 8) = 22
- AB[2, 1] = (3 x 5) + (4 x 7) = 43
- AB[2, 2] = (3 x 6) + (4 x 8) = 50
Vậy ma trận tích AB là:
- AB = [[19, 22], [43, 50]]
Ví dụ 2: Nhân 2 ma trận 3×3
Cho hai ma trận:
A = [[1, 2, 3],
[4, 5, 6]]
và
B = [[7, 8, 9],
[10, 11, 12],
[13, 14, 15]]
Giải:
Để nhân hai ma trận A và B, hai ma trận cần có cùng số cột của ma trận thứ nhất bằng số hàng của ma trận thứ hai. Do đó, trong ví dụ này, ta có thể thực hiện phép nhân ma trận A và B.
Sử dụng công thức nhân ma trận, ta có:
C = A x B = [[1, 2, 3] x [7, 10, 13],
[4, 5, 6] x [8, 11, 14],
[4, 5, 6] x [9, 12, 15]]
Tính toán từng phần tử của ma trận C:
- C[1, 1] = 1 x 7 + 2 x 10 + 3 x 13 = 58
- C[1, 2] = 1 x 8 + 2 x 11 + 3 x 14 = 65
- C[1, 3] = 1 x 9 + 2 x 12 + 3 x 15 = 72
- C[2, 1] = 4 x 7 + 5 x 10 + 6 x 13 = 110
- C[2, 2] = 4 x 8 + 5 x 11 + 6 x 14 = 127
- C[2, 3] = 4 x 9 + 5 x 12 + 6 x 15 = 144
Vậy, ma trận kết quả C là:
C = [[58, 65, 72],
[110, 127, 144]]
Ví dụ 3: Nhân ma trận với số
Cho ma trận A:
A = [[1, 2, 3],
[4, 5, 6]]
và số k = 3.
Giải:
Nhân ma trận A với số k, ta thực hiện bằng cách nhân từng phần tử của ma trận A với số k.
B = k x A = [[k x 1, k x 2, k x 3],
[k x 4, k x 5, k x 6]]
Tính toán từng phần tử của ma trận B:
- B[1, 1] = k x 1 = 3
- B[1, 2] = k x 2 = 6
- B[1, 3] = k x 3 = 9
- B[2, 1] = k x 4 = 12
- B[2, 2] = k x 5 = 15
- B[2, 3] = k x 6 = 18
Vậy, ma trận kết quả B là:
B = [[3, 6, 9],
[12, 15, 18]]
Lời kết
Bài viết này của chúng tôi đã cung cấp cho bạn hướng dẫn chi tiết về phép nhân 2 ma trận, bao gồm định nghĩa, điều kiện thực hiện, cách tính toán, các tính chất và ứng dụng. Phép nhân ma trận là một phép toán cơ bản và quan trọng trong Đại số và Giải tích. Hy vọng những thông tin trên đây sẽ hữu ích cho bạn trong việc học tập và nghiên cứu.