Hướng dẫn chi tiết phép chia đa thức một biến và các phương pháp chia hiệu quả

Phép chia đa thức một biến là một công cụ quan trọng trong toán học, giúp tìm thương và số dư khi chia hai đa thức. Qua các phương pháp chia như rút hệ số, chia đặt dọc, hay phương pháp Horner, người học sẽ dễ dàng áp dụng vào các bài tập. Bài viết sẽ cung cấp hướng dẫn chi tiết và ứng dụng thực tế cho học sinh lớp 7.

Phép chia đa thức một biến là phép toán tìm thương và số dư khi chia một đa thức cho một đa thức khác

Trong toán học, đa thức là gì là một biểu thức đại số được tạo thành từ các số và biến số. Phép chia đa thức một biến là một phép toán quan trọng giúp tìm ra thương và số dư khi chia một đa thức cho một đa thức khác.

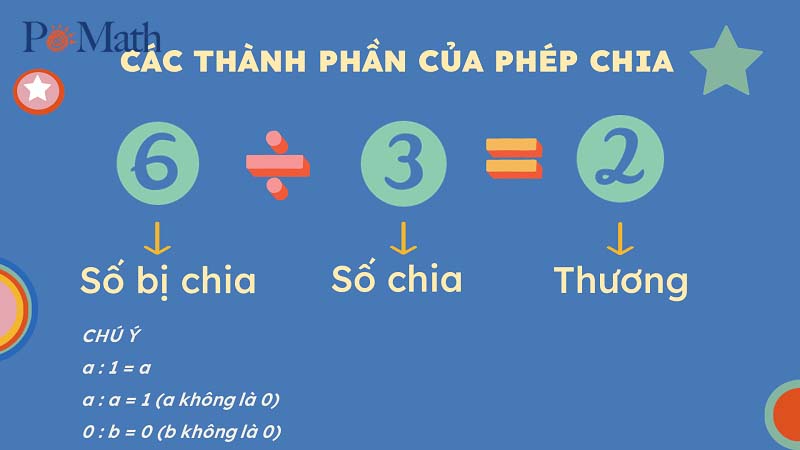
Khi thực hiện chia đa thức, ta sẽ chia đa thức bị chia (dividend) cho đa thức chia (divisor) để tìm ra thương (quotient) và số dư (remainder). Quá trình này tương tự như phép chia số nguyên thông thường, nhưng phức tạp hơn do phải thao tác với các số hạng chứa biến.

Kết quả của phép chia đa thức luôn tuân theo công thức: Đa thức bị chia = (Đa thức chia × Thương) + Số dư. Trong đó bậc của số dư luôn nhỏ hơn bậc của đa thức chia. Điều này giúp ta có thể kiểm tra lại kết quả phép chia và đảm bảo tính chính xác của phép tính.

Các phương pháp thực hiện phép chia đa thức một biến trong toán học

Phép chia đa thức một biến là một trong những phép tính quan trọng khi học về đa thức. Để thực hiện phép chia này, có 3 phương pháp chính được sử dụng phổ biến. Mỗi phương pháp có những ưu điểm và phù hợp với từng dạng bài toán khác nhau.

Việc nắm vững các phương pháp chia đa thức giúp giải quyết nhiều bài toán phức tạp. Trước khi thực hiện phép chia, cần nắm rõ phép nhân đa thức một biến để có thể kiểm tra kết quả sau khi chia.

Phương pháp chia đa thức bằng cách rút hệ số

Phương pháp rút hệ số thường được áp dụng khi đa thức có dạng đơn giản hoặc có thể phân tích thành tích các nhân tử. Phương pháp này giúp rút gọn quá trình tính toán và cho kết quả nhanh chóng.

Khi thực hiện, ta cần phân tích đa thức bị chia và đa thức chia thành các nhân tử, sau đó rút gọn các hệ số giống nhau. Phương pháp này đặc biệt hiệu quả khi đa thức có chứa các biểu thức bình phương hoặc lập phương.

Phương pháp chia đa thức bằng phép chia đặt dọc

Phép chia đặt dọc là phương pháp truyền thống và phổ biến nhất. Phương pháp này thực hiện theo các bước tương tự như phép chia số học thông thường, nhưng áp dụng cho các đa thức.

Để thực hiện chính xác, cần sắp xếp các số hạng theo thứ tự giảm dần của số mũ. Sau đó, lần lượt thực hiện phép nhân và phép trừ cho đến khi được thương số và số dư (nếu có).

Phương pháp này tuy mất nhiều thời gian hơn nhưng lại rất trực quan và dễ kiểm tra lại kết quả.

Phương pháp Horner để chia đa thức một biến

Phương pháp Horner là một cách tiếp cận hiệu quả và nhanh chóng để thực hiện phép chia đa thức cho một đơn thức bậc nhất. Phương pháp này được William George Horner phát triển vào đầu thế kỷ 19.

Ưu điểm của phương pháp Horner là giảm thiểu số phép tính cần thực hiện. Thay vì phải thực hiện nhiều phép nhân và cộng phức tạp, ta chỉ cần thực hiện một chuỗi các phép nhân và cộng đơn giản.

Phương pháp này đặc biệt hữu ích khi cần tính giá trị của đa thức tại một điểm cụ thể hoặc khi cần phân tích đa thức thành tích các nhân tử tuyến tính.

Hướng dẫn chi tiết cách chia đa thức một biến cho đa thức bậc nhất và bậc hai

Việc chia đa thức là một kỹ năng toán học quan trọng giúp giải quyết nhiều bài toán phức tạp. Hướng dẫn chia đa thức cần tuân theo các nguyên tắc cơ bản và thực hiện theo trình tự logic. Phép chia đa thức có thể áp dụng cho nhiều dạng khác nhau như chia cho đơn thức, nhị thức bậc nhất hay tam thức bậc hai.

Để thực hiện chia đa thức đơn giản, cần nắm vững các quy tắc cơ bản và thực hành nhiều. Tương tự như phép đổi cận tích phân, việc chia đa thức đòi hỏi sự cẩn thận và chính xác trong từng bước tính.

Các bước chia đa thức cho đơn thức

Khi chia đa thức cho đơn thức, bước đầu tiên là sắp xếp các số hạng của đa thức theo thứ tự giảm dần của số mũ. Điều này giúp việc tính toán trở nên có hệ thống và dễ kiểm soát hơn.

Tiếp theo, lấy từng số hạng của đa thức chia cho đơn thức. Quá trình này tuân theo quy tắc chia số mũ và hệ số. Kết quả thu được sẽ là một đa thức mới có bậc thấp hơn đa thức ban đầu.

Cuối cùng, kiểm tra lại kết quả bằng cách nhân thương số với số chia. Nếu kết quả trùng với số bị chia ban đầu thì phép tính đã chính xác.

Quy tắc chia đa thức cho nhị thức bậc nhất

Phương pháp Ruffini là công cụ hiệu quả để chia đa thức cho nhị thức bậc nhất ax + b. Phương pháp này giúp rút ngắn thời gian tính toán và giảm thiểu sai sót.

Khi áp dụng phương pháp này, cần sắp xếp các hệ số của đa thức theo thứ tự giảm dần của số mũ. Nếu có số hạng nào thiếu, điền số 0 vào vị trí tương ứng.

Quá trình tính toán được thực hiện theo ma trận, giúp theo dõi các bước một cách trực quan. Kết quả cuối cùng sẽ cho ta thương số và số dư của phép chia.

Phương pháp chia đa thức cho tam thức bậc hai

Chia đa thức cho tam thức bậc hai đòi hỏi kỹ năng phân tích và tổng hợp tốt. Trước tiên, cần kiểm tra xem tam thức bậc hai có phân tích được thành nhân tử hay không.

Nếu tam thức bậc hai phân tích được thành tích các nhân tử bậc nhất, có thể áp dụng phương pháp chia lần lượt cho từng nhân tử. Cách này giúp đơn giản hóa quá trình tính toán.

Trong trường hợp không phân tích được, sử dụng phương pháp chia đa thức tổng quát. Phương pháp này tuy phức tạp hơn nhưng cho kết quả chính xác và áp dụng được cho mọi trường hợp.

Bài tập thực hành phép chia đa thức một biến từ cơ bản đến nâng cao

Phép chia đa thức là một trong những kỹ năng toán học quan trọng giúp học sinh rèn luyện tư duy logic và khả năng tính toán. Việc thực hành nhiều bài tập sẽ giúp nắm vững kiến thức và áp dụng linh hoạt vào các bài toán phức tạp hơn.

Tương tự như phép chia số học, phép chia đa thức một biến lớp 7 cũng tuân theo các quy tắc nhất định về bậc đa thức và hệ số. Việc nắm vững các quy tắc này sẽ giúp học sinh giải nhanh và chính xác các dạng bài tập khác nhau.

Để giải thành thạo các bài tập chia đa thức, học sinh cần thực hành từ những bài tập cơ bản đến các bài tập nâng cao, tương tự như cách xây dựng khối đa diện đều từ những khối cơ bản.

Bài tập chia đa thức một biến lớp 7 có lời giải

Khi giải các bài tập chia đa thức, bước đầu tiên là xác định bậc của đa thức bị chia và đa thức chia. Điều này giúp dự đoán được bậc của thương và số phép tính cần thực hiện.

Tiếp theo, cần sắp xếp các số hạng theo thứ tự giảm dần của số mũ biến. Việc sắp xếp này giúp quá trình chia được thuận lợi và tránh sai sót trong tính toán.

Cuối cùng, thực hiện phép chia theo thuật toán đã học, ghi nhận kết quả từng bước một cách cẩn thận. Kiểm tra lại kết quả bằng cách nhân thương với số chia và cộng với số dư.

Bài tập nâng cao về phép chia đa thức

Các bài tập nâng cao thường yêu cầu vận dụng tổng hợp nhiều kiến thức và kỹ năng. Chẳng hạn như kết hợp phép chia với phân tích đa thức thành nhân tử.

Một số bài tập đòi hỏi phải biến đổi về dạng đa thức chuẩn trước khi thực hiện phép chia. Quá trình này giúp rèn luyện kỹ năng biến đổi đại số và tư duy logic.

Ngoài ra, có những bài tập yêu cầu tìm điều kiện để phép chia có số dư bằng 0 hoặc thương có dạng đặc biệt. Đây là dạng bài khó, cần nắm vững lý thuyết và có nhiều kinh nghiệm giải.

Các dạng bài tập thường gặp và cách giải

Dạng 1: Chia đa thức có một biến theo thuật toán cơ bản. Cần thực hiện từng bước theo quy trình, ghi chép cẩn thận để tránh sai sót trong tính toán.

Dạng 2: Tìm thương và số dư khi biết đa thức bị chia và đa thức chia. Áp dụng công thức phân chia với số dư, kiểm tra kết quả bằng cách thế các giá trị cụ thể.

Dạng 3: Tìm điều kiện để phép chia có số dư cho trước. Phương pháp giải là lập phương trình từ điều kiện đã cho, sau đó giải phương trình để tìm các tham số.

Ứng dụng của phép chia đa thức một biến trong giải toán và thực tế

Phép chia đa thức một biến có nhiều ứng dụng quan trọng trong toán học và đời sống. Việc thực hiện phép chia đa thức giúp giải quyết nhiều bài toán phức tạp, từ phân tích đa thức đến tìm nghiệm của phương trình.

Các ứng dụng chia đa thức không chỉ giới hạn trong phạm vi toán học thuần túy mà còn mở rộng sang nhiều lĩnh vực khác như kỹ thuật, kinh tế và khoa học máy tính. Việc nắm vững công thức chia đa thức là nền tảng để giải quyết các bài toán phức tạp hơn.

Ứng dụng trong phân tích đa thức thành nhân tử

Phép chia đa thức đóng vai trò then chốt trong việc phân tích đa thức thành nhân tử. Khi chia một đa thức cho một đa thức bậc thấp hơn, ta có thể xác định được các nhân tử của đa thức ban đầu.

Trong trường hợp đa thức có nghiệm hữu tỷ, việc sử dụng phép chia với phương pháp Horner giúp tìm ra các nghiệm một cách hiệu quả. Quá trình này đặc biệt hữu ích khi làm việc với đa thức bậc cao.

Ứng dụng trong giải phương trình đa thức

Khi giải phương trình đa thức, phép chia giúp đơn giản hóa biểu thức và tìm nghiệm. Nếu biết một nghiệm của phương trình, ta có thể chia đa thức cho x – a (với a là nghiệm) để giảm bậc của phương trình.

Phương pháp này đặc biệt hiệu quả khi kết hợp với định lý Viète và các phương pháp giải phương trình khác. Việc giảm bậc phương trình giúp bài toán trở nên đơn giản và dễ giải quyết hơn.

Ứng dụng trong các bài toán thực tế

Trong lĩnh vực kỹ thuật, phép chia đa thức được sử dụng để tính toán các đặc trưng của mạch điện. Ví dụ, khi phân tích hàm truyền đạt của mạch điện, các kỹ sư thường phải thực hiện phép chia đa thức để xác định các cực và không điểm.

Trong kinh tế, phép chia đa thức giúp mô hình hóa và dự báo xu hướng thị trường. Các nhà phân tích sử dụng đa thức để xấp xỉ đường cong cung cầu, sau đó thực hiện các phép chia để tìm điểm cân bằng và dự đoán biến động giá.

Trong lĩnh vực máy học, thuật toán hồi quy đa thức sử dụng phép chia để tối ưu hóa mô hình và giảm thiểu sai số. Điều này cho phép máy tính có thể học và dự đoán các xu hướng phức tạp từ dữ liệu thực tế.

Phép chia đa thức một biến là một khái niệm quan trọng trong toán học, giúp giải quyết nhiều bài toán khác nhau. Nắm vững cách thực hiện các phương pháp chia khác nhau như rút hệ số hay phép chia đặt dọc sẽ giúp bạn không chỉ hoàn thành tốt các bài tập, mà còn ứng dụng hiệu quả trong việc phân tích đa thức hay giải phương trình. Hãy bắt tay vào thực hành để ghi nhớ và tự tin hơn với kiến thức này!