Quy tắc L’Hospital và các phương pháp tính giới hạn dạng vô định hiệu quả

Quy tắc L’Hospital là một phương pháp hữu ích giúp bạn tính giới hạn dạng vô định bằng đạo hàm. Bài viết này sẽ hướng dẫn chi tiết cách áp dụng quy tắc này, các lưu ý quan trọng và ví dụ minh họa cụ thể để bạn có thể dễ dàng nắm vững kiến thức và ứng dụng hiệu quả trong giải toán giới hạn.

Quy tắc L’Hospital là phương pháp tính giới hạn dạng vô định bằng đạo hàm

Quy tắc l’hospital là một phương pháp toán học quan trọng được sử dụng để tính giới hạn của các biểu thức dạng vô định. Phương pháp này do nhà toán học người Pháp Guillaume de l’Hôpital phát triển vào thế kỷ 17, dựa trên công trình nghiên cứu của Johann Bernoulli.

Khi áp dụng quy tắc lopitan, ta có thể tính được giới hạn của một tỉ số mà cả tử số và mẫu số đều tiến đến 0 hoặc vô cùng. Nguyên lý cơ bản là lấy đạo hàm của cả tử số và mẫu số, sau đó tính giới hạn của tỉ số mới. Nếu kết quả vẫn là dạng vô định, có thể tiếp tục áp dụng quy tắc này cho đến khi thu được kết quả xác định.

Việc áp dụng l’Hôpital’s rule đòi hỏi các hàm số phải khả vi và thỏa mãn một số điều kiện nhất định. Đây là công cụ mạnh mẽ giúp giải quyết nhiều bài toán phức tạp trong giải tích, đặc biệt là các bài toán liên quan đến giới hạn dạng vô định 0/0 và ∞/∞. Phương pháp này cũng có thể mở rộng để tính các dạng vô định khác như 0.∞, ∞-∞, 1∞, 00, ∞0 thông qua việc biến đổi về dạng tỉ số.

Các điều kiện cần và đủ để

Việc áp dụng quy tắc l’hospital đòi hỏi phải thỏa mãn một số điều kiện nghiêm ngặt để đảm bảo kết quả chính xác. Trước khi áp dụng quy tắc này, cần kiểm tra kỹ các điều kiện về dạng vô định của biểu thức và tính khả vi của các hàm số.

Điều kiện đầu tiên là biểu thức cần tính giới hạn phải ở dạng vô định. Cụ thể, biểu thức phải thuộc một trong các dạng 0/0 hoặc ∞/∞. Các dạng vô định khác như ∞-∞, 0.∞, 1^∞, ∞^0, 0^0 cần được chuyển về dạng 0/0 hoặc ∞/∞ bằng cách quy tắc phá ngoặc đổi dấu hoặc logarit hóa trước khi áp dụng.

Điều kiện thứ hai là các hàm số tử số và mẫu số phải khả vi tại điểm cần tính giới hạn hoặc trong lân cận của điểm đó (trừ chính điểm đang xét). Đạo hàm của mẫu số không được bằng 0 tại điểm đang xét, nếu không sẽ dẫn đến việc phải áp dụng quy tắc nhiều lần.

Ngoài ra, giới hạn của tỉ số các đạo hàm phải tồn tại (hữu hạn hoặc vô cực). Nếu tỉ số đạo hàm vẫn ở dạng vô định, có thể áp dụng quy tắc L’Hospital tiếp tục cho đến khi thu được kết quả xác định. Tuy nhiên cần lưu ý rằng việc áp dụng nhiều lần không phải lúc nào cũng cho kết quả đúng.

Phương pháp tính giới hạn dạng vô định bằng quy tắc L’Hospital

Quy tắc l’hospital là một công cụ mạnh mẽ để tính giới hạn của các biểu thức dạng vô định. Phương pháp này cho phép chuyển đổi việc tính giới hạn của một tỉ số thành tỉ số của các đạo hàm, giúp đơn giản hóa quá trình tính toán.

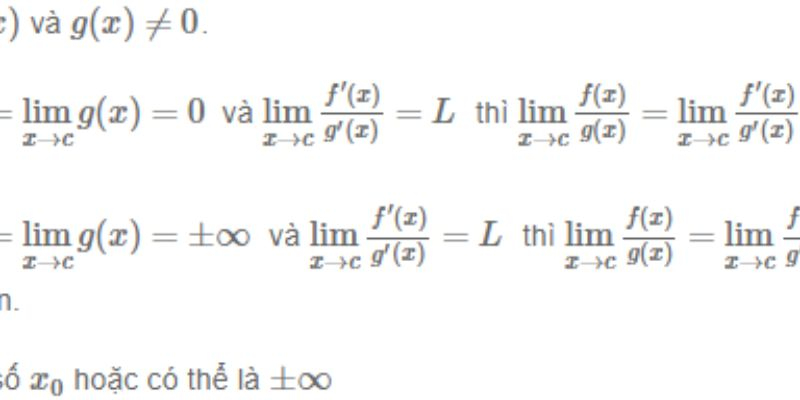
Phương pháp này đặc biệt hiệu quả khi xử lý các dạng vô định phổ biến như 0/0 và ∞/∞. Việc áp dụng derivatives and limits theo quy tắc này giúp biến đổi biểu thức ban đầu thành dạng có thể tính được.

Tuy nhiên, cần lưu ý rằng phương pháp này chỉ áp dụng được khi biểu thức thỏa mãn các điều kiện nhất định về tính liên tục và khả vi của các hàm số. Việc evaluating limits cần được thực hiện cẩn thận và tuân thủ đúng các bước.

Các bước áp dụng quy tắc L’Hospital

Bước đầu tiên là xác định dạng vô định của biểu thức cần tính giới hạn. Điều này giúp đảm bảo việc áp dụng quy tắc L’Hospital là phù hợp và cần thiết.

Tiếp theo, ta tính đạo hàm của cả tử số và mẫu số theo biến độc lập. Quá trình này có thể được lặp lại nhiều lần nếu kết quả vẫn là dạng vô định.

Cuối cùng, thay giá trị điểm cần tính giới hạn vào biểu thức đã đạo hàm. Nếu kết quả vẫn là dạng vô định, tiếp tục áp dụng quy tắc cho đến khi thu được kết quả xác định.

Ví dụ minh họa cách tính giới hạn dạng 0/0

Xét ví dụ tính giới hạn của biểu thức (ex – 1 – x)/x2 khi x tiến đến 0. Đây là dạng vô định 0/0 vì khi thế x = 0, cả tử và mẫu đều bằng 0.

Áp dụng quy tắc L’Hospital lần 1, ta lấy đạo hàm tử số và mẫu số:
Tử số: đạo hàm của (ex – 1 – x) = ex – 1
Mẫu số: đạo hàm của x2 = 2x

Khi x tiến đến 0, biểu thức (ex – 1)/2x vẫn cho dạng 0/0. Tiếp tục áp dụng quy tắc một lần nữa, ta được kết quả cuối cùng là 1/2.

Ví dụ minh họa cách tính giới hạn dạng ∞/∞

Khi tính giới hạn của biểu thức (x2 + x)/(x2 – 1) khi x tiến đến vô cùng, ta có dạng vô định ∞/∞. Đây là trường hợp điển hình cần áp dụng quy tắc L’Hospital.

Lấy đạo hàm tử số và mẫu số:
Tử số: đạo hàm của (x2 + x) = 2x + 1
Mẫu số: đạo hàm của (x2 – 1) = 2x

Khi x tiến đến vô cùng, biểu thức (2x + 1)/2x có thể viết lại thành 1 + 1/2x. Khi x tiến đến vô cùng, 1/2x tiến đến 0, nên giới hạn của biểu thức ban đầu bằng 1.

Những lưu ý quan trọng khi sử dụng định lý L’Hospital để tính giới hạn

Việc áp dụng quy tắc l’hospital đòi hỏi sự cẩn trọng và hiểu biết sâu sắc về các điều kiện tiên quyết. Khi đối mặt với các dạng giới hạn vô định hoặc vô cùng, việc nắm vững các nguyên tắc cơ bản sẽ giúp tránh được những sai lầm phổ biến.

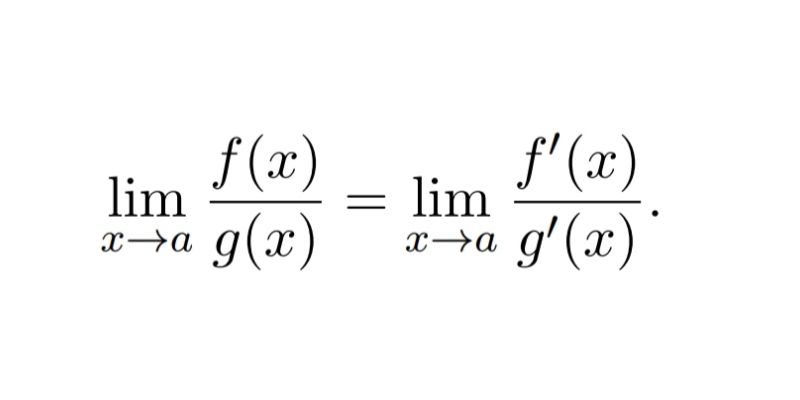
Một trong những yếu tố then chốt là phải đảm bảo biểu thức đang xét thỏa mãn dạng vô định hoặc vô cùng trước khi áp dụng định lý l’hospital. Nhiều trường hợp học sinh vội vàng lấy đạo hàm mà không kiểm tra điều kiện ban đầu, dẫn đến kết quả sai.

Theo Học Thế Nào VN, việc áp dụng đúng các kỹ thuật calculus techniques không chỉ giúp giải quyết bài toán nhanh chóng mà còn đảm bảo độ chính xác cao. Điều quan trọng là phải kiểm tra xem liệu có thể đơn giản hóa biểu thức trước khi áp dụng quy tắc hay không.

Các sai lầm thường gặp khi áp dụng quy tắc L’Hospital

Sai lầm phổ biến nhất là áp dụng quy tắc khi biểu thức không ở dạng vô định hoặc vô cùng. Nhiều học sinh máy móc lấy đạo hàm tử số và mẫu số mà không kiểm tra điều kiện tiên quyết.

Một lỗi khác là bỏ qua các bước đơn giản hóa biểu thức trước khi áp dụng quy tắc. Trong nhiều trường hợp, việc rút gọn hoặc phân tích thừa số có thể giúp tìm được giới hạn dễ dàng hơn mà không cần sử dụng L’Hospital.

Ngoài ra, việc lấy đạo hàm không chính xác hoặc bỏ sót các thành phần trong biểu thức cũng là nguyên nhân dẫn đến kết quả sai. Đặc biệt với các biểu thức phức tạp, cần phải thực hiện từng bước một cách cẩn thận và có hệ thống.

Cách khắc phục và tránh sai sót

Trước khi áp dụng quy tắc, cần xác định rõ dạng giới hạn đang xét. Kiểm tra kỹ lưỡng xem biểu thức có thực sự ở dạng vô định hay vô cùng không. Nếu không thuộc hai dạng này, tìm phương pháp khác phù hợp hơn.

Việc rèn luyện kỹ năng tính đạo hàm và nắm vững các công thức cơ bản là vô cùng quan trọng. Thực hành nhiều bài tập đa dạng sẽ giúp phát triển trực giác toán học và khả năng nhận diện các trường hợp đặc biệt.

Khi giải bài toán, nên chia nhỏ quá trình thành các bước: kiểm tra điều kiện, đơn giản hóa biểu thức nếu có thể, áp dụng quy tắc một cách có hệ thống, và cuối cùng là kiểm tra lại kết quả. Cách làm này giúp giảm thiểu sai sót và tăng độ chính xác.

Ứng dụng quy tắc L’Hospital trong việc giải các bài toán phức tạp

Việc áp dụng quy tắc l’hospital đóng vai trò then chốt trong việc giải quyết các bài toán giới hạn phức tạp. Phương pháp này không chỉ giúp đơn giản hóa các biểu thức rắc rối mà còn mang lại cách tiếp cận có hệ thống để xử lý nhiều dạng giới hạn khác nhau.

Khi gặp các bài toán về continuity and limits, việc kết hợp nhiều kỹ thuật tính giới hạn là điều không thể tránh khỏi. Quy tắc L’Hospital thường được áp dụng sau khi đã thử các phương pháp cơ bản như khử, thay thế biến số hay phân tích thành nhân tử.

Đối với người mới học toán, mathematics for beginners cần nắm vững các điều kiện áp dụng quy tắc L’Hospital. Điều này giúp tránh việc lạm dụng quy tắc một cách không cần thiết và đảm bảo kết quả chính xác khi giải toán.

Kết hợp quy tắc L’Hospital với các phương pháp khác

Việc kết hợp quy tắc L’Hospital với các phương pháp khác tạo nên công cụ mạnh mẽ trong việc simplifying limits. Phương pháp này thường được sử dụng song song với kỹ thuật logarit hóa để giải quyết các dạng giới hạn mũ.

Trong nhiều trường hợp, việc áp dụng quy tắc L’Hospital đơn thuần không đủ để giải quyết bài toán. Cần phải kết hợp với các phép biến đổi đại số, lượng giác hoặc các định lý giới hạn cơ bản khác để đạt được kết quả mong muốn.

Kinh nghiệm cho thấy việc nhận biết thời điểm thích hợp để chuyển đổi giữa các phương pháp là yếu tố quyết định sự thành công trong giải toán giới hạn. Điều này đòi hỏi sự linh hoạt và tư duy sáng tạo từ người giải.

Bài tập mẫu và hướng dẫn giải chi tiết

Xét ví dụ tính giới hạn: lim(x→0) (sin(x) – x)/(x³). Đầu tiên, nhận thấy đây là dạng 0/0 nên có thể áp dụng quy tắc L’Hospital. Sau khi đạo hàm tử số và mẫu số, ta được: lim(x→0) (cos(x) – 1)/(3x²).

Kết quả vẫn ở dạng 0/0 nên tiếp tục áp dụng quy tắc L’Hospital lần thứ hai. Đạo hàm tiếp, ta có: lim(x→0) (-sin(x))/(6x). Một lần nữa áp dụng quy tắc L’Hospital cho ra kết quả cuối cùng là -1/6.

Qua bài tập mẫu trên, có thể thấy việc áp dụng quy tắc L’Hospital nhiều lần là cần thiết để đạt được kết quả. Điều quan trọng là phải kiểm tra kỹ điều kiện áp dụng ở mỗi bước và thực hiện các phép đạo hàm một cách chính xác.

Khi học toán, quy tắc L’Hospital trở thành một công cụ đắc lực để giải quyết các giới hạn dạng vô định. Bài viết đã trình bày một cách chi tiết về điều kiện áp dụng, các bước thực hiện cùng với ví dụ minh họa để bạn dễ dàng vận dụng trong thực tế. Hãy áp dụng quy tắc này để nâng cao kỹ năng giải toán và tìm hiểu thêm về các phương pháp tính giới hạn hiệu quả khác.