Hướng dẫn cách tính số đường chéo của đa giác và ứng dụng trong toán học

Số đường chéo của đa giác là một khái niệm quan trọng trong hình học, giúp xác định mối quan hệ giữa các đỉnh của đa giác. Bài viết sẽ cung cấp công thức và hướng dẫn cụ thể để tính số đường chéo, áp dụng hiệu quả trong các bài tập. Hãy cùng khám phá và nâng cao kiến thức hình học của bạn!

Số đường chéo của đa giác là gì và cách xác định trong hình học phẳng

Số đường chéo của đa giác là tổng số các đoạn thẳng nối hai đỉnh không kề nhau của đa giác đó. Đường chéo có vai trò quan trọng trong việc phân chia đa giác thành các tam giác để tính diện tích hoặc chứng minh các tính chất hình học.

Để xác định số đường chéo của một đa giác n cạnh, ta áp dụng công thức: d = n(n-3)/2, trong đó d là số đường chéo và n là số cạnh của đa giác. Công thức này được rút ra từ việc phân tích số cách chọn 2 đỉnh bất kỳ trong n đỉnh của đa giác, sau đó loại bỏ số cạnh của đa giác ban đầu.

Đường chéo trong hình học đóng vai trò then chốt trong nhiều bài toán phức tạp. Ví dụ, khi cần chia một đa giác thành các tam giác để tính diện tích, ta thường vẽ các đường chéo từ một đỉnh đến các đỉnh không kề với nó. Số tam giác thu được sẽ bằng (n-2), với n là số cạnh của đa giác. Điều này giúp đơn giản hóa việc tính toán diện tích của các đa giác phức tạp.

Một ứng dụng thực tế của đường chéo là trong thiết kế kiến trúc, nơi các thanh giằng chéo được sử dụng để gia cố kết cấu công trình. Theo Viện Kiến trúc Quốc gia, việc bố trí các thanh giằng theo đường chéo giúp tăng độ cứng và khả năng chịu lực của công trình, đặc biệt là với các tòa nhà cao tầng.

Công thức tính số đường chéo của đa giác và cách áp dụng hiệu quả

Để tính số đường chéo của một đa giác, cần dựa vào tính chất hình đa giác và số đỉnh của nó. Công thức tính số đường chéo của đa giác được xác định dựa trên mối quan hệ giữa số đỉnh và số cạnh của đa giác đó.

Khi áp dụng cách tính số đường chéo của đa giác, ta cần nắm vững công thức cơ bản và thực hiện theo trình tự các bước logic. Điều này giúp việc tính toán trở nên chính xác và hiệu quả hơn.

Phương pháp tính số đường chéo dựa trên số đỉnh của đa giác

Công thức tổng quát để tính số đường chéo của một đa giác n cạnh là: d = [n(n-3)]/2, trong đó d là số đường chéo và n là số đỉnh của đa giác. Công thức này được xây dựng dựa trên nguyên lý từ mỗi đỉnh của đa giác có thể kẻ được đường chéo đến tất cả các đỉnh khác, trừ đi 2 đỉnh kề với nó.

Việc áp dụng công thức trên cần chú ý rằng số đỉnh của đa giác phải lớn hơn hoặc bằng 4, vì tam giác không có đường chéo. Đồng thời, kết quả tính toán luôn là số nguyên dương.

Các bước áp dụng công thức tính số đường chéo

Bước đầu tiên là xác định chính xác số đỉnh của đa giác. Điều này có thể thực hiện bằng cách đếm số cạnh hoặc số đỉnh của hình.

Tiếp theo, thay số đỉnh vào công thức [n(n-3)]/2. Việc tính toán nên được thực hiện theo thứ tự: nhân n với (n-3) trước, sau đó chia cho 2.

Cuối cùng, kiểm tra kết quả bằng cách vẽ thử các đường chéo trên hình vẽ để đảm bảo tính chính xác của phép tính.

Ví dụ minh họa cách tính số đường chéo

Lấy ví dụ với hình lục giác (6 cạnh):

• Số đỉnh n = 6
• Áp dụng công thức: d = [6(6-3)]/2 = [6×3]/2 = 18/2 = 9

Với hình bát giác (8 cạnh):

• Số đỉnh n = 8
• Áp dụng công thức: d = [8(8-3)]/2 = [8×5]/2 = 40/2 = 20

Các kết quả này có thể được kiểm chứng bằng cách vẽ thực tế hoặc sử dụng phần mềm đồ họa. Việc thực hành nhiều ví dụ sẽ giúp nắm vững cách áp dụng công thức và tránh sai sót trong quá trình tính toán.

Phân tích số đường chéo trong các đa giác đặc biệt thường gặp

Việc xác định số đường chéo của đa giác là một kỹ năng quan trọng trong hình học. Mỗi loại đa giác đặc biệt sẽ có những đặc điểm riêng về số lượng và vị trí của đường chéo. Để hiểu rõ hơn, ta sẽ phân tích chi tiết từng trường hợp cụ thể.

Số đường chéo trong hình chữ nhật và hình vuông

Trong hình chữ nhật và hình vuông, số đường chéo hình chữ nhật luôn là 2 đường chéo cắt nhau tại tâm của hình. Đường chéo trong hai hình này có tính chất đặc biệt là bằng nhau về độ dài và chia đôi lẫn nhau. Với hình vuông, hai đường chéo còn vuông góc với nhau.

Đường chéo trong hình chữ nhật và hình vuông đóng vai trò quan trọng trong việc xác định tâm đối xứng. Chúng tạo thành 4 tam giác bằng nhau khi cắt nhau, giúp chứng minh nhiều tính chất hình học khác.

Số đường chéo trong hình thoi và hình bình hành

Số đường chéo hình thoi cũng là 2 đường, tương tự như hình chữ nhật. Tuy nhiên, đặc điểm của đường chéo trong hình thoi là chúng vuông góc với nhau và phân chia hình thoi thành 4 tam giác cân bằng nhau. cách tính đường chéo hình tam giác cân có thể áp dụng để tính độ dài các phần được chia bởi đường chéo.

Với hình bình hành, hai đường chéo không vuông góc với nhau nhưng vẫn chia đôi lẫn nhau tại điểm giao. Điểm giao của hai đường chéo chính là tâm đối xứng của hình bình hành.

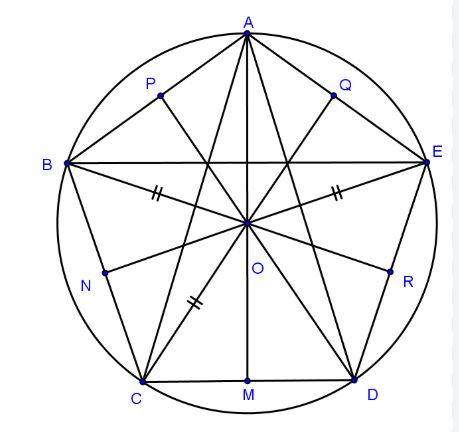
Số đường chéo trong hình ngũ giác đều

Hình ngũ giác đều có 5 đỉnh và mỗi đỉnh có thể nối với 2 đỉnh không kề với nó. Do đó, từ mỗi đỉnh có thể kẻ được 2 đường chéo. Tổng số đường chéo trong hình ngũ giác đều là 5 đường.

Các đường chéo trong hình ngũ giác đều tạo thành một hình sao năm cánh đều đặn. Chúng chia hình ngũ giác thành các tam giác bằng nhau và có vai trò quan trọng trong việc xác định tỷ lệ vàng trong toán học và nghệ thuật.

Các phương pháp tính nhanh số đường chéo đa giác trong bài tập

Việc tính số đường chéo của đa giác là một kỹ năng quan trọng trong hình học. Phương pháp cơ bản nhất là sử dụng công thức d = n(n-3)/2, trong đó n là số cạnh của đa giác. Tuy nhiên, có nhiều cách tiếp cận khác nhau giúp tính toán nhanh chóng và chính xác hơn.

Một phương pháp hiệu quả là vẽ sơ đồ minh họa để tính số đường chéo của đa giác. Bằng cách vẽ các đường chéo từ một đỉnh, ta có thể dễ dàng đếm số đường chéo và kiểm chứng kết quả. Phương pháp này đặc biệt hữu ích với các đa giác có số cạnh nhỏ.

Ngoài ra, việc phân tích các quy luật về công thức đường chéo đa giác cũng giúp giải quyết bài toán nhanh hơn. Chẳng hạn, với mỗi đỉnh của đa giác n cạnh, ta có thể kẻ (n-3) đường chéo, và tổng số đường chéo sẽ bằng n(n-3)/2.

Mẹo nhớ công thức tính số đường chéo

Để nhớ công thức một cách dễ dàng, có thể liên hệ với các hình đa giác quen thuộc. Ví dụ với hình ngũ giác, từ mỗi đỉnh có thể kẻ 2 đường chéo, vậy tổng số đường chéo là 5×2/2=5, phù hợp với công thức d=5(5-3)/2=5.

Một cách khác là ghi nhớ quy luật: số đường chéo luôn bằng tích của số cạnh và (số cạnh trừ 3), chia cho 2. Điều này giúp áp dụng nhanh cho mọi đa giác mà không cần nhớ công thức phức tạp.

Cách kiểm tra kết quả tính số đường chéo

Phương pháp kiểm tra đơn giản nhất là vẽ hình và đếm trực tiếp số đường chéo. Tuy nhiên, với đa giác có nhiều cạnh, cần áp dụng các phương pháp kiểm tra khác như:

• So sánh với kết quả của đa giác có số cạnh liền kề
• Kiểm tra tính hợp lý của kết quả dựa vào tính chất đường chéo
• Áp dụng công thức theo nhiều cách khác nhau

Bài tập vận dụng về số đường chéo đa giác

Bài tập 1: Một đa giác đều có 35 đường chéo. Tìm số cạnh của đa giác.
Giải: Áp dụng công thức d = n(n-3)/2 = 35
=> n(n-3) = 70
=> n2 – 3n – 70 = 0
=> n = 10 (loại n = -7 vì số cạnh phải dương)

Bài tập 2: Chứng minh rằng số đường chéo của một đa giác lồi luôn là số nguyên.
Giải: Do n là số nguyên và công thức d = n(n-3)/2 luôn cho kết quả là số nguyên (vì n và n-3 cùng chẵn hoặc cùng lẻ).

Ứng dụng của số đường chéo trong các bài toán hình học phức tạp

Việc nắm vững cách tính số đường chéo đa giác giúp giải quyết nhiều bài toán hình học phức tạp. Các đường chéo không chỉ là những đoạn thẳng nối các đỉnh không liền kề, mà còn tạo nên những mối quan hệ hình học đặc biệt.

Tổng số đường chéo đa giác có vai trò quan trọng trong việc phân chia đa giác thành các tam giác, từ đó tính được diện tích và các yếu tố hình học khác. Khi áp dụng cách tính đường chéo đa giác, ta có thể giải quyết nhiều dạng bài tập từ cơ bản đến nâng cao.

Bài toán về giao điểm của các đường chéo

Giao điểm của các đường chéo tạo nên những điểm đặc biệt trong đa giác. Trong đa giác đều, các giao điểm này thường nằm trên các đường tròn đồng tâm với tâm của đa giác.

Một ví dụ điển hình là trong lục giác đều, 9 giao điểm của các đường chéo chính nằm trên 3 đường tròn đồng tâm. Theo nghiên cứu của GS. John Conway, tỷ số bán kính của các đường tròn này tuân theo một quy luật toán học nghiêm ngặt.

Việc xác định vị trí các giao điểm còn giúp tìm ra các tâm đối xứng và trục đối xứng của đa giác, từ đó phát hiện nhiều tính chất hình học thú vị khác.

Bài toán về góc tạo bởi các đường chéo

Các góc được tạo bởi đường chéo có mối liên hệ chặt chẽ với góc của đa giác ban đầu. Trong đa giác đều, các góc này thường bằng nhau hoặc bổ túc cho nhau.

Khi nghiên cứu về góc giữa các đường chéo, cần chú ý đến hai loại góc chính:

• Góc giữa hai đường chéo bất kỳ
• Góc giữa đường chéo và cạnh của đa giác

Những mối quan hệ về góc này đặc biệt hữu ích trong việc chứng minh tính chất đồng dạng và tương tự của các tam giác được tạo thành.

Bài toán về diện tích tạo bởi các đường chéo

Các đường chéo chia đa giác thành nhiều phần có diện tích khác nhau. Trong hình vuông, đường chéo chia thành hai tam giác bằng nhau. Với các đa giác phức tạp hơn, việc tính diện tích các phần trở nên phức tạp và đòi hỏi nhiều kỹ thuật tính toán.

Theo nghiên cứu của Viện Toán học Việt Nam, tỷ số diện tích các phần được chia bởi đường chéo trong đa giác đều có mối liên hệ với số π và các hằng số toán học cơ bản khác.

Việc phân tích diện tích các phần này còn giúp giải quyết nhiều bài toán tối ưu, như tìm đường đi ngắn nhất qua các điểm cho trước trong đa giác.

Khi tìm hiểu về số đường chéo của đa giác, bạn sẽ khám phá được cách xác định các đường chéo và công thức tính toán chúng. Bài viết đã giới thiệu rõ ràng các phương pháp và công thức, từ việc tính số đường chéo của các đa giác đặc biệt như hình chữ nhật, hình thoi cho đến ứng dụng trong các bài toán hình học phức tạp. Việc nắm vững các kiến thức này sẽ giúp bạn tự tin hơn trong việc giải quyết bài tập toán và áp dụng vào thực tế.