Số nguyên tố là gì và những tính chất cơ bản trong toán học

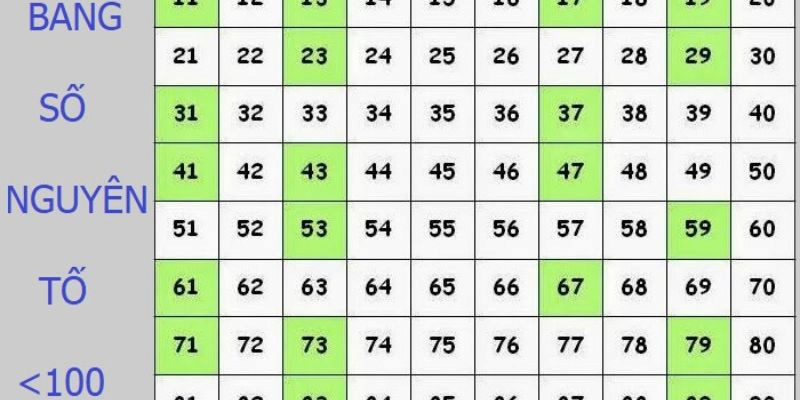
Số nguyên tố là gì? Đây là một trong những khái niệm cơ bản trong toán học mà bất kỳ ai cũng nên nắm vững. Số nguyên tố không chỉ đóng vai trò quan trọng trong lý thuyết số mà còn có ứng dụng rộng rãi trong các lĩnh vực khác nhau. Bài viết này sẽ giải thích rõ hơn về số nguyên tố, các tính chất, phương pháp tìm kiếm và bảng số nguyên tố, giúp bạn hiểu sâu hơn về chủ đề này.

Số nguyên tố là gì?

Số nguyên tố là những số nguyên dương là gì lớn hơn 1 và chỉ có đúng hai ước số là 1 và chính nó. Nói cách khác, một số nguyên tố không thể chia hết cho bất kỳ số nào khác ngoài 1 và chính nó.

Để hiểu rõ hơn về khái niệm này, ta có thể lấy ví dụ với số 7. Số 7 chỉ có hai ước số là 1 và 7, không chia hết cho 2, 3, 4, 5 hay 6. Do đó, 7 là một số nguyên tố. Ngược lại, số 6 có các ước số là 1, 2, 3 và 6 nên không phải là số nguyên tố.

Các số nguyên tố đóng vai trò quan trọng trong toán học, đặc biệt trong lý thuyết số và mật mã học. Chúng được ứng dụng rộng rãi trong bảo mật thông tin, mã hóa dữ liệu và nhiều lĩnh vực khoa học công nghệ hiện đại. Ví dụ như hệ thống mã hóa RSA, một trong những nền tảng của bảo mật internet, hoạt động dựa trên tích của hai số nguyên tố lớn.

Đặc điểm và tính chất của số nguyên tố trong toán học

Số nguyên tố là những số tự nhiên lớn hơn 1 và chỉ có đúng hai ước số dương là 1 và chính nó. Đây là một khái niệm nền tảng trong lý thuyết số học, đóng vai trò quan trọng trong việc phân tích và phân tích các mối quan hệ giữa các số.

Các số nguyên tố có tính chất đặc biệt là không thể phân tích thành tích của các số nguyên dương khác nhỏ hơn. Điều này khiến chúng trở thành “khối xây dựng” cơ bản của hệ thống số học, tương tự như nguyên tử trong hóa học.

Các tính chất cơ bản của số nguyên tố

Số nguyên tố có tính chất không thể chia hết cho bất kỳ số nào ngoài 1 và chính nó. Tính chất này làm cho việc xác định một số có phải là số nguyên tố hay không trở nên khá đơn giản về mặt lý thuyết.

Một đặc điểm quan trọng khác là không có quy luật cụ thể nào để dự đoán số nguyên tố tiếp theo trong dãy số tự nhiên. Điều này tạo nên tính phức tạp và hấp dẫn trong nghiên cứu toán học.

Mối quan hệ giữa số nguyên tố và ước số

Mối quan hệ giữa số nguyên tố và ước trong toán học là gì thể hiện rõ qua việc phân tích các số hợp số. Mỗi số hợp số đều có thể phân tích thành tích của các số nguyên tố.

Khi một số có nhiều ước số, nó chắc chắn không phải là số nguyên tố. Ngược lại, việc một số chỉ có đúng hai ước số là điều kiện đủ để xác định đó là số nguyên tố.

Số nguyên tố chỉ chia hết cho 1 và chính nó

Tính chất này là đặc trưng cơ bản nhất để nhận biết một số nguyên tố. Nó phân biệt số nguyên tố với tất cả các số hợp số khác trong hệ thống số học.

Việc kiểm tra tính chia hết này có thể thực hiện bằng cách thử chia số cần kiểm tra cho các số nhỏ hơn nó. Nếu không tìm thấy số nào chia hết ngoài 1 và chính nó, số đó là số nguyên tố.

Số nguyên tố luôn là số nguyên dương lớn hơn 1

Định nghĩa này loại trừ số 1 khỏi tập hợp số nguyên tố, mặc dù số 1 cũng chỉ có hai ước số là 1 và chính nó. Lý do là vì số 1 không đáp ứng được một số tính chất quan trọng của số nguyên tố trong các định lý toán học.

Các số âm cũng không được xem là số nguyên tố, ngay cả khi chúng chỉ có hai ước số. Điều này giúp đơn giản hóa việc nghiên cứu và ứng dụng lý thuyết số nguyên tố trong thực tế.

Phương pháp xác định và tìm số nguyên tố

Việc xác định và tìm số nguyên tố đóng vai trò quan trọng trong toán học, đặc biệt là lý thuyết số. Các phương pháp này giúp chúng ta phân tích và hiểu rõ hơn về tính chất của các số tự nhiên, tương tự như cách số e là gì đã mở ra nhiều ứng dụng trong toán học.

Để tìm được các số nguyên tố một cách hiệu quả, chúng ta cần nắm vững cả phương pháp kiểm tra từng số riêng lẻ và kỹ thuật sàng lọc hàng loạt số. Mỗi phương pháp đều có những ưu điểm và phạm vi ứng dụng riêng.

Cách kiểm tra một số có phải là số nguyên tố

Để kiểm tra một số có phải là số nguyên tố hay không, ta cần xét các ước số của nó. Một số được gọi là số nguyên tố khi chỉ có đúng hai ước số là 1 và chính nó.

Phương pháp kiểm tra cơ bản là thử chia số cần kiểm tra cho các số từ 2 đến căn bậc hai của nó. Nếu không chia hết cho số nào thì đó là số nguyên tố. Ví dụ với số 17, ta chỉ cần kiểm tra đến 4 vì √17 ≈ 4.12.

Trong thực tế, các nhà toán học thường sử dụng thuật toán Miller-Rabin để kiểm tra số nguyên tố với độ chính xác cao và tốc độ nhanh hơn nhiều so với phương pháp thông thường.

Sàng Eratosthenes – phương pháp tìm số nguyên tố hiệu quả

Sàng Eratosthenes là một trong những phương pháp hiệu quả nhất để tìm tất cả các số nguyên tố trong một khoảng cho trước. Phương pháp này được đặt theo tên của nhà toán học Hy Lạp cổ đại Eratosthenes.

Ưu điểm của phương pháp này là khả năng loại bỏ nhanh chóng các số hợp số, giúp tiết kiệm thời gian và tài nguyên tính toán đáng kể. Đặc biệt hiệu quả khi cần tìm nhiều số nguyên tố cùng lúc.

Các bước thực hiện sàng Eratosthenes

Bước đầu tiên là liệt kê tất cả các số từ 2 đến giới hạn cần tìm. Sau đó, đánh dấu số 2 là số nguyên tố và loại bỏ tất cả các bội của 2.

Tiếp theo, tìm số chưa bị đánh dấu nhỏ nhất (3), đánh dấu nó là số nguyên tố và loại bỏ các bội của nó. Quá trình này tiếp tục cho đến khi không còn số nào để xét.

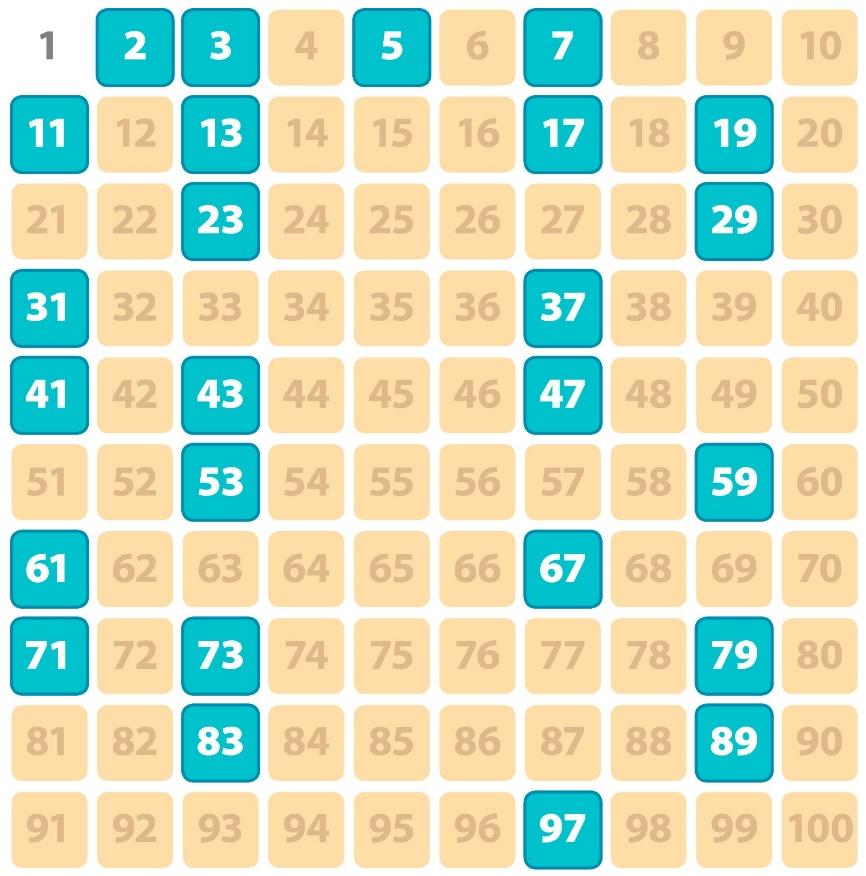
Kết quả cuối cùng, các số còn lại chưa bị đánh dấu chính là các số nguyên tố trong khoảng đã cho.

Ứng dụng trong việc lập bảng số nguyên tố

Việc lập bảng số nguyên tố có ý nghĩa quan trọng trong nghiên cứu toán học và ứng dụng thực tiễn. Các bảng này thường được sử dụng trong mã hóa, lý thuyết mật mã và nhiều lĩnh vực khác.

Sàng Eratosthenes giúp tạo ra các bảng số nguyên tố một cách nhanh chóng và chính xác. Các bảng này được lưu trữ và sử dụng trong các

Bảng các số nguyên tố từ 1 đến 100 và cách sử dụng

Bảng các số nguyên tố là công cụ quan trọng giúp tra cứu nhanh chóng các số chỉ chia hết cho 1 và chính nó. Tương tự như số phức là gì, việc nắm vững các số nguyên tố sẽ giúp giải quyết nhiều bài toán phức tạp. Để sử dụng hiệu quả, cần nắm rõ danh sách và phương pháp áp dụng phù hợp.

Danh sách các số nguyên tố từ 1 đến 100

Dãy số nguyên tố từ 1 đến 100 bao gồm: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. Các số này có đặc điểm chỉ chia hết cho 1 và chính nó, không chia hết cho bất kỳ số nào khác.

Việc ghi nhớ các số nguyên tố có thể thực hiện thông qua phương pháp phân nhóm theo hàng chục. Ví dụ nhóm 1-10 có 4 số nguyên tố là 2, 3, 5, 7; nhóm 11-20 có 4 số là 11, 13, 17, 19. Cách phân nhóm giúp dễ dàng tra cứu và áp dụng.

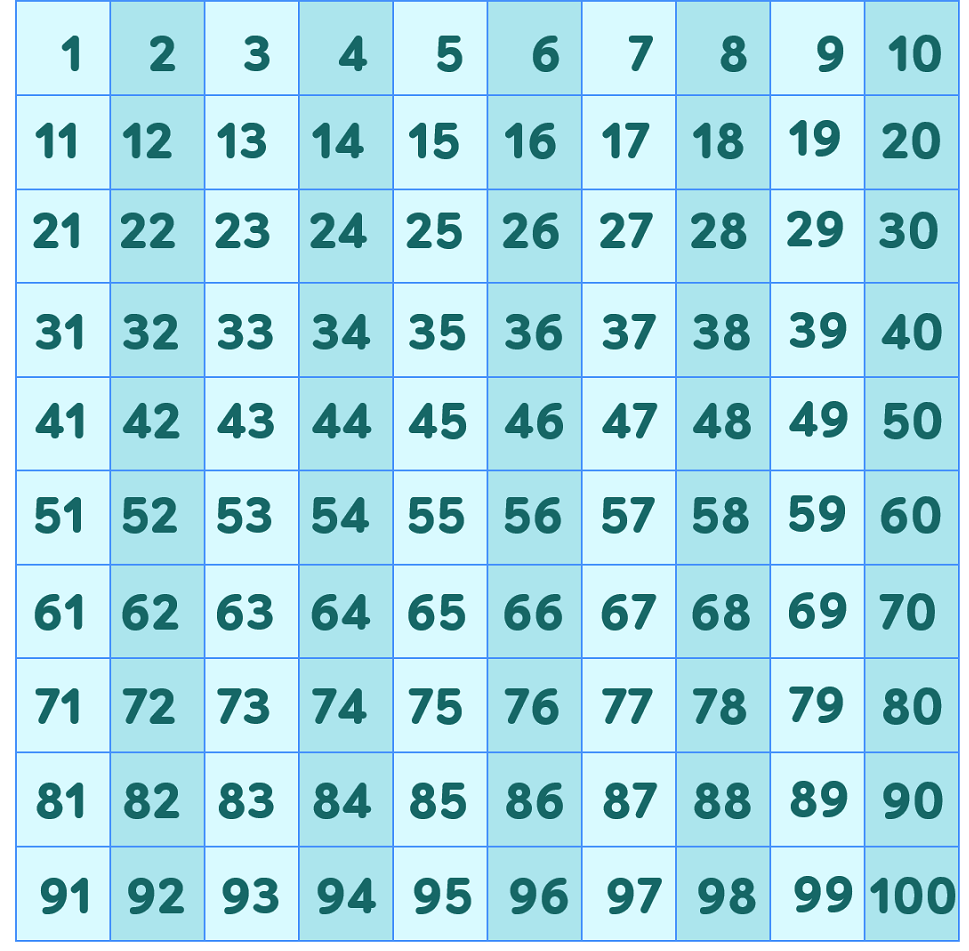
Ngoài ra, có thể sử dụng quy luật để nhận biết số nguyên tố như: số chẵn duy nhất là 2, các số còn lại đều là số lẻ và không chia hết cho các số nguyên tố nhỏ hơn nó.

Hướng dẫn sử dụng bảng số nguyên tố hiệu quả

Để sử dụng hiệu quả bảng số nguyên tố, cần nắm vững các phương pháp kiểm tra và ứng dụng. Khi cần xác định một số có phải số nguyên tố hay không, thực hiện phép chia thử với các số nguyên tố nhỏ hơn căn bậc hai của số đó.

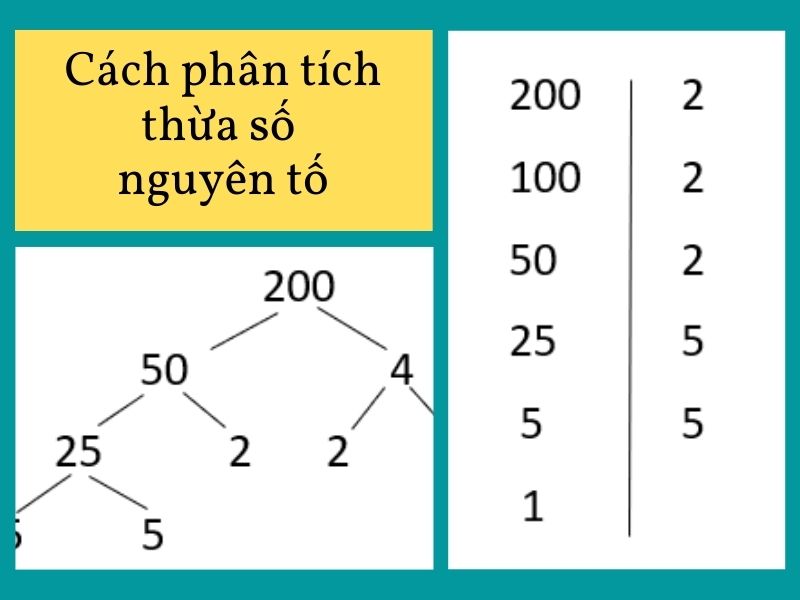
Trong phân tích thừa số nguyên tố, bảng giúp tìm nhanh các ước số nguyên tố của một số. Ví dụ số 60 = 2 x 2 x 3 x 5, trong đó 2, 3, 5 là các số nguyên tố từ bảng. Phương pháp này rất hữu ích trong các bài toán về ước số và bội số.

Ngoài ra, bảng số nguyên tố còn được ứng dụng trong mật mã học, lý thuyết số và nhiều lĩnh vực toán học nâng cao khác. Việc thành thạo sử dụng bảng sẽ giúp giải quyết nhanh chóng nhiều dạng toán phức tạp.

Những điều cần lưu ý về số nguyên tố trong toán học

Trong toán học, số nguyên tố là gì được định nghĩa là số tự nhiên lớn hơn 1 và chỉ có đúng hai ước số là 1 và chính nó. Đây là khái niệm nền tảng và có nhiều ứng dụng quan trọng trong toán học cũng như các lĩnh vực khác như mã hóa, bảo mật thông tin.

Để hiểu rõ hơn về số nguyên tố, có một số đặc điểm quan trọng cần nắm vững. Đặc biệt là các trường hợp đặc biệt như số 1 hay số 2 thường gây nhầm lẫn cho nhiều người. Ngoài ra, việc tìm hiểu về 0 có phải số nguyên dương không cũng giúp phân biệt rõ ràng hơn các khái niệm cơ bản trong toán học.

Số 1 không phải là số nguyên tố

1 có phải số nguyên tố không là câu hỏi thường gặp. Câu trả lời là không – số 1 không được coi là số nguyên tố. Lý do chính là vì số 1 chỉ có một ước số duy nhất là chính nó, không thỏa mãn định nghĩa về số nguyên tố cần có đúng hai ước số.

Việc loại số 1 ra khỏi tập hợp số nguyên tố có ý nghĩa quan trọng trong việc bảo toàn các tính chất của số nguyên tố. Nếu coi 1 là số nguyên tố, nhiều định lý quan trọng về phân tích thừa số nguyên tố sẽ không còn đúng.

Số 2 là số nguyên tố nhỏ nhất và duy nhất là số chẵn

Số nguyên tố nhỏ nhất là 2 – đây là một trường hợp đặc biệt vì nó vừa là số nguyên tố vừa là số chẵn. Số 2 có đúng hai ước số là 1 và 2, thỏa mãn định nghĩa của số nguyên tố.

Tất cả các số nguyên tố lớn hơn 2 đều là số lẻ, vì mọi số chẵn lớn hơn 2 đều chia hết cho 2 nên có ít nhất 3 ước số. Điều này làm cho số 2 trở thành số nguyên tố chẵn duy nhất, một tính chất độc đáo trong lý thuyết số.

Tầm quan trọng của số nguyên tố trong toán học

Số nguyên tố đóng vai trò then chốt trong nhiều lĩnh vực của toán học. Chúng là nền tảng cho định lý cơ bản về số học, theo đó mọi số tự nhiên lớn hơn 1 đều có thể phân tích thành tích của các số nguyên tố.

Trong thực tế, số nguyên tố được ứng dụng rộng rãi trong mã hóa RSA – một hệ thống bảo mật được sử dụng phổ biến trên Học Thế Nào và nhiều nền tảng khác. Việc tìm kiếm số nguyên tố lớn cũng là một lĩnh vực nghiên cứu quan trọng trong toán học hiện đại.

Các nhà toán học vẫn tiếp tục nghiên cứu về tính chất và phân bố của số nguyên tố, với nhiều bài toán nổi tiếng vẫn chưa được giải quyết như giả thuyết Goldbach hay giả thuyết số nguyên tố sinh đôi.

Khi tìm hiểu về số nguyên tố là gì, bạn sẽ thấy đây là một khái niệm cơ bản nhưng vô cùng quan trọng trong toán học. Số nguyên tố chỉ chia hết cho 1 và chính nó, và số 2 là số nguyên tố nhỏ nhất. Hiểu rõ đặc điểm và cách tìm số nguyên tố sẽ giúp bạn có nền tảng vững chắc trong việc khám phá các lĩnh vực toán học tiếp theo.