Thể tích hình bát diện đều là kiến thức cơ bản trong chương giáo dục THPT tại Việt Nam. Nó đóng vai trò quan trọng trong nhiều lĩnh vực như toán học, vật lý… và ngày nay được ứng dụng rất nhiều trong đời sống hằng ngày. Bài viết dưới đây, chúng tôi sẽ cung cấp cho bạn đầy đủ kiến thức về nội dung này.
Thể tích hình bát diện đều là gì?
Thể tích của hình bát diện đều được định nghĩa là lượng không gian bên trong hình bát diện đều và được tính bằng đơn vị khối lượng như mét khối (m³) hoặc centimét khối (cm³).
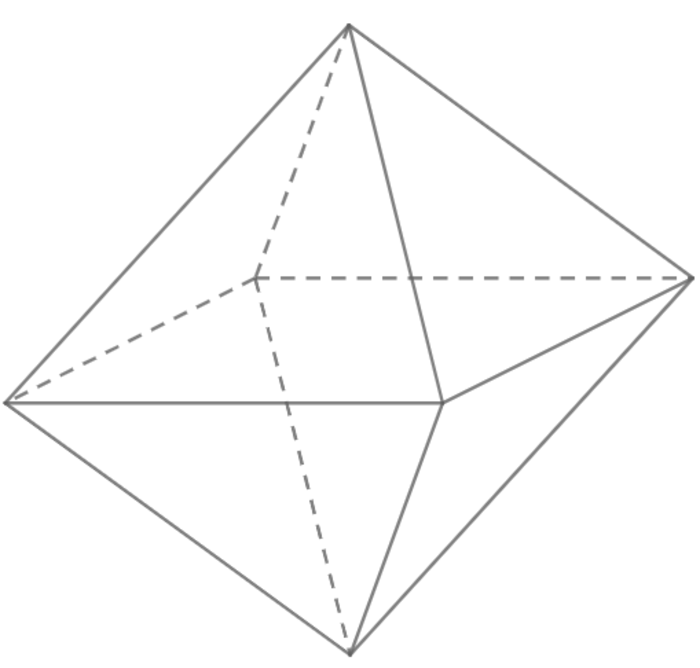
Công thức tính thể tích của hình bát diện đều là V = (√2/3)a³
Trong đó: a là độ dài cạnh của hình.
Công thức này thể hiện mối quan hệ giữa kích thước cạnh và không gian nội tại của hình, phản ánh đặc tính hình học độc đáo của bát diện đều. Thể tích này có ý nghĩa quan trọng trong nhiều ứng dụng thực tế, từ thiết kế và sản xuất đến nghiên cứu khoa học, cho phép tính toán chính xác lượng vật chất hoặc dung tích mà hình bát diện đều có thể chứa đựng.
Các công thức tính thể tích hình bát diện đều
Bên cạnh công thức căn bản được cung cấp phía trên, chúng ta có thể tính thể tích hình bát diện đều qua các công thức sau:
Theo bán kính đường tròn ngoại tiếp
Công thức: V = (4/3)√2R³
Trong đó: R là bán kính đường tròn ngoại tiếp.
Công thức này liên hệ thể tích với bán kính đường tròn ngoại tiếp. Nó đặc biệt hữu ích khi hình bát diện đều được mô tả trong mối quan hệ với hình cầu bao quanh nó, thường gặp trong các bài toán thiên văn học hoặc thiết kế quang học.
Theo bán kính đường tròn nội tiếp
Công thức: V = 8√2r³
Trong đó: r là bán kính đường tròn nội tiếp.

Sử dụng bán kính đường tròn nội tiếp, công thức này có ứng dụng trong các tình huống liên quan đến không gian bên trong của hình bát diện đều.
Theo diện tích toàn phần
Công thức: V = (√2/12)S√S
Trong đó: S là diện tích toàn phần.
Công thức này thể hiện mối quan hệ giữa thể tích và diện tích toàn phần. Nó hữu ích trong các bài toán liên quan đến bề mặt và thể tích.Ví dụ nó được sử dụng trong nghiên cứu về tỷ lệ diện tích/thể tích trong sinh học hoặc vật liệu học.
Theo tổng độ dài cạnh
Công thức: V = (L³)/(1728√2)
Trong đó: L là tổng độ dài các cạnh.
Liên hệ thể tích với tổng độ dài cạnh, công thức này có thể hữu ích trong các tình huống khi tổng độ dài cạnh là thông số dễ đo lường hơn các thông số khác. Ví dụ như trong một số ứng dụng sản xuất hoặc thiết kế.
Liên hệ với thể tích hình lập phương ngoại tiếp
Công thức: V = (1/3)Vcube
Trong đó Vcube là thể tích hình lập phương ngoại tiếp. Công thức này thể hiện mối quan hệ giữa thể tích hình bát diện đều và hình lập phương bao quanh nó. Nó đặc biệt hữu ích trong các bài toán so sánh hình học hoặc tối ưu hóa không gian.
Ví dụ minh họa
Những ví dụ minh họa sau đây sẽ giúp bạn hiểu rõ hơn thể tích hình bát diện đều là gì.
Ví dụ cơ bản
Đề bài: Một hình bát diện đều có cạnh dài 6 cm. Tính thể tích của hình này.
Lời giải:
Ta có công thức: V = (√2/3)a³
Trong đó: V là thể tích, a là độ dài cạnh
Thay số: a = 6 cm
Tính toán:
V = (√2/3) × 6³
= (√2/3) × 216
= 72√2
≈ 101.823 cm³
Vậy thể tích của hình bát diện đều là 72√2 cm³ hoặc xấp xỉ 101.823 cm³.
Ví dụ nâng cao
Đề bài: Một hình bát diện đều có diện tích toàn phần là 144√3 cm². Tính thể tích của hình này.
Lời giải:
Ta có công thức: V = (√2/12)S√S
Trong đó: V là thể tích, S là diện tích toàn phần
Thay số: S = 144√3 cm²
Tính toán:
V = (√2/12) × 144√3 × √(144√3)
= (√2/12) × 144√3 × 12√3
= (√2/12) × 1728 × 3
= √2 × 144 × 3
= 432√2
≈ 610.94 cm³
Vậy thể tích của khối bát diện đều là 432√2 cm³ hoặc xấp xỉ 610.94 cm³.
Ứng dụng thực tiễn của thể tích hình bát diện đều
Thể tích khối đa diện tám mặt không chỉ được sử dụng trong giáo dục. Trong các lĩnh vực khác nhau nó lại có những ứng dụng quan trọng khác nhau.
Trong lĩnh vực tinh thể học và khoa học vật liệu
Trong lĩnh vực tinh thể học và khoa học vật liệu, thể tích khối đa diện tám mặt đều đóng vai trò quan trọng trong việc nghiên cứu cấu trúc tinh thể. Nhiều kim loại và hợp chất có cấu trúc tinh thể dạng bát diện đều ở cấp độ nguyên tử.
Các nhà khoa học sử dụng công thức thể tích để tính toán mật độ nguyên tử, dự đoán tính chất vật liệu, và thiết kế vật liệu mới với đặc tính mong muốn. Ví dụ, trong nghiên cứu về siêu dẫn hoặc vật liệu từ tính, hiểu biết về thể tích của cấu trúc bát diện đều giúp giải thích và dự đoán các tính chất quan trọng của vật liệu.
Trong ngành công nghiệp dược phẩm và hóa chất
Trong ngành công nghiệp dược phẩm và hóa chất, thể tích khối đa diện tám mặt đều được ứng dụng trong thiết kế và sản xuất các phân tử phức tạp.
Nhiều hợp chất hóa học có cấu trúc phân tử dạng bát diện, và việc tính toán chính xác thể tích của chúng là cần thiết để hiểu rõ về tương tác giữa các phân tử, khả năng liên kết, và hoạt tính sinh học. Trong phát triển thuốc mới, thông tin về thể tích phân tử giúp dự đoán khả năng thâm nhập qua màng tế bào và tương tác với các thụ thể, từ đó tối ưu hóa hiệu quả của thuốc.
Trong ngành công nghệ nano
Trong ngành công nghệ nano, thể tích khối đa diện tám mặt đều được sử dụng trong thiết kế và sản xuất các cấu trúc nano. Các nhà khoa học tạo ra các hạt nano có hình dạng bát diện đều để ứng dụng trong nhiều lĩnh vực như xúc tác, lọc nước, và phân phối thuốc.

Việc kiểm soát chính xác thể tích của các hạt nano này là cực kỳ quan trọng để đạt được hiệu suất mong muốn trong các ứng dụng . Cụ thể, như tối ưu hóa diện tích bề mặt cho phản ứng xúc tác hoặc điều chỉnh khả năng giải phóng thuốc trong cơ thể.
Lời kết
Có thể thấy, thể tích hình bát diện đều không chỉ là kiến thức được sử dụng trong chương trình giáo dục. Nội dung này đóng vai trò vô cùng quan trọng trong sự phát triển của nhiều lĩnh vực khoa học kỹ thuật, hay đời sống hằng ngày.




