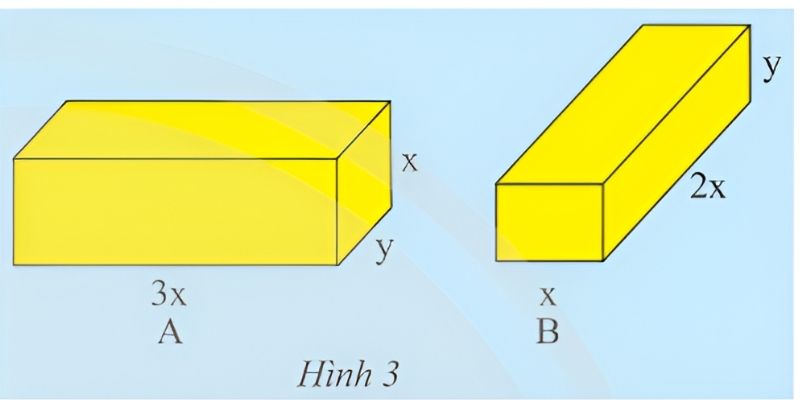
Thể tích hình hộp chữ nhật là gì? Thể tích là một khái niệm quan trọng và được sử sống.dụng rất nhiều trong cuộc sống hàng ngày. Nó liên quan đến không gian và kích thước của các hình dạng khác nhau, giúp chúng ta có thể tính toán lượng không gian mà một vật chiếm giữ.
Công thức tính Thể tích Hình hộp chữ nhật
Hình hộp chữ nhật là một hình khối ba chiều được giới hạn bởi sáu mặt hình chữ nhật, trong đó các mặt đối diện song song và bằng nhau. Thể tích của hình hộp chữ nhật là lượng không gian mà hình hộp đó chiếm giữ trong không gian ba chiều. Để tính được thể tích của khối hộp chữ nhật, chúng ta cần biết các yếu tố cấu tạo nên hình hộp đó, bao gồm:
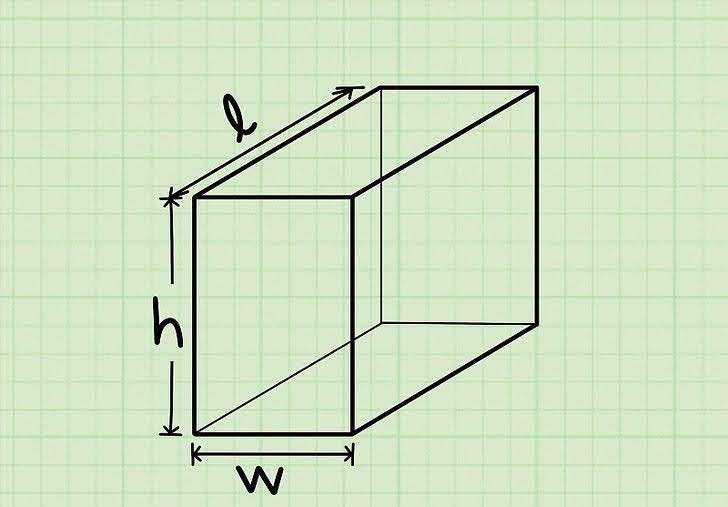
- Chiều dài (d): Độ dài của một cạnh đáy của hình hộp chữ nhật.
- Chiều rộng (r): Độ dài của cạnh đáy còn lại của hình hộp chữ nhật.
- Chiều cao (h): Khoảng cách vuông góc giữa hai mặt đáy của hình hộp chữ nhật.
Theo đó, công thức tính thể tích khối hộp chữ nhật được tính bằng cách nhân chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật:
$$V=d\times r\times h$$
Trong đó:
- V: Thể tích khối hộp chữ nhật
- d: Chiều dài hình hộp chữ nhật
- r: Chiều rộng hình hộp chữ nhật
- h: Chiều cao hình hộp chữ nhật
Lưu ý: Thể tích được đo bằng đơn vị khối, ví dụ như cm³, m³, dm³,… Nếu các cạnh của hình hộp chữ nhật được đo bằng cùng một đơn vị đo, thì thể tích của hình hộp sẽ có đơn vị đo tương ứng với đơn vị đo của các cạnh.
Xem thêm: Công thức tính diện tích hình hộp chữ nhật chính xác
Ứng dụng của công thức tính Thể tích khối hộp chữ nhật
Công thức tính thể tích khối hộp chữ nhật được ứng dụng rất rộng rãi trong cuộc sống và trong các lĩnh vực như:
Xây dựng
Trong ngành xây dựng, tính toán thể tích khối hộp chữ nhật là rất quan trọng và cần thiết trong việc xác định khối lượng vật liệu cần thiết để xây dựng một công trình. Việc tính toán chính xác thể tích giúp người thợ xây có thể tính toán số lượng bê tông, cát, sỏi, gạch,… cần thiết để xây dựng các công trình như nhà cửa, nền móng, tường rào,…
Khoa học
Trong lĩnh vực khoa học, tính toán thể tích của các vật thể có hình dạng hộp chữ nhật là rất cần thiết. Ví dụ, trong nghiên cứu vật lý, các nhà khoa học cần tính toán thể tích của các vật thể để đo lường khối lượng và nghiên cứu các tính chất của chúng. Việc tính toán thể tích cũng được áp dụng trong lĩnh vực hóa học, sinh học và các lĩnh vực khác.
Phân biệt thể tích hình hộp chữ nhật và hình lập phương
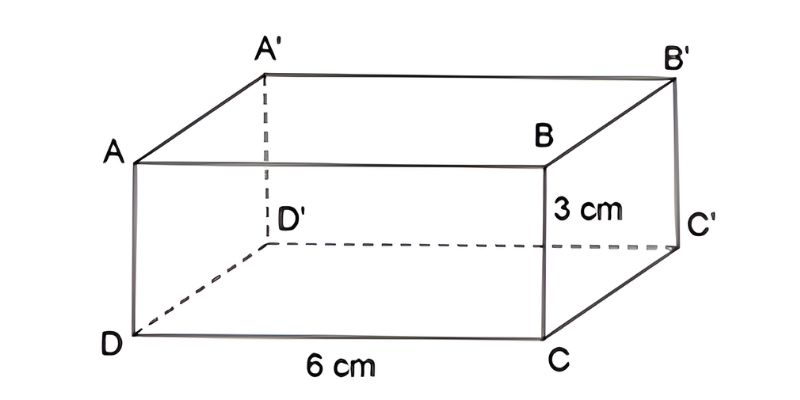Thể tích khối hộp chữ nhật
- Để tính thể tích khối hộp chữ nhật, ta nhân chiều dài, chiều rộng và chiều cao của hình hộp với nhau theo công thức V = d x r x h.
- Thể tích khối hộp chữ nhật được đo bằng đơn vị khối (cm³, m³, etc.).
- Hình hộp chữ nhật có diện tích mặt đáy là d x r.
Thể tích khối lập phương
- Đối với hình lập phương, ta chỉ cần nhân độ dài cạnh của hình vuông với chính nó 3 lần, tức là V = a x a x a = a³.
- Thể tích hình lập phương cũng được đo bằng đơn vị khối (cm³, m³, etc.).
- Hình lập phương không có chiều dài, chiều rộng, chỉ có cạnh.
Khi phân biệt giữa thể tích của khối hộp chữ nhật và hình lập phương, chúng ta cần lưu ý về số chiều và cách tính thể tích của từng loại hình để không nhầm lẫn trong quá trình tính toán.
Bài tập ví dụ về tính Thể tích khối hộp chữ nhật
Để hiểu rõ hơn về cách tính thể tích khối hộp chữ nhật, chúng ta cùng xem qua một vài bài tập ví dụ sau đây:
Bài tập 1: Một thùng chứa nước có hình dạng hình hộp chữ nhật, chiều dài là 20cm, chiều rộng là 15cm và chiều cao là 10cm. Hỏi thể tích của thùng nước này là bao nhiêu?
Giải: Đầu tiên, ta cần tìm diện tích mặt đáy A của thùng nước, theo công thức $$A=d\times r=20cm\times15cm=300cm²$$. Sau đó, áp dụng công thức $$V=A\times h=300cm²x10cm=3000cm³$$. Vậy thể tích của thùng nước là 3000cm³.
Bài tập 2: Một chiếc hộp hàng có hình dạng hình hộp chữ nhật, chiều dài là 40cm, chiều rộng là 30cm và chiều cao là 25cm. Giả sử chiếc hộp này chứa đầy các sản phẩm, hỏi thể tích tối đa của chiếc hộp là bao nhiêu?
Giải: Tương tự như bài tập 1, ta cần tìm diện tích mặt đáy A của chiếc hộp, theo công thức $$A=d\times r=40cm\times30cm=1200cm²$$. Sau đó, áp dụng công thức $$V=A\times h=1200cm²x25cm=30000cm³$$. Vậy thể tích tối đa của chiếc hộp là 30000cm³.
Kết luận
Như vậy, qua bài viết này chúng ta đã cùng tìm hiểu về khái niệm về thể tích khối hộp chữ nhật, cách tính và ứng dụng của công thức tính thể tích này. Chúng ta cũng đã phân biệt sự khác nhau giữa thể tích của khối hộp chữ nhật và hình lập phương. Việc hiểu và áp dụng công thức tính thể tích hình hộp chữ nhật là rất quan trọng trong việc giải quyết các bài toán liên quan đến không gian ba chiều và thực tế.
