Thể tích khối cầu là một trong những kiến thức căn bản đối với chương trình THPT tại Việt Nam. Nó đóng vai trò vô cùng quan trọng trong nhiều lĩnh vực như: Toán học, vật lý, kỹ thuật cho đến cuộc sống hàng ngày của chúng ta. Bài viết dưới đây của Hocthenao sẽ giúp bạn tìm ra công thức tính thể tích, các bước giải và ứng dụng của khối cầu trong thực tế.
Khái niệm và công thức tính thể tích khối cầu
Thể tích khối cầu là đại lượng đo lường không gian mà khối cầu đó chiếm giữ trong không gian ba chiều. Nó được tính bằng lượng chất lỏng cần thiết để đổ đầy khối cầu đó.
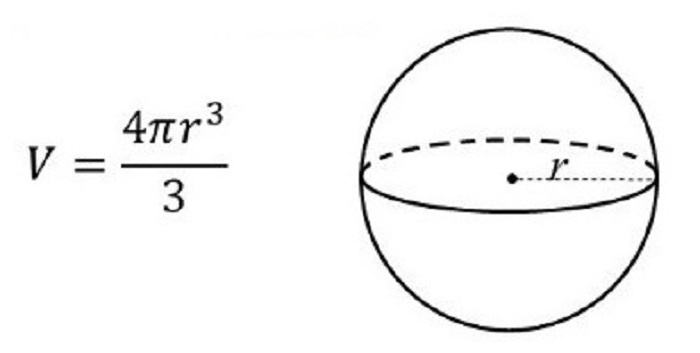
Công thức tính thể tích khối cầu có dạng đầy đủ như sau:
$$ V=\frac43\mathrm{πR}^3 $$
Trong đó:
- V là thể tích khối cầu (đơn vị mét khối, m³)
- π là hằng số Pi, xấp xỉ bằng 3,14
- r là bán kính khối cầu (đơn vị mét, m)
Ví dụ minh hoạ:
Một quả bóng đá có bán kính 10 cm. Tính thể tích của quả bóng đá đó.
Giải:
Ta có bán kính r = 10 cm.
Thay r vào công thức: V = (4/3)π(10³) = (4/3)π * 1000 = 4188,79 cm³.
Ứng dụng của thể tích hình cầu trong thực tế
Việc tính toán thể tích hình cầu có rất nhiều ứng dụng quan trọng trong nhiều lĩnh vực khác nhau. Chẳng hạn như:
- Xây dựng: Tính toán lượng vật liệu cần thiết cho các công trình hình cầu như mái vòm, bể chứa nước,…
- Khoa học kỹ thuật: Thể tích hình cầu được sử dụng trong nhiều lĩnh vực khoa học kỹ thuật như chế tạo máy móc, thiết bị, nghiên cứu khoa học,…
- Đời sống hàng ngày: Ttính toán dung tích của các vật dụng hình cầu như bình gas, quả bóng, nồi cơm điện,…
Mối liên hệ giữa thể tích khối cầu và các hình học khác
Công thức tính thể tích hình cầu có mối liên hệ chặt chẽ với thể tích của một số hình học khác, bao gồm:
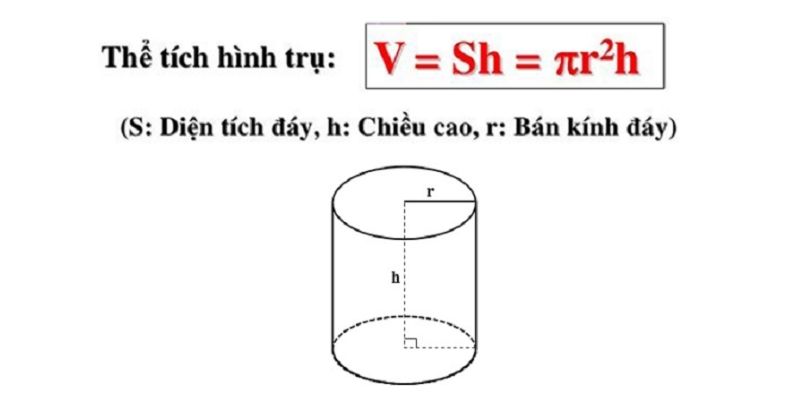
- Khối trụ:
Thể tích khối cầu bằng 2/3 thể tích khối trụ có cùng bán kính đáy và chiều cao. Công thức:
Vcầu = (2/3) * Vtrụ
- Hình nón:
Thể tích khối cầu bằng 1/3 thể tích hình nón có cùng bán kính đáy và chiều cao. Công thức:
Vcầu = (1/3) * Vnón
- Hình chóp tứ giác đều:
Thể tích khối cầu bằng 1/6 thể tích hình chóp tứ giác đều có cạnh đáy và chiều cao bằng nhau. Công thức:
Vcầu = (1/6) * Vchóp
Mối liên hệ này xuất phát từ việc khối cầu, khối trụ, hình nón và hình chóp tứ giác đều có thể được chia thành nhiều phần nhỏ có hình dạng giống nhau. Ví dụ, khối cầu có thể được chia thành nhiều khối trụ nhỏ, hình nón có thể được chia thành nhiều khối cầu nhỏ, và hình chóp tứ giác đều có thể được chia thành nhiều khối nón nhỏ. Do đó, thể tích của khối cầu có thể được tính toán bằng cách tính tổng thể tích của các phần nhỏ này.
Ví dụ:
Giả sử ta có một khối cầu, một khối trụ và một hình nón có cùng bán kính đáy R và chiều cao H.
- Thể tích khối cầu: Vcầu = (4/3)πR³
- Thể tích khối trụ: Vtrụ = πR²H
- Thể tích hình nón: Vnón = (1/3)πR²H
Theo công thức trên, ta có:
Vcầu = (2/3) * Vtrụ = (2/3) * πR²H
Vcầu = (1/3) * Vnón = (1/3) * (1/3)πR²H = (1/9)πR²H
Các bước giải bài tập tính thể tích khối cầu
Để giải bài tập tính thể tích hình cầu một cách chính xác và hiệu quả, bạn cần thực hiện theo các bước sau:
Bước 1: Phân tích đề bài
Đây là bước đơn giản nhất nhưng cũng vô cùng quan trọng:
- Xác định các thông tin được cho trong đề bài, bao gồm: bán kính khối cầu, đường kính khối cầu, diện tích mặt cầu,…
- Xác định yêu cầu của đề bài: tính thể tích khối cầu.
Bước 2: Chọn công thức tính phù hợp
Dựa vào thông tin đã phân tích ở bước 1, bạn cần chọn công thức tính thể tích phù hợp. Có hai công thức chính được sử dụng:
Công thức tính theo bán kính:
$$ V=\frac43\mathrm{πR}^3 $$
Trong đó:
- V là thể tích khối cầu (đơn vị mét khối, m³)
- π là hằng số Pi, xấp xỉ bằng 3,14
- r là bán kính khối cầu (đơn vị mét, m)
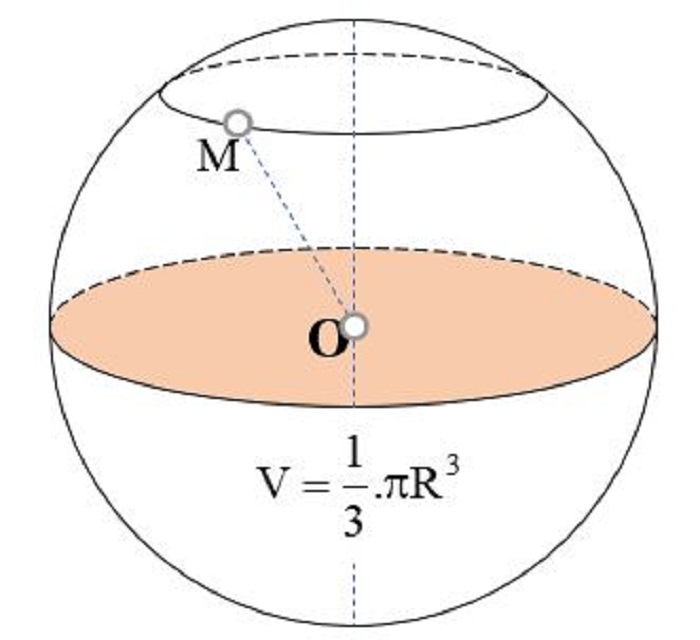
Công thức tính theo đường kính:
$$ V=\frac43\mathrm\pi{(\frac{\mathrm d}2)}^3 $$
Trong đó:
- V là thể tích khối cầu (đơn vị mét khối, m³)
- π là hằng số Pi, xấp xỉ bằng 3,14
- d là đường kính khối cầu (đơn vị mét, m)
Bước 3: Thay giá trị vào công thức và tính toán
Tiếp theo, ta thực hiện các thao tác:
- Thay giá trị bán kính hoặc đường kính khối cầu đã được xác định ở bước 1 vào công thức tính thể tích đã chọn ở bước 2.
- Thực hiện phép tính để tìm ra thể tích hình đã cho.
Bước 4: Kiểm tra kết quả
Bước cuối cùng trong cách giải đó là kiểm tra kết quả:
- Sau khi tính toán, bạn cần kiểm tra lại kết quả xem có hợp lý hay không.
- Có thể so sánh kết quả với các ví dụ tương tự hoặc sử dụng các phương pháp kiểm tra khác.
Bài tập có lời giải về tính thể tính khối trụ
Để giúp bạn luyện tập và củng cố kiến thức về thể tích khối cầu, chúng tôi đã tổng hợp một số bài tập có lời giải chi tiết mà bạn có thể tham khảo:
Bài tập 1
Một quả cầu có đường kính 12 cm. Tính thể tích của quả cầu.
Giải:
- Bán kính r = đường kính d/2 = 12 cm/2 = 6 cm.
- Áp dụng công thức tính thể tích:
V = (4/3)πr³ = (4/3)π(6³) = (4/3)π * 216 = 576π cm³.
Kết quả: Thể tích của quả cầu là 576π cm³.
Bài tập 2
Một bể nước hình cầu có bán kính 1,5 mét. Tính thể tích của bể nước.
Giải:
- Áp dụng công thức tính thể tích hình cầu:
V = (4/3)πr³ = (4/3)π(1,5³) = (4/3)π * 3,375 = 14,137π m³.
Kết quả: Thể tích của bể nước là 14,137π m³.
Bài tập 3
Một khối kim loại có hình dạng khối cầu với bán kính 3 cm. Khối kim loại đó được nung chảy và đúc thành một hình trụ có chiều cao 5 cm. Tính bán kính đáy của hình trụ.
Giải:
- Gọi bán kính đáy của hình trụ là x cm.
- Thể tích khối kim loại không thay đổi sau khi nung chảy và đúc thành hình trụ.
- Do đó, ta có phương trình:
(4/3)π(3³) = πx² * 5
Giải phương trình, ta được:
x² = (4/3) * 3² = 12
x = √12 = 2√3 cm.
Kết quả: Bán kính đáy của hình trụ là 2√3 cm.
Bài tập 4
Một hình chóp tứ giác đều có cạnh đáy là 8 cm và chiều cao là 10 cm. Tính thể tích của phần khối cầu nội tiếp hình chóp.
Giải:
Bán kính đáy của hình chóp tứ giác đều là a/√2, với a là cạnh đáy.
Do đó, bán kính đáy của hình chóp tứ giác đều trong bài toán này là 8 cm/√2 = 4√2 cm.
Chiều cao của hình chóp tứ giác đều cũng là bán kính của phần khối cầu nội tiếp.
- Áp dụng công thức tính thể tích:
V = (4/3)π(4√2³) = (4/3)π * 256√2 = 342,07π cm³.
Kết quả: Thể tích của phần khối cầu nội tiếp hình chóp là 342,07π cm³.
Bài tập 5
Một hình nón có bán kính đáy là 6 cm và chiều cao là 8 cm. Tính thể tích của phần khối cầu nội tiếp hình nón.
Giải:
- Bán kính đáy của hình nón cũng là bán kính của phần khối cầu nội tiếp.
- Áp dụng công thức tính thể tích:
V = (4/3)π(6³) = (4/3)π * 216 = 576π cm³.
Kết quả: Thể tích của phần khối cầu nội tiếp hình nón là 576π cm³.
Lời kết
Thể tích khối cầu là một khái niệm quan trọng trong toán học và có nhiều ứng dụng quan trọng trong thực tế. Nắm rõ công thức tính toán và cách áp dụng sẽ giúp bạn giải quyết các bài toán hình học liên quan đến chủ đề này một cách nhanh chóng và hiệu quả.
Bài viết liên quan
