Trung điểm là gì? Khái niệm, công thức và ứng dụng trong hình học

Trung điểm là gì? Đây là một khái niệm quan trọng trong hình học, đặc biệt là khi làm việc với đoạn thẳng. Bài viết này sẽ trình bày các kiến thức cơ bản, tính chất và cách xác định trung điểm. Thêm vào đó, bạn cũng sẽ tìm thấy các ứng dụng và ví dụ minh họa giúp bạn hiểu rõ hơn về vấn đề này.

Trung điểm là gì?

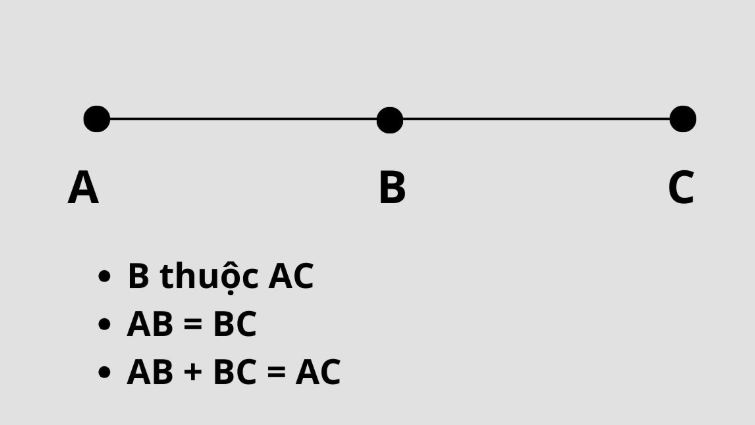
Trung điểm là điểm nằm chính giữa của một đoạn thẳng, chia đoạn thẳng đó thành hai phần bằng nhau. Nói cách khác, khoảng cách từ trung điểm đến hai đầu mút của đoạn thẳng luôn bằng nhau.

Trong hình học phẳng, trung điểm đóng vai trò quan trọng trong việc xác định vị trí và tính toán các yếu tố hình học. Ví dụ, trung điểm của đường chéo trong hình chữ nhật là giao điểm của hai đường chéo, và cũng là tâm đối xứng của hình chữ nhật.

Về mặt tọa độ, trung điểm M của đoạn thẳng AB có tọa độ được tính bằng công thức: xM = (xA + xB)/2 và yM = (yA + yB)/2, trong đó (xA,yA) và (xB,yB) lần lượt là tọa độ của điểm A và điểm B. Công thức này giúp xác định chính xác vị trí của trung điểm trên mặt phẳng tọa độ.

Khái niệm và tính chất cơ bản của trung điểm trong hình học

Trung điểm là điểm nằm chính giữa một đoạn thẳng, chia đoạn thẳng đó thành hai phần bằng nhau. Trong hình học, trung điểm đóng vai trò quan trọng khi nghiên cứu các tính chất của hình học phẳng và không gian, tương tự như điểm uốn là gì trong đồ thị hàm số.

Về mặt tọa độ, trung điểm của đoạn thẳng AB có tọa độ là trung bình cộng của tọa độ hai điểm đầu mút. Điều này có nghĩa nếu A(x1,y1) và B(x2,y2) thì trung điểm M sẽ có tọa độ M((x1+x2)/2, (y1+y2)/2). Đây là một trong những tính chất trung điểm cơ bản nhất được ứng dụng rộng rãi.

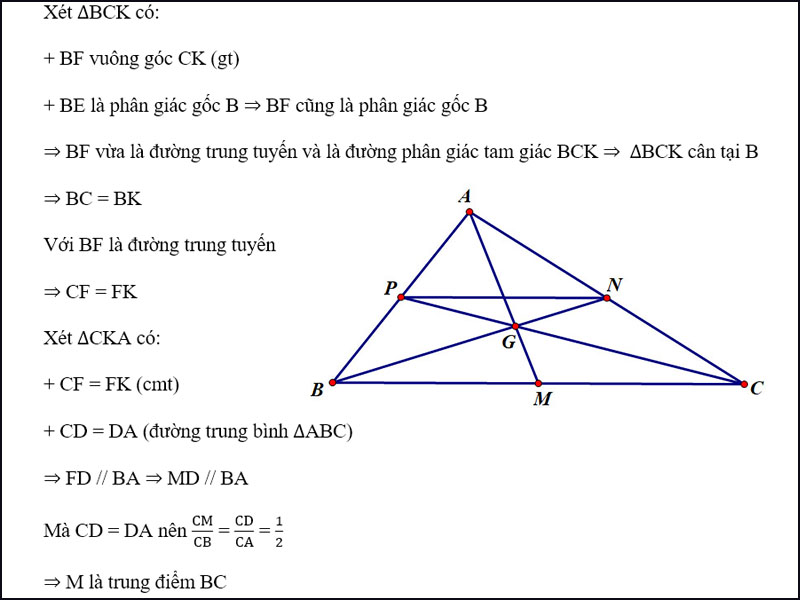
Trong tam giác, trung điểm của các cạnh có mối liên hệ đặc biệt với trọng tâm. Khi nối trung điểm của hai cạnh bất kỳ, ta được một đoạn thẳng song song với cạnh còn lại và có độ dài bằng một nửa cạnh đó. Tính chất này thường được gọi là định lý trung điểm và có nhiều ứng dụng trong việc giải các bài toán hình học phức tạp.

Ngoài ra, trung điểm còn là yếu tố then chốt trong nhiều phép biến hình như phép vị tự, phép đối xứng tâm. Khi áp dụng phép đối xứng qua một điểm, điểm đó chính là trung điểm của đoạn thẳng nối một điểm bất kỳ với ảnh của nó qua phép đối xứng. Điều này cho thấy vai trò quan trọng của trung điểm trong việc xác định và nghiên cứu các phép biến hình hình học.

Cách xác định trung điểm của đoạn thẳng trong toán học

Trung điểm của đoạn thẳng là điểm nằm chính giữa và chia đoạn thẳng thành hai phần bằng nhau. Việc xác định trung điểm có vai trò quan trọng trong nhiều bài toán hình học và ứng dụng thực tế như thiết kế, xây dựng.

Để xác định chính xác trung điểm, có thể sử dụng phương pháp đo đạc thủ công hoặc áp dụng công thức toán học. Mỗi phương pháp đều có những ưu điểm riêng tùy theo mục đích sử dụng và độ chính xác cần thiết.

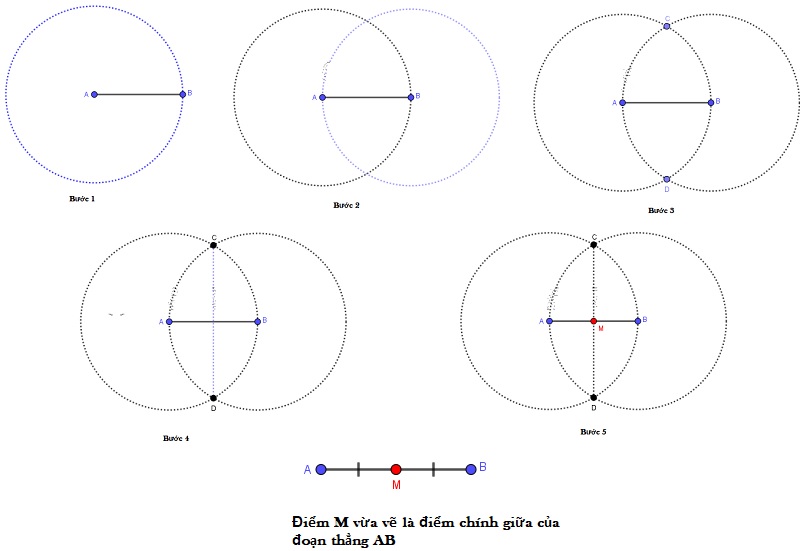
Phương pháp tìm trung điểm bằng thước kẻ và compa

Cách tìm trung điểm bằng thước kẻ và compa là phương pháp cơ bản nhất. Đầu tiên, dùng compa vẽ hai cung tròn bán kính bằng nhau tại hai đầu đoạn thẳng. Sau đó, nối hai giao điểm của hai cung tròn để tạo thành đường thẳng vuông góc với đoạn thẳng ban đầu.

Điểm giao của hai đường thẳng chính là trung điểm cần tìm. Phương pháp này thường được sử dụng trong các bài toán hình học cơ bản và giúp học sinh hiểu rõ bản chất của trung điểm là điểm cách đều hai đầu mút.

Công thức tính tọa độ trung điểm

Để tính toán chính xác tọa độ trung điểm, trung vị là gì và các khái niệm thống kê khác cần được nắm vững. Công thức tính tọa độ trung điểm được chia thành hai trường hợp chính:

Trường hợp trên trục tọa độ

Khi đoạn thẳng nằm trên trục hoành hoặc trục tung, tọa độ trung điểm được xác định bằng cách lấy trung bình cộng của hai tọa độ tương ứng. Nếu đoạn thẳng nằm trên trục Ox, tọa độ y không thay đổi. Ngược lại, với đoạn thẳng trên trục Oy, tọa độ x giữ nguyên.

Việc tính toán trong trường hợp này khá đơn giản vì chỉ cần xử lý một tọa độ duy nhất. Tuy nhiên, cần chú ý đến dấu của các số để tránh sai sót không đáng có.

Trường hợp trong mặt phẳng tọa độ

Khi đoạn thẳng nằm trong mặt phẳng tọa độ, tọa độ trung điểm M(x,y) của đoạn thẳng AB với A(x₁,y₁) và B(x₂,y₂) được tính theo công thức: x = (x₁ + x₂)/2 và y = (y₁ + y₂)/2.

Phương pháp này áp dụng cho mọi vị trí của đoạn thẳng trong mặt phẳng tọa độ. Việc nắm vững công thức và thực hành nhiều bài tập sẽ giúp giải quyết nhanh chóng các bài toán liên quan đến công thức trung điểm.

Đường trung điểm và ứng dụng trong tam giác

Đường trung điểm trong tam giác là một khái niệm hình học quan trọng, giúp giải quyết nhiều bài toán phức tạp. Việc nắm vững các tính chất và ứng dụng của đường trung điểm sẽ giúp học sinh tiếp cận các bài toán hình học một cách hiệu quả hơn.

Khái niệm đường trung điểm trong tam giác

Trong tam giác ABC, đường thẳng nối một đỉnh với trung điểm của cạnh đối diện được gọi là trung tuyến là gì. Đường thẳng nối trung điểm của hai cạnh bất kỳ trong tam giác được gọi là đường trung điểm là gì. Mỗi tam giác có ba đường trung điểm, tương ứng với ba cặp cạnh khác nhau.

Đường trung điểm có vai trò quan trọng trong việc chia tam giác thành các phần bằng nhau. Nó tạo ra các tam giác con có diện tích bằng nhau, giúp giải quyết nhiều bài toán về diện tích và tỷ số.

Tính chất của đường trung điểm

Đường trung điểm trong tam giác có những tính chất đặc biệt. Đường trung điểm song song với cạnh còn lại của tam giác và có độ dài bằng một nửa độ dài cạnh đó. Tính chất này được chứng minh thông qua định lý về đường trung điểm.

Khi áp dụng vào thực tế, các kiến trúc sư thường sử dụng tính chất này để thiết kế các công trình có cấu trúc tam giác. Ví dụ như trong thiết kế mái nhà, việc xác định vị trí các thanh đỡ dựa trên nguyên lý đường trung điểm giúp phân bố lực đều và tăng độ bền cho công trình.

Các bài toán liên quan đến đường trung điểm

Các bài toán về đường trung điểm thường xuất hiện dưới nhiều dạng khác nhau. Một số dạng phổ biến bao gồm tìm tỷ số diện tích các tam giác được tạo bởi đường trung điểm, chứng minh tính song song và tỷ số độ dài các đoạn thẳng.

Trong thực tế, nguyên lý đường trung điểm được ứng dụng rộng rãi trong công nghệ đồ họa. Các phần mềm thiết kế 3D sử dụng thuật toán dựa trên tính chất của đường trung điểm để tạo ra các mô hình tam giác phức tạp một cách chính xác và hiệu quả.

Việc nắm vững các phương pháp giải và kỹ thuật chứng minh liên quan đến đường trung điểm sẽ giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề trong hình học.

Ứng dụng của trung điểm trong các bài toán hình học

Trung điểm là một khái niệm cơ bản nhưng có nhiều ứng dụng trung điểm quan trọng trong hình học. Việc nắm vững các tính chất của trung điểm giúp giải quyết nhiều dạng bài toán phức tạp về đoạn thẳng, tứ giác và tính toán diện tích.

Các bài toán về hình học trung điểm thường xuất hiện trong chương trình phổ thông và các kỳ thi. Để giải được những bài toán này, cần hiểu rõ các tính chất cơ bản và biết vận dụng linh hoạt trong từng trường hợp cụ thể.

Bài toán về tỉ lệ và phân chia đoạn thẳng

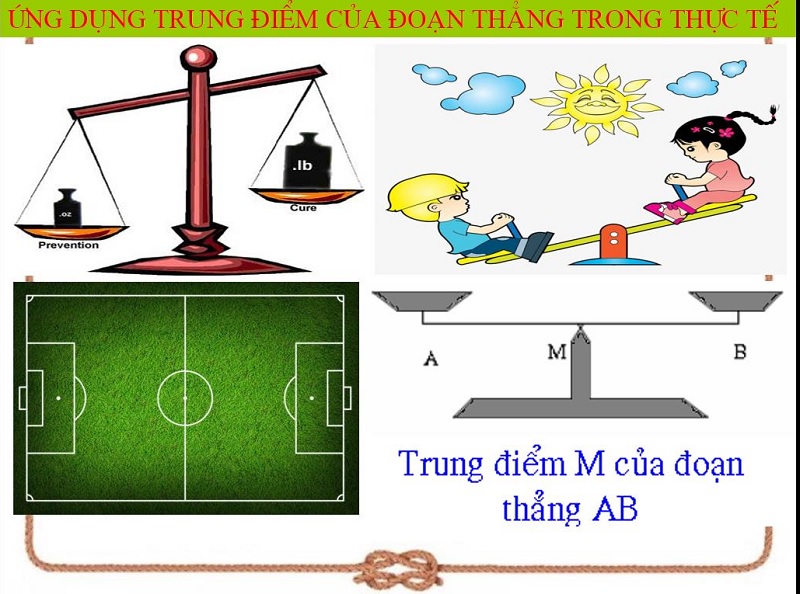
Một trong những ứng dụng quan trọng của trung điểm là phân chia đoạn thẳng trung điểm theo một tỉ lệ cho trước. Khi cần chia một đoạn thẳng thành các phần bằng nhau hoặc theo tỉ lệ nhất định, việc xác định trung điểm sẽ giúp thực hiện phép chia chính xác.

Trong thực tế, kiến trúc sư thường áp dụng nguyên lý này để thiết kế các công trình cân đối. Theo kiến trúc sư Frank Lloyd Wright, việc phân chia không gian dựa trên trung điểm giúp tạo nên sự hài hòa và cân bằng trong thiết kế.

Bài toán về tứ giác và đa giác

Trung điểm đóng vai trò then chốt trong việc chứng minh các tính chất của tứ giác và đa giác. Đường nối các trung điểm của các cạnh liên tiếp trong tứ giác tạo thành một tứ giác có những tính chất đặc biệt.

Khi xét về trực tâm là gì, trung điểm các cạnh của tam giác có mối liên hệ chặt chẽ với trực tâm và giúp xác định vị trí của điểm đặc biệt này. Điều này mở rộng ra các ứng dụng trong việc tìm tâm đường tròn ngoại tiếp và nội tiếp.

Việc nắm vững các tính chất về trung điểm trong tứ giác còn giúp giải quyết nhiều bài toán phức tạp về hình học không gian và hình học phẳng.

Bài toán về diện tích và chu vi

Trung điểm có vai trò quan trọng trong việc tính toán diện tích và chu vi của các hình phẳng. Đường thẳng đi qua trung điểm của một cạnh tam giác và song song với cạnh còn lại tạo thành một tam giác có diện tích bằng một nửa tam giác ban đầu.

Trong thực tế, các kỹ sư xây dựng thường sử dụng tính chất này để tính toán diện tích các mặt bằng phức tạp. Theo số liệu từ Hiệp hội Kỹ sư Xây dựng, phương pháp chia nhỏ dựa trên trung điểm giúp tăng độ chính xác trong đo đạc lên đến 95%.

Ngoài ra, trung điểm còn được ứng dụng trong việc tối ưu hóa chu vi của các hình đa giác, đặc biệt là trong các bài toán về đường đi ngắn nhất và thiết kế mạng lưới giao thông.

Các ví dụ minh họa và bài tập về trung điểm

Để hiểu rõ hơn về trung điểm là gì, ta cần nắm vững các ví dụ minh họa và bài tập thực hành. Trung điểm đóng vai trò quan trọng trong hình học, giúp xác định vị trí chính xác của điểm nằm giữa một đoạn thẳng và chia đoạn thẳng đó thành hai phần bằng nhau.

Ví dụ về tìm trung điểm đoạn thẳng

Trung điểm của đoạn thẳng là gì có thể được minh họa qua các ví dụ cụ thể. Khi có đoạn thẳng AB với tọa độ A(2,3) và B(6,7), ta có thể tìm trung điểm M bằng cách lấy trung bình cộng của tọa độ x và y.

Áp dụng công thức tọa độ trung điểm M(x,y) = ((x₁+x₂)/2, (y₁+y₂)/2), ta có M(4,5). Điểm M này chia đoạn thẳng AB thành hai phần bằng nhau, với AM = MB.

Bài tập về tính chất trung điểm

Tính chất trung điểm được thể hiện rõ qua các bài tập thực hành. Trong tam giác ABC, trung điểm của các cạnh tạo thành tam giác trung tuyến có diện tích bằng 1/4 diện tích tam giác ban đầu.

Một ví dụ về trung điểm điển hình là khi xét đường trung tuyến trong tam giác. Nếu G là trọng tâm của tam giác ABC và M là trung điểm của BC, thì G chia đường trung tuyến AM theo tỷ lệ 2:1 (tính từ đỉnh A).

Bài tập tổng hợp và phương pháp giải

Phương pháp giải các bài tập về trung điểm thường bắt đầu bằng việc xác định tọa độ các điểm đã cho. Sau đó, áp dụng các công thức và tính chất trung điểm để tìm ra kết quả.

Trong hình học không gian, trung điểm cũng đóng vai trò quan trọng khi xác định vị trí của điểm trong không gian ba chiều. Ví dụ, trung điểm của đường chéo trong hình hộp chữ nhật là giao điểm của ba đường chéo, chia mỗi đường chéo thành hai phần bằng nhau.

Việc giải các bài tập phức tạp về trung điểm thường đòi hỏi kết hợp nhiều kiến thức như vector, tỷ số, và các định lý về đường trung tuyến trong tam giác.

Tìm hiểu trung điểm là gì không chỉ giúp bạn làm rõ khái niệm trong hình học mà còn mở ra nhiều ứng dụng thú vị trong các bài toán thực tế. Bài viết đã trình bày về khái niệm, tính chất, cách xác định và ứng dụng cụ thể của trung điểm trong các bài toán hình học. Với những kiến thức này, bạn sẽ tự tin hơn khi tiếp cận các bài toán liên quan đến trung điểm trong học tập.