Hệ phương trình tuyến tính là một kiến thức quan trọng trong toán học. Hệ phương trình này đóng vai trò quan trọng trong nhiều lĩnh vực toán học, khoa học và kỹ thuật, giúp mô hình hóa và giải quyết các bài toán thực tế đa dạng. Cùng Học Thế Nào tìm hiểu về định nghĩa, công thức, cách giải cũng như một số ví dụ minh hoạ cụ thể về hệ phương trình này nhé.
Định nghĩa hệ phương trình tuyến tính
Hệ phương trình tuyến tính là một tập hợp các phương trình đại số. Trong đó mỗi phương trình liên quan đến các biến số được biểu diễn theo dạng tuyến tính. Nó được phân thành 2 dạng cơ bản: dạng tổng quát và dạng thuần nhất.
Dạng tổng quát hệ phương trình tuyến tính
Hệ phương trình tuyến tính bao gồm hai hoặc nhiều phương trình, HPTTT tổng quát có dạng như sau:
$$ \left\{\begin{array}{lc}a_{11}x_1+a_{12}x_2+a_{1n}x_n&=\;b_1\\a_{12}x_1+a_{22}x_2+a_{2n}x_n&=\;b_2\\&…\\a_{m1}x_1+a_{m2}x_2+a_{mn}x_n&=\;b_m\end{array}\right. $$
Trong đó:
- a1,a2,…,an là các hệ số là số thực, a1 khác 0
- x1,x2,…,xn là các ẩn số cần tìm
- b là số hạng tự do

Hệ phương trình tuyến tính thuần nhất
Từ hệ phương trình dạng tổng quát, ta có hệ phương trình tuyến tính thuần nhất. Hệ phương trình tuyến tính thuần nhất là một dạng đặc biệt của hệ phương trình tuyến tính, trong đó vế phải của tất cả các phương trình đều bằng 0. Hệ phương trình này có dạng:
$$ \left\{\begin{array}{lc}a_{11}x_1+a_{12}x_2+a_{1n}x_n&=\;0\\a_{12}x_1+a_{22}x_2+a_{2n}x_n&=\;0\\&…\\a_{m1}x_1+a_{m2}x_2+a_{mn}x_n&=\;0\end{array}\right. $$
Với a1, a2, …, an, b1, b2, …, bn, …, m1, m2, …, mn là các hằng số, x1, x2, …, xn là các ẩn số.
Tính chất:
- Hệ phương trình luôn có ít nhất một nghiệm, đó là nghiệm tầm thường (x1 = 0, x2 = 0, …, xn = 0).
- Hệ phương trình có vô số nghiệm hoặc đúng một nghiệm phi tầm thường khi và chỉ khi hạng của ma trận hệ số nhỏ hơn số ẩn.
- Hệ phương trình có đúng một nghiệm tầm thường khi và chỉ khi hạng của ma trận hệ số bằng số ẩn.
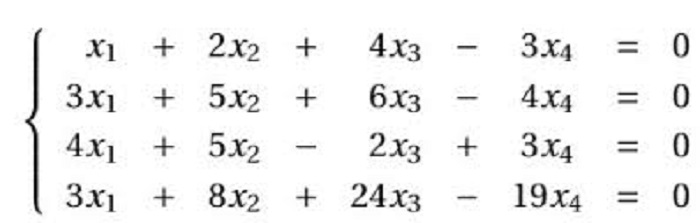
Nghiệm tầm thường, nghiệm không tầm thường là gì?
Trước tiền chúng ta sẽ cùng nhau tìm câu trả lời cho câu hỏi nghiệm tầm thường là gì? Nghiệm không tầm thường là gì?
Khái niệm nghiệm tầm thường
Nghiệm tầm thường là một giải pháp của một phương trình hoặc hệ phương trình mà tất cả các biến đều bằng 0. Nói cách khác, nghiệm tầm thường là khi không có biến nào trong phương trình có giá trị khác 0. Nó còn được gọi là nghiệm hiển nhiên, nghiệm đơn vị, nghiệm null.
Ví dụ:
- Phương trình: 2x + 3y = 6
- Nghiệm tầm thường: x = 0, y = 0
- Hệ phương trình:
2x + y = 4
3x + 2y = 7- Nghiệm tầm thường: x = 0, y = 0

Khái niệm nghiệm không tầm thường
Nghiệm không tầm thường là một giải pháp của một phương trình hoặc hệ phương trình mà ít nhất một biến có giá trị khác 0. Nói cách khác, nghiệm không tầm thường là khi không phải tất cả các biến trong phương trình hoặc hệ phương trình đều bằng 0.
Ví dụ:
- Phương trình: 2x + 3y = 6
- Nghiệm không tầm thường: x = 1, y = 1
- Hệ phương trình:
2x + y = 4
3x + 2y = 7- Nghiệm không tầm thường: x = 1, y = 2
So sánh nghiệm tầm thường và nghiệm không tầm thường
Sau khi đã nắm rõ nghiệm tầm thường là gì, nghiệm không tầm thường là gì. Chúng ta sẽ cùng nhau đi tìm hiểu sự khác biệt của hai loại nghiệm này.
Định nghĩa
- Nghiệm tầm thường thường là nghiệm hiển nhiên, dễ thấy nhất của phương trình, thường có dạng đơn giản như 0 hoặc vector 0.
- Nghiệm không tầm thường là các nghiệm khác 0 hoặc các nghiệm phức tạp hơn, thường đòi hỏi các phương pháp giải phức tạp hơn để tìm ra.
Ý nghĩa toán học
- Nghiệm tầm thường thường tương ứng với trạng thái cân bằng hoặc không có sự thay đổi trong hệ thống.
- Nghiệm không tầm thường thường mô tả các trạng thái hoặc hành vi thú vị hơn của hệ thống.
Phương pháp tìm
- Nghiệm tầm thường thường có thể được xác định bằng cách kiểm tra trực tiếp hoặc bằng trực giác.
- Nghiệm không tầm thường thường đòi hỏi các kỹ thuật giải phương trình phức tạp hơn.

Phân loại phương trình tuyến tính
Có hai tiêu chí để phân loại phương trình tuyến tính đó là theo số lượng ẩn và theo số nghiệm của hệ phương trình. Cụ thể như sau:
Theo số lượng ẩn:
- Hệ một ẩn: Bao gồm một phương trình với một ẩn số.
- Hệ hai ẩn: Bao gồm hai phương trình với hai ẩn số.
- Hệ nhiều ẩn: Bao gồm n phương trình với n ẩn số (n ≥ 3).
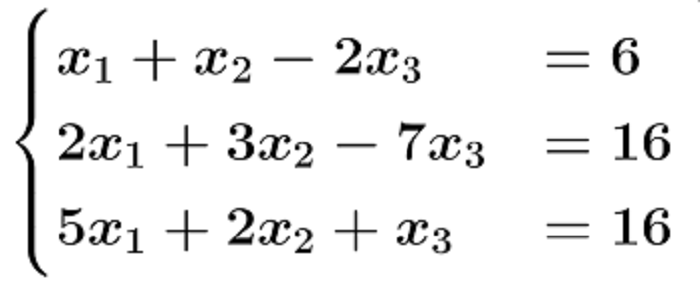
Theo số nghiệm:
- Hệ có vô số nghiệm: Khi tất cả các giá trị của ẩn đều thỏa mãn tất cả các phương trình.
- Hệ có nghiệm duy nhất: Khi chỉ có một tập giá trị duy nhất của ẩn thỏa mãn tất cả các phương trình.
- Hệ vô nghiệm: Khi không có giá trị nào của ẩn thỏa mãn tất cả các phương trình.
Ứng dụng thực tế của hệ phương trình tuyến tính
Hệ phương trình tuyến tính là một công cụ Toán học hữu ích, nó được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Kinh tế: Giải quyết các bài toán về giá cả, lợi nhuận, chi phí,…
- Vật lý: Mô hình hóa các chuyển động, lực, điện,…
- Kỹ thuật: Thiết kế cầu, máy móc, hệ thống điện,…
- Hóa học: Phân tích thành phần hóa học, tính toán nồng độ dung dịch,…
- Sinh học: Mô hình hóa sự phát triển quần thể, phân tích dữ liệu thí nghiệm,…
Cách giải hệ phương trình tuyến tính
Để giải hệ phương trình tuyến tính, bạn có thể áp dụng một trong ba phương pháp phổ biến: phương pháp thế, phương pháp cộng đại số và sử dụng ma trận. Các bước thực hiện cụ thể như sau:
Giải HPTTT bằng phương pháp thế
Bước 1: Chọn ẩn: Chọn một ẩn (thường là ẩn x hoặc y) từ một phương trình bất kỳ (gọi là phương trình thứ nhất) và biểu diễn nó theo ẩn kia.
Bước 2: Thay thế: Thay thế biểu thức của ẩn đã chọn từ bước 1 vào phương trình còn lại (gọi là phương trình thứ hai) để tạo ra phương trình một ẩn.
Bước 3: Giải phương trình một ẩn: Giải phương trình một ẩn thu được ở bước 2 để tìm giá trị của ẩn đã chọn.
Bước 4: Tìm giá trị của ẩn kia: Thay giá trị của ẩn đã tìm được ở bước 3 vào một trong hai phương trình ban đầu để tìm giá trị của ẩn kia.
Ví dụ minh hoạ:
Giải hệ phương trình:
- 2x + 3y = 7
- x – y = 2
Bước 1: Chọn ẩn x từ phương trình thứ nhất và biểu diễn theo y: x = (7 – 3y)/2
Bước 2: Thay x vào phương trình thứ hai: (7 – 3y)/2 – y = 2
Bước 3: Giải phương trình một ẩn: Giải phương trình thu được ở bước 2, ta được y = 1.
Bước 4: Tìm giá trị của x: Thay y = 1 vào phương trình thứ nhất, ta được x = 2.
Kết luận:
Nghiệm của hệ phương trình là (x, y) = (2, 1).
Giải HPTTT bằng phương pháp cộng đại số
Cách giải hệ phương trình tuyến tính bằng phương pháp cộng đại số được thực hiện như sau:
Bước 1: Biến đổi hệ phương trình: Biến đổi hai phương trình ban đầu sao cho hệ số của một ẩn nào đó (thường là x hoặc y) ở hai phương trình bằng nhau hoặc đối nhau.
Bước 2: Loại bỏ một ẩn: Cộng hoặc trừ hai phương trình thu được ở bước 1 để loại bỏ một ẩn, từ đó tạo ra phương trình một ẩn.
Bước 3: Giải phương trình một ẩn: Giải phương trình một ẩn thu được ở bước 2 để tìm giá trị của ẩn đã chọn.
Bước 4: Tìm giá trị của ẩn kia: Thay giá trị của ẩn đã tìm được ở bước 3 vào một trong hai phương trình ban đầu để tìm giá trị của ẩn kia.
Ví dụ minh hoạ:
Giải hệ phương trình:
- 3x + 2y = 11
- x + y = 4
Bước 1: Biến đổi hệ phương trình: Nhân phương trình thứ hai với 3, ta được: 3x + 3y = 12
Bước 2: Loại bỏ ẩn y: Trừ hai phương trình thu được ở bước 1, ta được y = 1.
Bước 3: Tìm giá trị của x: Thay y = 1 vào phương trình thứ nhất, ta được 3x + 2 = 11, giải phương trình này ta được x = 3.
Bước 4: Tìm giá trị của y (không cần thiết vì đã tìm được ở bước 2).
Kết luận: Nghiệm của hệ phương trình là (x, y) = (3, 1).
Giải HPTT bằng ma trận
Để giải hệ phương trình bằng ma trận, trước tiên ta viết hệ phương trình dưới dạng ma trận mở rộng:
[A | B] = [C]
A là ma trận hệ số, B là ma trận cột chứa các vế phải, C là ma trận cột chứa các nghiệm.
Biến đổi ma trận mở rộng về dạng ma trận đơn vị:
[I | D] = [E]
I là ma trận đơn vị, D là ma trận tam giác ngược, E là ma trận cột chứa các nghiệm.
Sau đó thực hiện giải hệ phương trình theo các bước sau:
Bước 1: Biến đổi ma trận mở rộng về dạng ma trận đơn vị
- Sử dụng phép toán Gauss để biến đổi ma trận A về dạng ma trận tam giác trên.
- Nhân ma trận mở rộng với ma trận nghịch đảo của ma trận tam giác trên để thu được ma trận [I | D].
- Tính ma trận E bằng cách nhân ma trận nghịch đảo của ma trận tam giác trên với ma trận C.
Bước 2: Giải ma trận đơn vị
Đọc nghiệm từ ma trận E: Các giá trị trên đường chéo của ma trận E chính là các nghiệm của hệ phương trình.
Ví dụ: Giải hệ phương trình:
- 2x + 3y = 7
- x – y = 2
Bước 1: Biến đổi ma trận mở rộng về dạng ma trận đơn vị:
[ 2 3 | 7 ] [ 1 0 | 2 ] [ 1 0 | 7 ] [ 1 0 | 2 ] [ 1 0 | 5 ]
[ 1 -1 | 2 ] —> [ 0 1 | 2 ] —> [ 0 1 | 2 ] —> [ 0 1 | 1 ] —> [ 0 1 | 5 ]
Bước 2: Giải ma trận đơn vị:
[ 1 0 | 2 ] [ 1 0 | 5 ]
[ 0 1 | 1 ] —> [ 0 1 | 5 ]
Nghiệm của hệ phương trình là (x, y) = (2, 5).
Bài tập củng cố giải hệ PTTT
Dưới đây là phần bài tập hệ phương trình tuyến tính có lời giải dành cho bạn đọc tham khảo:
Bài tập 1: Giải hệ phương trình bằng phương pháp thế:
- 2x + 3y = 7
- x – y = 1
Giải:
Từ phương trình thứ hai, ta có x = y + 1. Thay vào phương trình thứ nhất, ta được:
2(y + 1) + 3y = 7 <=> 5y + 2 = 7 <=> 5y = 5 <=> y = 1
Thay y = 1 vào phương trình thứ hai, ta được:
x – 1 = 1 <=> x = 2
Vậy nghiệm của hệ phương trình là (x, y) = (2, 1).
Bài tập 2: Giải hệ phương trình bằng phương pháp cộng đại số
- 3x + 2y = 11
- x – y = 4
Giải:
Cộng hai phương trình, ta được:
4x + y = 15 <=> y = 15 – 4x
Thay y = 15 – 4x vào phương trình thứ nhất, ta được:
3x + 2(15 – 4x) = 11 <=> -5x + 30 = 11 <=> -5x = -19 <=> x = 19/5
Thay x = 19/5 vào phương trình y = 15 – 4x, ta được:
y = 15 – 4*19/5 <=> y = -11/5
Vậy nghiệm của hệ phương trình là (x, y) = (19/5, -11/5).
Bài tập 3: Giải hệ phương trình:
- 3x + 2y = 11
- x + y = 4
Lời giải:
Bước 1: Biến đổi hệ phương trình về dạng ma trận mở rộng:
[ 3 2 | 11 ]
[ 1 1 | 4 ]
Bước 2: Biến đổi ma trận mở rộng về dạng ma trận đơn vị:
[ 1 0 | 3 ] [ 1 0 | 3 ]
[ 0 1 | 1 ] —> [ 0 1 | 1 ]
Bước 3: Giải ma trận đơn vị:
[ 1 0 | 3 ] [ 1 0 | 3 ]
[ 0 1 | 1 ] —> [ 0 1 | 1 ]
Nghiệm của hệ phương trình là (x, y) = (3, 1).
Lời kết
Hệ phương trình tuyến tính là một công cụ toán học mạnh mẽ với nhiều ứng dụng thực tế. Hy vọng những thông tin mà chúng tôi cung cấp trên đây sẽ giúp bạn nắm vững hơn về lý thuyết cũng như cách giải bài tập trong dạng này.
Nội dung bài viết
- 1. Định nghĩa hệ phương trình tuyến tính
- 2. Nghiệm tầm thường, nghiệm không tầm thường là gì?
- 3. So sánh nghiệm tầm thường và nghiệm không tầm thường
- 4. Phân loại phương trình tuyến tính
- 5. Ứng dụng thực tế của hệ phương trình tuyến tính
- 6. Cách giải hệ phương trình tuyến tính
- 7. Bài tập củng cố giải hệ PTTT
- 8. Lời kết




