Đường chéo hình thang cân làm một khái niệm toán học quan trọng. Những đặc điểm và tính chất của đường chéo mang tính ứng dụng cao, giúp giải quyết nhiều bài toán phức tạp trong lĩnh vực học thuật lẫn thực tiễn cuộc sống hàng ngày. Cùng làm rõ nội dung kiến thức này tại bài viết dưới đây.
Tính chất đường chéo hình thang cân là gì?
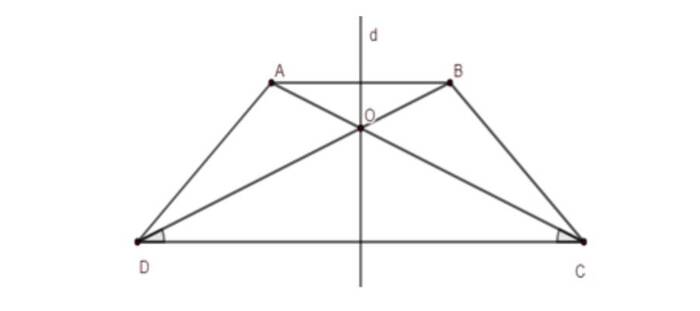
Hình thang cân là chủ thể toán học đặc biệt, sự cân bằng trong hình học tạo nên những tính chất đặc biệt về cạnh, góc và nổi bật là tính chất đường chéo hình thang cân. Dưới đây là một số tính chất cơ bản:
- Hai đường chéo của hình thang cân có độ dài bằng nhau, điều này thể hiện tính đối xứng qua đường chéo của hình thang cân.
- Hai đường chéo của hình thang cân cắt nhau tại điểm đối xứng của hình thang.
- Các đoạn thẳng do hai đường chéo chia ra qua trung điểm O sẽ có tỉ lệ bằng nhau.
- Các góc tạo bởi 2 đường chéo và các cạnh bên của hình thang cân sẽ bằng nhau.
Ví dụ minh họa:
Cho hình thang cân ABCD lấy O là giao điểm của 2 đường chéo AC và BD, dựa vào các tính chất trên ta có:
- AC = BD
- AO/OC = BO/OD
- ∠CAD = ∠DBC; ∠BDA = ∠ACB
Tìm hiểu thêm: htc là gì?cách chứng minh hình thang cân Những đặc điểm và tính chất của hình tam giác
Chứng minh hình thang cân qua 2 đường chéo bằng nhau
Dạng bài này bên cạnh sử dụng dấu hiệu nhận biết hình thang cân, các bạn có thể phát triển bài toán nhằm hướng đến chứng minh các cạnh bên và 2 góc ở đáy bằng nhau (đặc điểm cơ bản của một hình thang cân).
Ví dụ minh họa:
Xét hình thang MNPQ có MP = NQ. Chứng hình MNPQ là hình thang cân.
Hướng dẫn giải:
Từ N kẻ đường thẳng song song với MP và cắt QP tại K.
Ta có hình thang MNKP có hai cạnh bên MP//NK MP = NK. Mà MP = NQ (gt)
⇒ NQ = NK do đó ∆QNK là tam giác cân.
⇒ ∠NQK = ∠NKQ (theo tính chất tam giác cân)
Ta lại có: ∠MPQ = ∠NKQ (hai góc đồng vị)
⇒ ∠NQK = ∠MPQ
Lại xét ∆NQP và ∆MPQ:
- Có NQ = MP (gt)
- ∠NQP = ∠MPQ (đã chứng minh)
- Cạnh QP chung
⇒ ∆NQK = ∆MPQ (c.g.c)
⇒ MQ = NP
Hình thang MNPQ là hình thang cân (tính chất hai cạnh bên bằng nhau)
Có thể bạn quan tâm: dt hình thang cân được tính như thế nào?
Công thức tính đường chéo hình thang cân
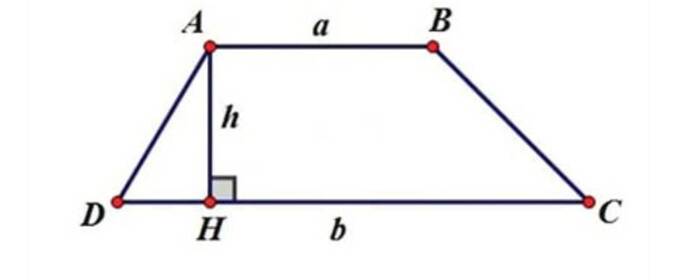
Đường chéo của hình thang cân được tính theo công thức:
$$d=\sqrt{{(\frac{a-b}2)}^2+h^2}$$
Trong đó:
- d: là 2 đường chéo của hình thang cân
- a, b: là độ dài hai cạnh đáy của hình thang cân
- h: là chiều cao của hình thang, vuông góc với cạnh đáy
Để ứng dụng cách tính này, các bạn phải xác định được độ dài các cạnh đáy và chiều cao của hình thang cân kẻ từ đáy nhỏ đến đáy lớn hoặc ngược lại. Công thức trên được suy ra từ định luật Pythagoras.
Lưu ý: Khi áp dụng công thức ta cần đảm bảo độ dài các nhân tố trong công thức có cùng đơn vị đo, nếu không thì phải đổi lại cho chuẩn.
Tìm hiểu thêm: Công thức tính chu vi hình thang cân chuẩn xác
Bài tập minh hoạ cách tính đường chéo hình thang cân
Dưới đây là một số bài tập minh họa về cách tính đường chéo hình thang cân:
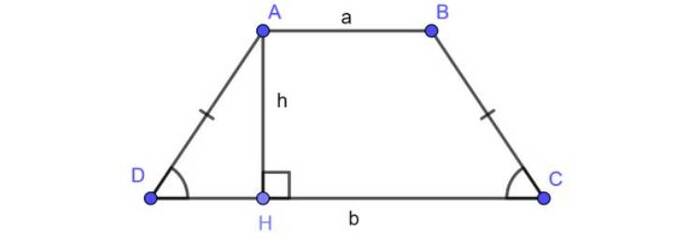
Bài tập minh họa 1: Cho hình thang cân ABCD có AB = 6 cm, CD = 10 cm, AD = BC = 8 cm và chiều cao AH = 8 cm. Tính độ dài hai đường chéo của hình thang cân ABCD?
Hướng dẫn giải:
Áp dụng công thức trên, ta có AC = BD = √[((10-6)/2)^2+8^2] ≈ 8,246 cm.
Bài tập minh họa 2: Cho hình thang cân MNPQ có MN = 4 cm, PQ = 8 cm và diện tích MNPQ là 36 cm^2. Tính độ dài hai đường chéo của hình thang cân MNPQ.
Hướng dẫn giải:
Ta có: S (MNPQ) = ((4+8).h)/2 = 36 ⇔ h = 6 cm. (h là đường cao kẻ từ đỉnh bé đến cạnh lớn của hình thang MNPQ).
Vậy suy ra: độ dài đường chéo MP = NQ = √[((8-4)/2)^2 + 6^2] ≈ 6,325 cm
Trước khi áp dụng công thức, các bạn cần đọc kỹ đề bài, xác định các dữ liệu cần thiết để đưa ra phương hướng giải quyết bài toán tính đường chéo hình thang cân chuẩn xác nhất.
Có thể bạn quan tâm: Cách chứng minh hình thang cân ngắn gọn và chính xác
Ứng dụng đường chéo hình thang cân trong thực tế
Các đặc điểm, tính chất và công thức tính đường chéo của hình thang cân không chỉ có ý nghĩa trong toán học mà chúng còn giúp xử lý các vấn đề quan trọng trong cuộc sống. Cụ thể như:
- Lĩnh vực kiến trúc: Đường chéo của hình thang cân được ứng dụng để thiết kế các cấu trúc như mái vòm, cầu thang hay mái nhà. Việc tính toán chuẩn xác độ dài của đường chéo giúp đảm bảo tính an toàn của công trình và làm hài hòa trong thiết kế.
- Trong ngành kỹ thuật cơ khí: Đường chéo đóng vai trò quan trọng trong việc xác định kích thước và sự cân bằng của các bộ phận máy móc. Nó còn được sử dụng để tính toán sức chịu tải và phân bố trọng lượng trong quá trình thiết kế.
- Trên lĩnh vực thiết kế đồ họa và nghệ thuật: Đường chéo của hình thang cân chơi một vai trò quan trọng trong việc tạo ra sự cân bằng và hài hòa. Từ logo đến cấu trúc trang web và các tác phẩm nghệ thuật khác, đường chéo này không chỉ là công cụ thiết yếu mà còn là yếu tố quan trọng trong việc tối ưu hóa tính cân bằng và đối xứng của các thiết kế.

Các đặc tính đặc biệt như độ dài bằng nhau và điểm giao chia đôi đóng vai trò quan trọng trong việc làm nổi bật sự cân bằng và đối xứng của các cấu trúc và thiết kế này.
Hy vọng những chia sẻ trên đây của chúng tôi sẽ giúp các bạn hiểu hơn về các đặc điểm, tính chất và bài toán đặc trưng của đường chéo hình thang cân. Đừng quên theo dõi bài viết khác của chúng tôi để cập nhật nhiều kiến thức bổ ích!




