Diện tích hình thang cân là kiến thức cơ bản trong chương trình toán học và là tiền đề để học thêm toán nâng cao. Đây là dạng toán xuất hiện nhiều trong bài thi, thậm chí là trong ứng dụng đời sống thực tế. Để hỗ trợ bạn nắm chắc kiến thức hơn, hocthenao đã tổng hợp chi tiết công thức, phương pháp tính toán đi kèm ví dụ cụ thể ở bài viết dưới đây. Mời bạn đọc cùng tìm hiểu nhé!
Công thức tính diện tích hình thang cân
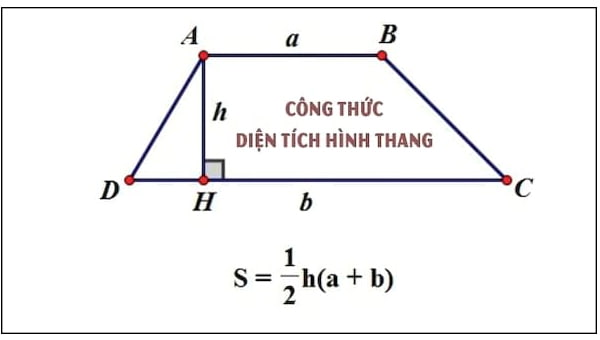
Hình thang cân là một dạng hình thang nhưng mang đặc điểm riêng có 2 cạnh bên độ dài bằng nhau. Để tính diện tích hình thang cân, bạn hãy áp dụng đúng công thức sau:
$$S=\frac{a+b}2\times h$$
Trong đó:
- a là độ dài của cạnh đáy nhỏ
- b là độ dài của cạnh đáy lớn
- h là chiều cao của hình thang
- S là diện tích
Ví dụ cụ thể: Cho một hình thang cân MNPQ có cạnh đáy nhỏ là MN 6cm, cạnh đáy lớn QP là 8cm, chiều cao h là 4cm. DT hình thang cân MNPQ là bao nhiêu?
Giải
Áp dụng công thức ta có:
$$S=\frac{a+b}2x\;h\;=\frac{20+14}2\times8=136\;cm^2$$
=> Diện tích hình thang cân MNPQ là 28 cm2
Xem thêm: Cách tính chu vi hình thang cân và ví dụ minh hoạ
Các yếu tố ảnh hưởng đến kết quả tính diện tích hình thang cân
Bên cạnh công thức tính diện tích hình thang cân, bạn cũng cần lưu ý một số yếu tố có thể ảnh hưởng đến kết quả cuối cùng khi làm phép toán. Bởi nếu nhầm 1 trong 2 số liệu này thì sẽ rất dễ bị sai.
- Độ dài của hai đáy: Hai cạnh song song của hình thang cân hay còn gọi là đáy lớn và đáy bé. Thay đổi số liệu độ dài sẽ ảnh hưởng trực tiếp đến kết quả tính diện tích hình.
- Chiều cao (h): Chiều cao của hình thang cân là khoảng cách vuông góc từ đáy này đến đáy kia. Chiều cao càng lớn thì diện tích hình thang càng lớn.
Có thể thấy rằng những thay đổi về kích thước của các cạnh này sẽ ảnh hưởng trực tiếp đến kết quả tính diện tích và chúng có mối liên hệ chặt chẽ với nhau.
Lưu ý khi tính diện tích hình thang cân
Một số lưu ý khi tính diện tích của hình thang cân dưới đây bạn cần lưu tâm để có kết quả chính xác nhất.
- Xác định chính xác độ dài hai cạnh đáy và chiều cao để tránh sai khi áp dụng công thức. Chiều cao là đường kẻ từ đỉnh xuống cạnh đáy và vuông góc với cạnh đáy đó.
- Sử dụng đúng công thức $$S=\frac{a+b}2\times h$$ và xác định đúng các thành phần trong công thức (a, b là 2 cạnh đáy và h là chiều cao)
- Chú ý đến đơn vị đo của từng cạnh trong bài toán, nếu khác nhau cần đổi về một loại đơn vị đo rồi mới đặt phép tính.
- Trường hợp đề bài không cho đủ thông tin cần tính theo công thức, cần đọc kỹ đề và tìm cách tính các cạnh còn lại.
- Học bài kỹ để hiểu về định nghĩa, tính chất là điều quan trọng giúp việc áp dụng công thức tính toán trở nên dễ dàng và chính xác hơn.
Tìm hiểu thêm: Cách chứng minh hình thang cân hay và chi tiết
Bài tập ứng dụng cách tính dt hình thang cân
Dưới đây là một số bài tập đi kèm cách tính diện tích hình thang cân cụ thể:
Bài Tập 1
Cho hình thang cân ABCD có:
- Đáy lớn (AB = 12 cm)
- Đáy nhỏ (CD = 8 cm)
- Chiều cao (h = 5 cm)
Hãy tính diện tích của hình thang cân ABCD.
Giải
Sử dụng công thức tính diện tích hình thang: $$S=\frac{a+b}2\times h =>S=\frac{12+8}2\times5=50\;cm^2$$
Vậy diện tích của hình thang cân ABCD là 50cm2
Bài Tập 2
Cho hình thang cân EFGH có chiều dài đáy lớn EF là 20cm, chiều dài đáy nhỏ GH là 14cm, chiều cao h là 8cm. Hãy tính diện tích của hình thang cân EFGH.
Giải
Sử dụng công thức :$$S=\frac{a+b}2\times h => S=\frac{20+14}2\times8=136\;cm^2$$
Vậy diện tích của hình thang cân ABCD là 136 cm2

Xem ngay: Tính chất, dhnb hình thang cân và cách chứng minh
Những ứng dụng của dt hình thang cân trong thực tế
Hình thang cân không chỉ là một dạng hình học mà còn có nhiều ứng dụng thực tế trong đời sống và các lĩnh vực khác nhau:
- Xây dựng cầu đường: Hình thang cân thường được sử dụng trong thiết kế mặt cắt ngang của cầu và đường. Cấu trúc hình thang giúp phân phối trọng lượng và lực đều đặn nhằm tăng độ bền cho công trình.
- Thiết kế kiến trúc: Được sử dụng để tạo ra các cấu trúc độc đáo cho mái nhà, cửa sổ, hoặc các chi tiết trang trí. Sự cân đối của hình thang mang lại cảm giác hài hòa và tính thẩm mỹ cao.
- Kỹ thuật cơ khí: Hình thang cân được áp dụng trong thiết kế các bộ phận máy móc, đặc biệt là các thành phần chịu lực và cần độ ổn định cao. Ví dụ như các bánh răng hoặc trục có hình thang
- Khoa học và giáo dục: Hình thang cân được sử dụng trong sách giáo khoa và tài liệu học tập để giảng dạy về tính chất hình học, tính toán diện tích, chu vi,…
- Nghệ thuật và thiết kế đồ họa: Với ứng dụng này, hình thang cân được sử dụng để tạo ra các bố cục cân đối và hài hòa.
Bên cạnh đó, những kiến thức về hình thang cân còn giúp chúng ta phát triển tư duy hình học một cách logic.
Trên đây là những thông tin chi tiết về công thức và cách tính diện tích hình thang cân. Việc nắm chắc kiến thức cơ bản này sẽ giúp bạn có một nền tảng vững chắc để đạt những thành tích cao hơn trong học tập. Đừng quên theo dõi những bài viết khác của hocthenao để khám phá thêm nhiều kiến thức bổ ích nhé.




