Đường chéo hình thoi: Khái niệm, công thức và ứng dụng trong toán học

Đường chéo hình thoi là yếu tố quan trọng trong hình học, kết nối hai đỉnh đối diện của hình thoi. Bài viết này sẽ khám phá các tính chất, công thức tính và ứng dụng thực tiễn của đường chéo hình thoi. Hãy cùng tìm hiểu để áp dụng kiến thức vào học tập và giải toán hiệu quả.

Đường chéo hình thoi là đoạn thẳng nối hai đỉnh đối diện của hình thoi

Đường chéo hình thoi là các đoạn thẳng nối hai đỉnh đối diện của hình thoi. Mỗi hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm. Đường chéo lớn là đường chéo dài hơn, đường chéo nhỏ là đường chéo ngắn hơn.

Một tính chất quan trọng của đường chéo của hình thoi là chúng luôn vuông góc và chia đôi lẫn nhau. Điều này có nghĩa là hai đường chéo sẽ tạo thành góc 90 độ khi giao nhau và điểm giao nhau chính là trung điểm của cả hai đường chéo. Tính chất này giúp việc tính diện tích hình thoi trở nên đơn giản hơn.

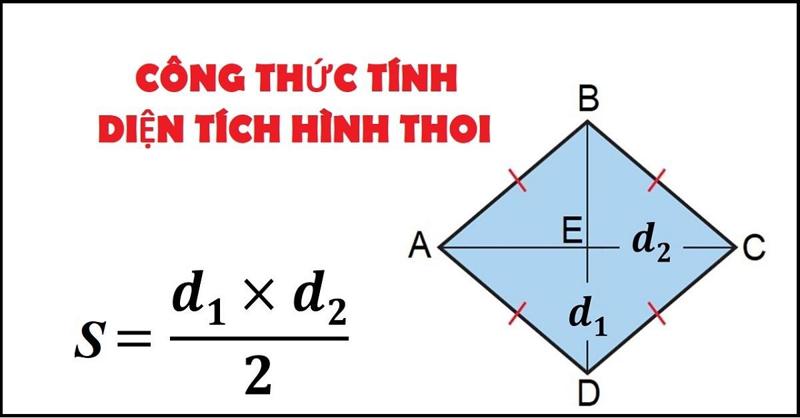
Đường chéo của hình thoi còn có vai trò quan trọng trong việc xác định tâm đối xứng của hình. Điểm giao nhau của hai đường chéo chính là tâm đối xứng của hình thoi. Từ đó, ta có thể xác định được các cặp điểm đối xứng qua tâm và các đường thẳng đối xứng của hình thoi.

Tính chất quan trọng của đường chéo hình thoi trong hình học phẳng

Trong Hình học phẳng, tính chất đường chéo hình thoi đóng vai trò then chốt giúp phân biệt hình thoi với các tứ giác khác. Các đặc điểm của đường chéo không chỉ xác định hình dạng mà còn quyết định nhiều tính chất quan trọng của hình thoi.

2 đường chéo hình thoi tạo nên cấu trúc đặc biệt bên trong hình, giúp chứng minh nhiều bài toán phức tạp trở nên đơn giản hơn. Các tính chất này được ứng dụng rộng rãi trong thiết kế kiến trúc và nghệ thuật trang trí.

Hai đường chéo hình thoi vuông góc với nhau

Tính chất vuông góc của hai đường chéo là đặc trưng nổi bật nhất của hình thoi. Khi hai đường chéo cắt nhau, chúng tạo thành góc 90 độ, phân chia hình thoi thành 4 tam giác cân bằng nhau.

Tính chất này được ứng dụng nhiều trong kiến trúc, như thiết kế mái vòm của nhà thờ Duomo ở Florence – Italy. Kiến trúc sư Filippo Brunelleschi đã khéo léo sử dụng nguyên lý vuông góc của đường chéo hình thoi để tạo nên kết cấu vững chắc cho công trình.

Hai đường chéo hình thoi cắt nhau tại trung điểm

Đường chéo của hình thoi luôn cắt nhau tại trung điểm, chia đôi lẫn nhau thành các đoạn bằng nhau. Điểm giao của hai đường chéo trở thành tâm đối xứng của hình thoi.

Tính chất này tạo nên sự cân bằng hoàn hảo cho hình thoi. Trong nghệ thuật trang trí Islamic, các nghệ nhân thường sử dụng mô típ hình thoi với đường chéo cắt nhau tại trung điểm để tạo nên những hoa văn đối xứng tinh tế.

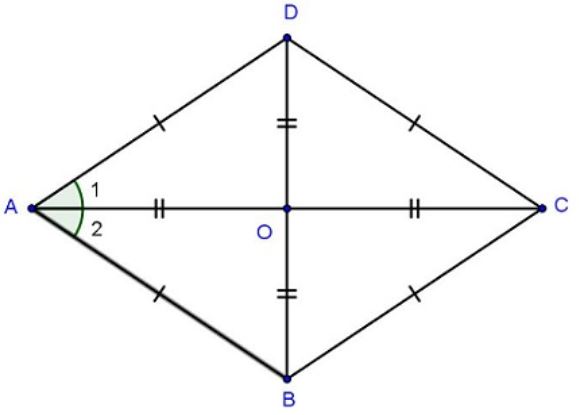
Đường chéo hình thoi chia đôi các góc của hình thoi

Mỗi đường chéo của hình thoi đều chia đôi góc tại đỉnh mà nó đi qua. Điều này tạo nên 4 tam giác đồng dạng, có diện tích bằng nhau trong hình thoi.

Trong thiết kế logo, nhiều thương hiệu nổi tiếng như Renault đã tận dụng tính chất này để tạo ra biểu tượng cân đối và hài hòa. Các góc được chia đều tạo cảm giác về sự hoàn chỉnh và chuyên nghiệp trong nhận diện thương hiệu.

Tính chất này còn giúp đơn giản hóa việc tính toán diện tích và các yếu tố khác của hình thoi, đặc biệt trong các bài toán hình thoi trong hình học nâng cao.

Công thức tính độ dài đường chéo hình thoi và ứng dụng

Hình thoi là gì là một tứ giác đặc biệt với 4 cạnh bằng nhau. Để tính được đường chéo của hình thoi, ta cần nắm vững các công thức cơ bản dựa trên các yếu tố như cạnh, góc và diện tích. Việc tính toán đường chéo hình thoi có vai trò quan trọng trong nhiều bài toán thực tế như thiết kế, xây dựng và kiến trúc.

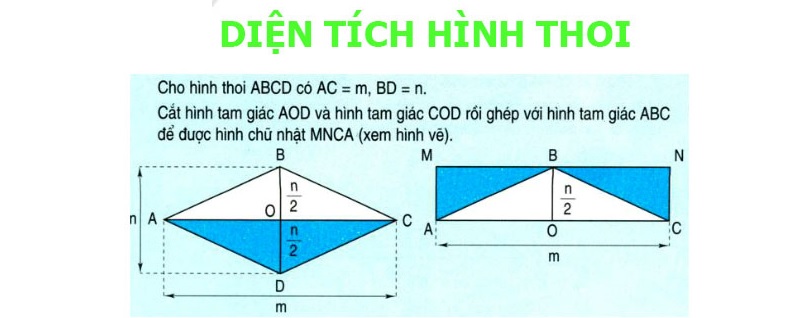
Công thức tính đường chéo hình thoi qua cạnh và góc

Cách tính đường chéo hình thoi thông qua cạnh và góc sử dụng công thức d1 = 2a.sin(α/2) và d2 = 2a.cos(α/2), trong đó:

• d1 là đường chéo thứ nhất
• d2 là đường chéo thứ hai
• a là độ dài cạnh hình thoi
• α là góc giữa hai đường chéo

Ngoài ra, ta còn có thể sử dụng công thức d1 = 2a.sin(α) và d2 = 2a.cos(α) khi biết góc α giữa cạnh và đường chéo.

Công thức tính đường chéo hình thoi qua diện tích

Công thức tính đường chéo hình thoi qua diện tích được xác định bởi S = (d1.d2)/2, trong đó S là diện tích hình thoi, d1 và d2 là hai đường chéo. Từ đó, ta có thể suy ra:

• Nếu biết một đường chéo d1 và diện tích S, đường chéo còn lại d2 = 2S/d1
• Nếu biết diện tích S và tỉ số k = d1/d2, ta có d1 = √(2kS) và d2 = √(2S/k)

Việc áp dụng công thức này đặc biệt hữu ích khi giải các bài toán liên quan đến diện tích.

Bài tập áp dụng tính đường chéo hình thoi

Để thực hành tính đường chéo hình thoi, ta xét ví dụ sau: Cho hình thoi có cạnh 5cm và góc nhọn 60°.

Áp dụng công thức:
d1 = 2a.sin(60°) = 2.5.0,866 = 8,66cm
d2 = 2a.cos(60°) = 2.5.0,5 = 5cm

Một ví dụ khác: Hình thoi có diện tích 24cm² và một đường chéo d1 = 6cm.
Áp dụng công thức S = (d1.d2)/2:
24 = (6.d2)/2
→ d2 = 8cm

Các bài tập này minh họa cách vận dụng linh hoạt các công thức tùy theo dữ kiện được cho.

Mối quan hệ giữa đường chéo và các yếu tố khác của hình thoi

Đường chéo hình thoi có mối liên hệ mật thiết với các yếu tố khác trong hình học. Hai đường chéo của hình thoi luôn vuông góc và cắt nhau tại trung điểm, tạo nên 4 tam giác bằng nhau. Đặc điểm này tương tự như đường chéo hình tam giác cân khi chia hình thành các phần đối xứng.

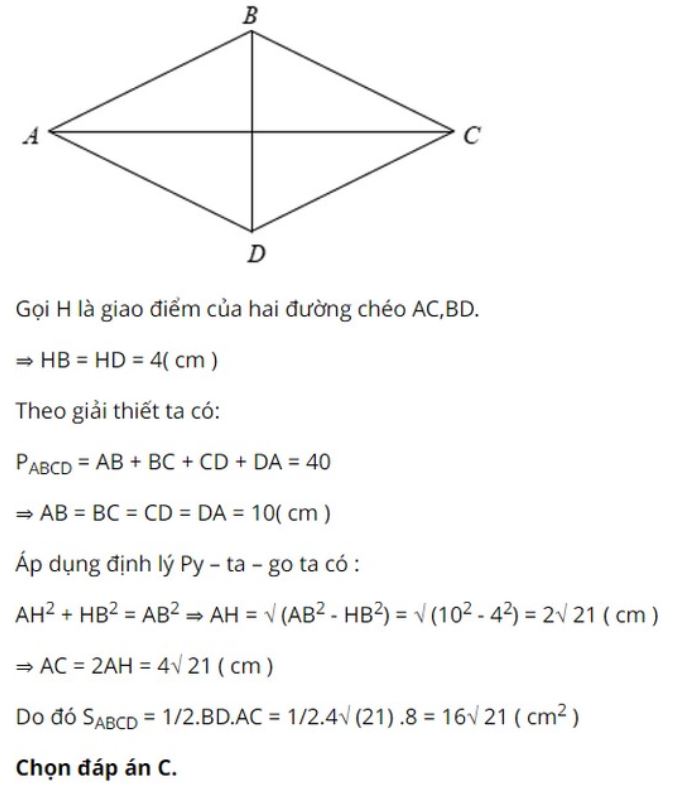
Các đường chéo của hình thoi đóng vai trò quan trọng trong việc xác định diện tích, góc và các tính chất hình học khác. Mối quan hệ này được thể hiện qua 3 khía cạnh chính: diện tích, chu vi và góc.

Đường chéo và diện tích hình thoi

Diện tích của hình thoi được tính bằng tích của hai đường chéo chia cho 2. Công thức này dựa trên nguyên lý hình học cơ bản khi hai đường chéo vuông góc với nhau tạo thành 4 tam giác đồng dạng.

Khi một đường chéo thay đổi độ dài, diện tích hình thoi sẽ thay đổi tỷ lệ thuận, trong khi đường chéo còn lại giữ nguyên. Điều này cho phép tạo ra nhiều hình thoi khác nhau với cùng một chu vi nhưng diện tích khác nhau.

Đường chéo và chu vi hình thoi

Tính chu vi hình thoi không phụ thuộc trực tiếp vào độ dài các đường chéo. Thay vào đó, chu vi được xác định bằng độ dài cạnh nhân với 4, do các cạnh của hình thoi bằng nhau.

Tuy nhiên, độ dài đường chéo có ảnh hưởng gián tiếp đến cạnh hình thoi thông qua định lý Pytago. Khi biết độ dài hai đường chéo, có thể tính được độ dài cạnh và từ đó tính được chu vi.

Đường chéo và các góc của hình thoi

Hai đường chéo của hình thoi chia các góc thành hai phần bằng nhau. Góc giữa hai đường chéo luôn là 90 độ, tạo nên tính đối xứng hoàn hảo cho hình.

Khi tỷ lệ độ dài giữa hai đường chéo thay đổi, các góc của hình thoi cũng thay đổi theo. Nếu hai đường chéo bằng nhau, hình thoi trở thành hình vuông với bốn góc đều bằng 90 độ. Ngược lại, khi một đường chéo ngắn hơn nhiều so với đường chéo còn lại, hình thoi sẽ có hai góc nhọn và hai góc tù đối diện nhau.

Ứng dụng của đường chéo hình thoi trong thực tế và bài toán hình học

Đường chéo hình thoi có nhiều ứng dụng quan trọng trong cuộc sống và toán học. Hai đường chéo vuông góc và cắt nhau tại trung điểm tạo nên những đặc tính độc đáo, giúp ích cho nhiều lĩnh vực từ thiết kế đến xây dựng và giải toán.

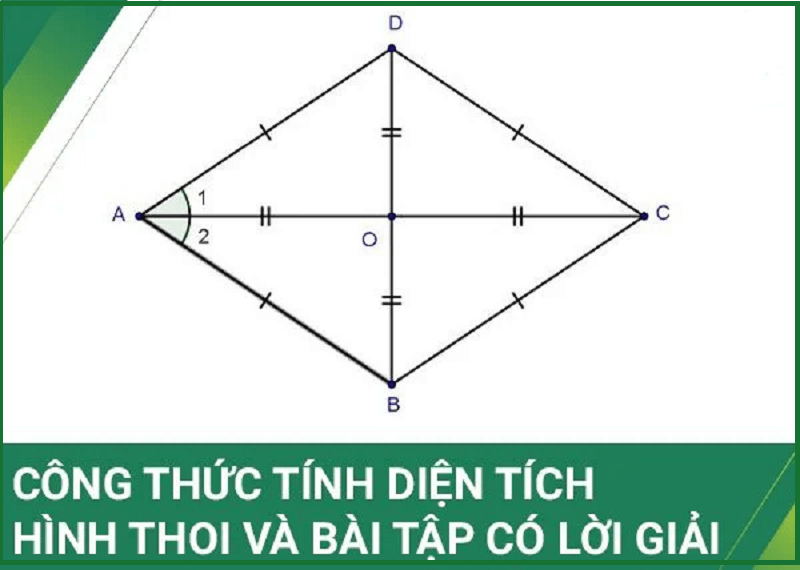
Các đặc điểm hình thoi như tính đối xứng qua đường chéo và sự vuông góc giữa hai đường chéo tạo điều kiện thuận lợi cho việc tính toán diện tích và thiết kế các công trình. Điều này làm cho hình thoi trở thành một hình học cơ bản nhưng có nhiều giá trị ứng dụng thực tiễn.

Ứng dụng trong thiết kế và xây dựng

Trong kiến trúc, hình thoi thường được sử dụng để thiết kế các mái vòm, cửa sổ và các chi tiết trang trí. Công trình Louvre Abu Dhabi là một ví dụ điển hình, với mái vòm được tạo thành từ hàng nghìn mảnh hình thoi đan xen, tạo nên hiệu ứng ánh sáng độc đáo.

Các kỹ sư cầu đường cũng áp dụng nguyên lý của ứng dụng hình thoi trong việc thiết kế các kết cấu dàn thép. Đường chéo của hình thoi giúp phân phối lực đều và tăng độ bền cho công trình. Điều này có thể thấy rõ trong cấu trúc của cầu Sydney Harbour Bridge.

Ứng dụng trong giải toán hình học phẳng

Trong hình học phẳng, đường chéo hình thoi đóng vai trò quan trọng trong việc giải các bài toán về diện tích và góc. Tương tự như đường chéo hình lập phương, đường chéo hình thoi cung cấp những công thức tính toán đơn giản và hiệu quả.

Việc sử dụng tính chất vuông góc của đường chéo giúp đơn giản hóa nhiều bài toán phức tạp. Đặc biệt trong các bài toán chứng minh, tính chất này thường được sử dụng như một công cụ hữu hiệu để chứng minh sự bằng nhau của các đoạn thẳng hoặc góc.

Bài tập thực hành về đường chéo hình thoi

Để nắm vững kiến thức về đường chéo hình thoi, học sinh cần thực hành qua các dạng bài tập đa dạng. Các bài tập thường tập trung vào việc tính toán độ dài đường chéo, diện tích và các yếu tố liên quan.

Một số bài tập yêu cầu vận dụng tính chất đường chéo để chứng minh các mệnh đề hình học. Những bài tập này giúp phát triển tư duy logic và khả năng phân tích hình học của học sinh.

Việc giải quyết các bài toán thực tế liên quan đến hình thoi cũng rất quan trọng. Ví dụ như tính diện tích của một mảnh kính hình thoi trong thiết kế cửa sổ, hay tính toán kích thước của các tấm panel năng lượng mặt trời hình thoi.

Đường chéo hình thoi không chỉ là đoạn thẳng nối hai đỉnh đối diện mà còn có nhiều tính chất quan trọng trong hình học. Các công thức tính toán độ dài đường chéo cùng với ứng dụng thực tiễn đã được đề cập rõ ràng. Việc nắm vững đường chéo hình thoi sẽ giúp học sinh củng cố kiến thức và áp dụng vào các bài toán hình học một cách hiệu quả hơn.