Biểu diễn hình học của số phức giúp ta dễ dàng hình dung và thao tác với số phức trong các bài toán phức tạp. Số phức là một nhánh mở rộng của số thực, không chỉ trừu tượng trên giấy tờ, số phức còn có thể được biểu diễn trực quan bằng hình ảnh, mở ra cánh cửa khám phá thế giới đại số học huyền ảo và đầy hấp dẫn. Bài viết dưới đây của Học Thế Nào sẽ giúp bạn tìm hiểu về biểu diễn hình học số phức, từ định nghĩa cơ bản đến những ứng dụng thú vị của nó trong Toán học.
Định nghĩa số phức và điểm biểu diễn hình học
Như chúng ta đã biết, số phức z được biểu diễn dưới dạng z = a + bi, với a và b là số thực, i là đơn vị ảo thỏa mãn $$i^2=-1$$ Số phức z được biểu diễn trong mặt phẳng Oxy bởi điểm M(a, b) như sau:
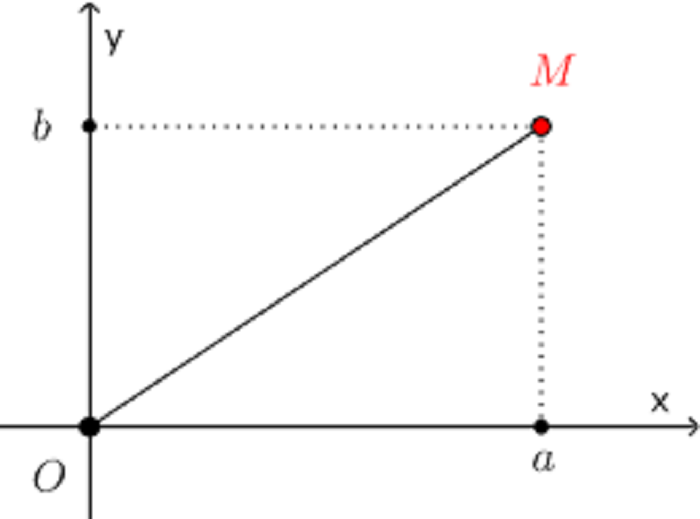
Đối với dạng Toán này, chúng ta thường xuyên gặp phải những bài tập yêu cầu tìm tập hợp điểm biểu diễn của số phức z trên mặt phẳng toạ độ. Trong đó số phức z này cần phải thoả mãn một hệ thức cho trước theo yêu cầu của đề bài (thường liên quan tới môđun của số phức z). Dạng bài tập này được giải theo cách sau:
Giả sử ta có số phức z = x+yi (x, y ∈ R). Khi đó, điểm M có toạ độ (a;b) là điểm biểu diễn số phức z trên mặt phẳng Oxy. Với việc sử dụng những dữ kiện mà đề bài cho, chúng ta có thể tìm mối liên hệ giữa x và y từ đó tìm ra tập hợp toạ độ của điểm M.
Các khái niệm liên quan
Để giải được những bài toán liên quan đến hình học số phức, bạn cần nắm được những khái niệm cơ bản sau đây:
- Số phức liên hợp: Số phức liên hợp của z = a + bi là z¯ = a – bi.
- Môđun của số phức: Mô đun của số phức z được ký hiệu là |z| và bằng $$\vert z\vert=\sqrt{\left(a^2+b^2\right)}$$ là khoảng cách từ điểm M(a, b) đến gốc O.
- Lượng giác của số phức: Lượng giác của số phức z được ký hiệu là arg(z) và bằng arg(z) = arctan(b/a), là góc tạo bởi tia OM và trục Ox dương.

Phép toán và liên hệ hình học
Dạng toán biểu diễn hình học số phức bao gồm các phép toán chủ yếu như:
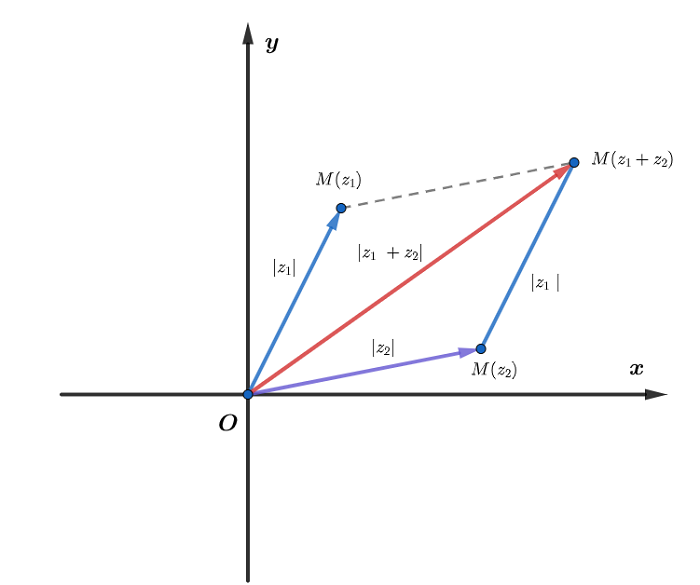
- Phép cộng và trừ: Phép cộng và trừ số phức được thực hiện tương tự như số thực, bằng cách cộng trừ các phần thực và ảo riêng biệt. Trên mặt phẳng Oxy, phép cộng và trừ số phức được biểu diễn bằng phép di chuyển điểm biểu diễn.
- Phép nhân: Phép nhân số phức được thực hiện theo công thức (a + bi)(c + di) = (ac – bd) + (ad + bc)i. Trên mặt phẳng Oxy, phép nhân số phức được biểu diễn bằng phép biến đổi hình học, bao gồm phép quay và phép giãn nở.
- Phép chia: Phép chia số phức được thực hiện bằng cách chia cả tử và mẫu cho số phức liên hợp của mẫu. Trên mặt phẳng Oxy, phép chia số phức được biểu diễn bằng phép biến đổi hình học, bao gồm phép quay và phép co.
Ứng dụng biểu diễn hình học của số phức
Biểu diễn hình học của số phức có nhiều ứng dụng hữu ích trong Toán học, Vật lý cùng nhiều lĩnh vực khác, chẳng hạn như:
- Giải phương trình: Biểu diễn hình học giúp trực quan hóa quá trình giải phương trình số phức, đặc biệt là phương trình bậc hai. Nó còn được sử dụng để giải hệ phương trình tuyến tính phức tạp bằng cách biến đổi hình học.
- Hình học phức: Giúp trực quan hóa các đường cong phức như đường tròn, parabol, hyperbol,… và nghiên cứu các tính chất của chúng. Ngoài ra nó còn giúp chúng ta nghiên cứu các mặt phẳng phức, bao gồm phép biến đổi, phép đồng dạng, phép dời chỗ,…
- Điện tích: Trong điện tích, số phức được sử dụng để mô tả dòng điện xoay chiều, giúp tính toán các đại lượng điện áp, dòng điện, và công suất.
Trong đời sống, biểu diễn hình học được sử dụng trong nhiều lĩnh vực kỹ thuật như xử lý tín hiệu, điều khiển hệ thống, và hệ thống truyền thông. Thậm chí nó còn được sử dụng trong một số mô hình kinh tế để mô tả các hiện tượng phức tạp như thị trường tài chính và hành vi của người tiêu dùng hay sử dụng trong đồ họa máy tính để tạo ra các hình ảnh và hiệu ứng 3D phức tạp.
Bài tập tìm tập hợp điểm biểu diễn số phức
Dưới đây là một số bài tập dạng tìm tập hợp điểm biểu diễn số phức giúp bạn làm quen tốt hơn với dạng toán này:
Bài tập 1: Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z – 3 – 4i| = 2.
Giải:
Gọi M(a, b) là điểm biểu diễn số phức z. Theo đề bài, ta có:
|z – (3 – 4i)| = 2
Điều này có nghĩa là M(a, b) cách điểm A(3, -4) một khoảng bằng 2. Đây là đường tròn tâm A(3, -4) và bán kính bằng 2.
Kết luận: Tập hợp điểm biểu diễn số phức z thỏa mãn |z – 3 – 4i| = 2 là đường tròn tâm A(3, -4) và bán kính bằng 2.
Bài tập 2: Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z + 2i| = |z – i|.
Giải:
Gọi M(a, b) là điểm biểu diễn số phức z. Theo đề bài, ta có:
|z + 2i| = |z – i|
Điều này có nghĩa là MA = MB, với M là điểm biểu diễn số phức z, A là điểm biểu diễn số phức -2i, và B là điểm biểu diễn số phức i.
Kết luận: Tập hợp điểm biểu diễn số phức z thỏa mãn |z + 2i| = |z – i| là đường trung trực của đoạn thẳng AB, với A là điểm biểu diễn số phức -2i và B là điểm biểu diễn số phức i.
Bài tập 3: Tìm số phức z thỏa mãn z + 2z¯ = 5 – 3i.
Giải:
Gọi z = a + bi, với a và b là số thực. Ta có:
z + 2z¯ = 5 – 3i
⇔ (a + bi) + 2(a – bi) = 5 – 3i
⇔ 3a = 5
⇔ a = 5/3
⇔ z = 5/3 + bi
Kết luận: Số phức z thỏa mãn z + 2z¯ = 5 – 3i là z = 5/3 + bi, với b là số thực bất kỳ.
Bài tập trắc nghiệm
Một số câu hỏi trắc nghiệm về dạng biểu diễn hình học số phức:
Câu 1: Cho số phức z thỏa mãn |z – 3 – 4i| = 2. Tập hợp điểm biểu diễn số phức z là:
A. Đường tròn tâm A(3, -4) và bán kính bằng 2.
B. Đường tròn tâm O(0, 0) và bán kính bằng 2.
C. Đường thẳng x = 3.
D. Đường thẳng y = -4.
Câu 2: Cho số phức z thỏa mãn |z + 2i| = |z – i|. Tập hợp điểm biểu diễn số phức z là:
A. Đường tròn tâm O(0, 0) và bán kính bất kỳ.
B. Đường trung trực của đoạn thẳng AB, với A là điểm biểu diễn số phức -2i và B là điểm biểu diễn số phức i.
C. Đường thẳng x = 1.
D. Đường thẳng y = -1.
Câu 3: Số phức z thỏa mãn z + 2z¯ = 5 – 3i là:
A. z = 5/3 + bi, với b là số thực bất kỳ.
B. z = -5/3 + bi, với b là số thực bất kỳ.
C. z = 5/3 – bi, với b là số thực bất kỳ.
D. z = -5/3 – bi, với b là số thực bất kỳ.
Câu 4: Cho số phức z thỏa mãn |z – 2| + |z + 3| = 5. Tập hợp điểm biểu diễn số phức z là:
A. Đường tròn tâm O(0, 0) và bán kính bằng 5.
B. Đường thẳng x = 0.
C. Đường hypebol có hai tiêu điểm là A(2, 0) và B(-3, 0), và có độ dài trục chính bằng 5.
D. Đường ellipse có hai tiêu điểm là A(2, 0) và B(-3, 0), và có độ dài trục chính bằng 5.
Câu 5: Gọi M là điểm biểu diễn số phức z, A là điểm biểu diễn số phức 3 + 4i, và B là điểm biểu diễn số phức -2 – i. Tam giác MAB vuông cân tại M khi và chỉ khi:
A. |z| = 5.
B. |z – 3 – 4i| = |z + 2 + i|.
C. Arg(z – 3 – 4i) = Arg(z + 2 + i).
D. z thỏa mãn phương trình z^2 – 5z + 6 = 0.
Lời giải:
- A
- B
- A
- C
- B
Kết luận
Biểu diễn hình học của số phức là một công cụ vô cùng hữu ích trong Toán học, giúp giải quyết các bài toán phức tạp, khám phá những bí ẩn của thế giới số phức, và mở ra cánh cửa đến những ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Hiểu rõ về biểu diễn hình học sẽ giúp bạn chinh phục những bài tập khó nhằn nhất trong chương cuối cùng của chương trình Đại số 12.




