Công thức cấp số cộng và các phương pháp tính toán cơ bản trong dãy số

Công thức cấp số cộng là một khái niệm cơ bản trong toán học, liên quan đến dãy số với sự khác biệt đều giữa các số hạng. Nhận biết công thức tính hệ số và tổng của cấp số cộng sẽ giúp bạn nắm vững kiến thức và áp dụng hiệu quả trong giải toán. Khám phá chi tiết về các công thức và phương pháp tính trong bài viết này.

Công thức cấp số cộng và các khái niệm cơ bản trong dãy số

Cấp số cộng là gì – một dãy số mà mỗi số hạng (trừ số hạng đầu tiên) bằng số hạng liền trước cộng với một số không đổi d, được gọi là công sai của dãy số. Ví dụ: 2, 5, 8, 11, 14,… là một cấp số cộng với công sai d = 3.

Để xác định một công thức cấp số cộng, ta cần biết số hạng đầu tiên (a₁) và công sai (d). Từ đó có thể tính được số hạng thứ n theo công thức: aₙ = a₁ + (n-1)d. Công thức này giúp ta tìm được bất kỳ số hạng nào trong dãy số mà không cần phải liệt kê tất cả các số hạng trước đó.

Ngoài ra, để tính tổng n số hạng đầu tiên của cấp số cộng, ta có thể áp dụng công thức tính tổng dãy số với công thức: Sₙ = n(a₁ + aₙ)/2 hoặc Sₙ = n[2a₁ + (n-1)d]/2. Đây là công thức quan trọng giúp giải quyết nhiều bài toán thực tế liên quan đến tổng của dãy số.

Trong thực tế, cấp số cộng được ứng dụng rộng rãi trong nhiều lĩnh vực như tính lãi suất, tính lương tăng theo thâm niên, hay tính toán khoảng cách đều trong thiết kế. Ví dụ, một công ty quy định mức tăng lương hàng năm là 2 triệu đồng, với mức lương khởi điểm 10 triệu đồng, thì đây chính là một cấp số cộng với a₁ = 10 và d = 2.

Cách xác định công sai và số hạng tổng quát trong cấp số cộng

Để xác định chính xác các yếu tố trong một cấp số cộng, việc nắm vững công thức cấp số cộng là vô cùng quan trọng. Các yếu tố cốt lõi bao gồm công sai và số hạng tổng quát sẽ giúp giải quyết mọi bài toán liên quan đến dãy số này.

Việc tính toán các yếu tố trong cấp số cộng đòi hỏi sự chặt chẽ và tuân theo các quy tắc nhất định. Mỗi số hạng trong dãy số đều có mối liên hệ chặt chẽ với nhau thông qua một đại lượng không đổi.

Công thức tính công sai trong cấp số cộng được xác định bằng hiệu của hai số hạng liên tiếp bất kỳ trong dãy. Công sai thường được ký hiệu là d và có tính chất không đổi trong suốt dãy số.

Để tìm công sai, có thể lấy số hạng sau trừ đi số hạng trước: d = Un+1 – Un. Đây là đặc trưng quan trọng nhất của cấp số cộng, giúp phân biệt với các dãy số khác.

Công thức số hạng tổng quát Un = U1 + (n-1)d

Số hạng tổng quát của cấp số cộng được xác định thông qua công thức tính số số hạng với U1 là số hạng đầu tiên, n là số thứ tự của số hạng cần tìm và d là công sai.

Công thức này cho phép tìm được bất kỳ số hạng nào trong dãy mà không cần phải liệt kê tất cả các số hạng trước đó. Điều này đặc biệt hữu ích khi cần tìm số hạng ở vị trí xa.

Ví dụ minh họa cách tính số hạng tổng quát

Xét cấp số cộng có U1 = 3 và d = 2. Để tìm số hạng thứ 10, áp dụng công thức:
U10 = U1 + (10-1)d
U10 = 3 + 9×2 = 21

Tương tự, với cấp số cộng có U1 = -5 và d = 3:
U7 = -5 + (7-1)×3
U7 = -5 + 18 = 13

Các ví dụ trên minh họa cách áp dụng công thức một cách linh hoạt cho các trường hợp số hạng đầu và công sai khác nhau.

Phương pháp tính tổng n số hạng đầu tiên của cấp số cộng

Để tính được tổng n số hạng đầu tiên của một cấp số cộng, cần nắm vững các công thức tính công thức tính tổng cấp số cộng. Đây là phương pháp quan trọng giúp giải quyết nhiều bài toán trong thực tế.

Việc tính tổng cấp số cộng có thể thực hiện theo hai cách chính dựa vào số hạng đầu (U1) và số hạng cuối (Un) hoặc dựa vào số hạng đầu và công sai (d). Mỗi cách có ưu điểm riêng tùy thuộc vào dữ kiện của bài toán.

Công thức tính tổng Sn = n(U1 + Un)/2

Công thức này áp dụng khi biết được số hạng đầu U1 và số hạng cuối Un của dãy số. Ý nghĩa của công thức là lấy trung bình cộng của số hạng đầu và số hạng cuối, sau đó nhân với số lượng số hạng. Để tính cách tính trung bình cộng của U1 và Un, ta chỉ cần cộng chúng lại và chia 2.

Công thức này đặc biệt hữu ích khi số hạng cuối Un được cho trực tiếp, giúp tính toán nhanh chóng và chính xác mà không cần phải tìm công sai d.

Công thức tính tổng Sn = n[2U1 + (n-1)d]/2

Công thức thứ hai sử dụng số hạng đầu U1 và công sai d. Đây là công thức phổ biến khi bài toán cho biết công sai d thay vì số hạng cuối Un.

Biểu thức (n-1)d thể hiện tổng số lần cộng thêm công sai để đi từ số hạng đầu đến số hạng cuối. Nhân đôi số hạng đầu và cộng với tổng số lần tăng công sai sẽ cho kết quả chính xác.

Bài tập áp dụng công thức tính tổng

Áp dụng các công thức trên vào thực tế giải toán rất đa dạng. Ví dụ tính tổng các số tự nhiên từ 1 đến 100, ta có U1 = 1, Un = 100, n = 100. Thay vào công thức Sn = n(U1 + Un)/2 = 100(1 + 100)/2 = 5050.

Một ví dụ khác là tính tổng dãy số có U1 = 5, d = 3, n = 10. Áp dụng công thức Sn = n[2U1 + (n-1)d]/2 = 10[2×5 + (10-1)×3]/2 = 10(10 + 27)/2 = 185.

Việc thành thạo cả hai công thức giúp linh hoạt trong việc giải các dạng bài tập khác nhau, tùy thuộc vào dữ kiện được cho trong đề bài.

So sánh và phân biệt cấp số cộng với cấp số nhân

Công thức cấp số cộng cấp số nhân có những điểm khác biệt cơ bản về quy luật tạo thành dãy số. Cấp số cộng được tạo thành bằng cách cộng thêm một số cố định vào số hạng trước, trong khi cấp số nhân được tạo ra bằng cách nhân số hạng trước với một số cố định. Sự khác biệt này dẫn đến những đặc tính riêng biệt của mỗi loại dãy số.

Đặc điểm của cấp số cộng

Cấp số cộng có đặc điểm nổi bật là khoảng cách giữa các số hạng liên tiếp luôn không đổi. Điều này tạo nên một dãy số tăng hoặc giảm đều đặn theo một công sai d. Ví dụ trong dãy số 2, 5, 8, 11, 14, mỗi số hạng cách nhau một khoảng bằng 3 đơn vị.

Một đặc điểm quan trọng khác là tổng của hai số hạng cách đều số hạng giữa bằng hai lần số hạng giữa đó. Tính chất này giúp việc tính toán các số hạng trung gian trở nên dễ dàng hơn.

Đặc điểm của cấp số nhân

Cấp số nhân có tỷ số giữa hai số hạng liên tiếp luôn bằng một hằng số q gọi là công bội. Công thức tính công bội phụ thuộc vào số hạng đầu và số hạng thứ hai của dãy số. Đặc điểm này tạo ra sự tăng trưởng theo cấp số nhân, khiến các số hạng tăng hoặc giảm với tốc độ nhanh hơn so với cấp số cộng.

Tích của hai số hạng cách đều số hạng giữa bằng bình phương của số hạng giữa đó. Để tìm hiểu chi tiết hơn về quy luật này, bạn có thể tham khảo công thức cấp số nhân.

Các trường hợp đặc biệt

Trong thực tế, có những trường hợp đặc biệt khi công sai d của cấp số cộng bằng 0, dãy số sẽ trở thành dãy hằng số. Tương tự, khi công bội q của cấp số nhân bằng 1, dãy số cũng trở thành dãy hằng số.

Khi công bội q của cấp số nhân bằng -1, dãy số sẽ dao động qua lại giữa hai giá trị. Đây là hiện tượng không xuất hiện trong cấp số cộng và tạo nên tính đặc trưng riêng cho cấp số nhân.

Ngoài ra, cấp số nhân còn có trường hợp đặc biệt khi q = 0, khi đó tất cả các số hạng từ số hạng thứ hai trở đi đều bằng 0. Điều này tạo ra một dãy số rất đặc biệt không có trong cấp số cộng.

Ứng dụng công thức cấp số cộng trong giải toán

Công thức cấp số cộng được ứng dụng rộng rãi trong việc giải các bài toán về dãy số và tính tổng. Việc nắm vững và vận dụng linh hoạt các công thức sẽ giúp giải quyết hiệu quả nhiều dạng toán phức tạp, từ cơ bản đến nâng cao. Đặc biệt trong giải tích số, công thức này còn được sử dụng để tính gần đúng tích phân.

Bài toán tìm số hạng

Khi giải bài toán tìm số hạng trong cấp số cộng, việc xác định đúng số hạng đầu và công sai là bước quan trọng nhất. Thông thường, ta sẽ áp dụng công thức tổng quát an = a1 + (n-1)d, trong đó an là số hạng thứ n cần tìm, a1 là số hạng đầu tiên và d là công sai.

Một ví dụ điển hình là bài toán tìm số hạng thứ 100 của dãy số 2, 5, 8, 11,… Ta xác định được a1 = 2 và d = 3, từ đó dễ dàng tính được a100 = 2 + 99×3 = 299.

Bài toán tìm tổng

Trong các bài toán tìm tổng cấp số cộng, công thức Sn = n(a1 + an)/2 hoặc Sn = n[2a1 + (n-1)d]/2 thường được áp dụng. Việc chọn công thức phù hợp phụ thuộc vào dữ kiện đã cho trong đề bài.

Khi giải các bài toán phức tạp hơn, ta có thể kết hợp với các phương pháp khác như phương pháp đặt ẩn phụ hoặc phương pháp quy đổi về dạng cấp số cộng cơ bản.

Một số bài toán đòi hỏi phải tìm tổng các số hạng thỏa mãn điều kiện cho trước, khi đó cần xác định chính xác số lượng số hạng trước khi áp dụng công thức.

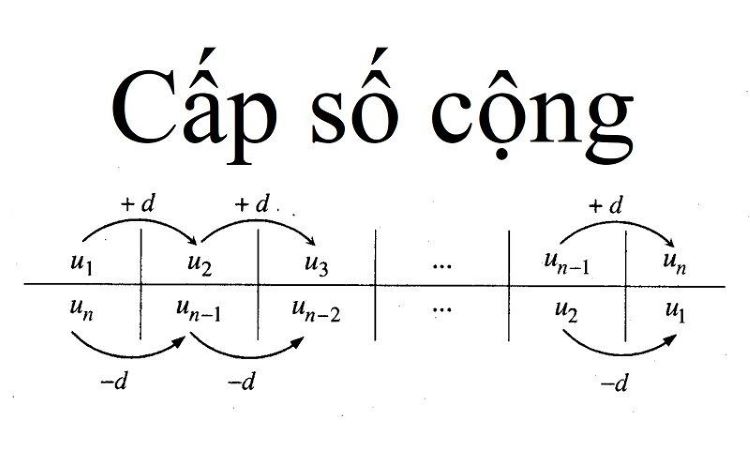
Bài toán thực tế

Theo nghiên cứu của Viện Khoa học Giáo dục Việt Nam, việc áp dụng cấp số cộng vào các tình huống thực tế giúp học sinh tiếp thu kiến thức tốt hơn 27% so với học thuần lý thuyết.

Một ứng dụng phổ biến là tính lương tăng theo thâm niên. Ví dụ, một công ty quy định mức lương khởi điểm 10 triệu đồng và tăng 500.000 đồng mỗi năm. Sau 5 năm, nhân viên có thể dễ dàng tính được tổng thu nhập của mình.

Trong lĩnh vực kinh tế, cấp số cộng còn được sử dụng để tính toán chi phí khấu hao tài sản cố định theo phương pháp đường thẳng, giúp doanh nghiệp hoạch định tài chính chính xác hơn.

Công thức cấp số cộng là một khái niệm quan trọng trong toán học, giúp chúng ta hiểu và tính toán dãy số hiệu quả. Bài viết đã đề cập đến công thức tính công sai, số hạng tổng quát, và các phương pháp tính tổng, từ đó giúp người đọc áp dụng vào bài toán một cách dễ dàng. Việc nắm vững các công thức này sẽ hỗ trợ bạn giải quyết các bài toán thực tiễn một cách hiệu quả.