Bảng phân phối Fisher luôn là những nội dung khó tiếp cận nhất trong môn học xác suất thống kê. Nội dung này không chỉ sở hữu khối lượng kiến thức khổng lồ, mà những kiến thức mới mẻ môn học này mang lại cũng gây không ít khó khăn cho các sinh viên.. Bài viết dưới đây chúng tôi sẽ cung cấp kiến thức đầy đủ nhất về nội dung này.
Bảng phân phối Fisher là gì?
Bảng phân phối Fisher, hay còn gọi là phân phối F, là một bảng thống kê được sử dụng trong kiểm định giả thuyết để xác định xem có sự khác biệt thống kê nào giữa hai phương sai mẫu hay không. Bảng này cho ta biết xác suất quan sát một giá trị F nhất định hoặc lớn hơn, giả sử không có sự khác biệt thực sự giữa hai phương sai.
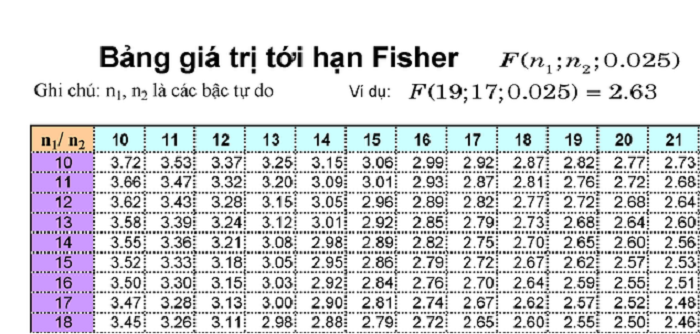
Phân phối Fisher thường được ký hiệu là F và phụ thuộc vào hai tham số: bậc tự do của tử số và bậc tự do của mẫu số. Nó đóng vai trò quan trọng trong việc so sánh phương sai giữa các nhóm và đánh giá mức độ phù hợp của mô hình thống kê. Các nhà nghiên cứu và phân tích dữ liệu thường sử dụng bảng phân phối Fisher để xác định giá trị tới hạn và tính toán p-value trong quá trình kiểm định giả thuyết.
Hàm mật độ và các tham số đặc trưng của F
Khi tìm hiểu về bảng Fisher, hàm mật độ và các tham số đặc trưng là những nội dung bạn không nên bỏ qua.
Hàm mật độ
Hàm mật độ của phân phối F với d1 và d2 bậc tự do được biểu diễn bởi một công thức phức tạp, bao gồm hàm gamma và các tham số d1, d2. Công thức này thể hiện xác suất của biến ngẫu nhiên F tại mỗi điểm x.
Các tham số đặc trưng của F
Dưới đây là thông tin đầy đủ về các tham số đặc trưng của F:
- Kỳ vọng (Expected value): E(F) = d1 / (d2 – 2), với điều kiện d2 > 2. Kỳ vọng này chỉ tồn tại khi d2 lớn hơn 2.
- Phương sai (Variance): Var(F) = [2d2^2 * (d1 + d2 – 2)] / [d1 * (d2 – 2)^2 * (d2 – 4)], với điều kiện d2 > 4. Phương sai chỉ tồn tại khi d2 lớn hơn 4.
- Mode (Giá trị có xác suất cao nhất): Mode = [(d1 – 2) * d2] / [d1 * (d2 + 2)], khi d1 > 2. Median (Trung vị): Không có công thức chính xác cho trung vị, nhưng có thể tính gần đúng bằng các phương pháp số.
Các tham số d1 và d2 là bậc tự do của tử số và mẫu số. Chúng ảnh hưởng đáng kể đến hình dạng của phân phối. Khi d1 và d2 tăng, phân phối Fisher sẽ tiệm cận đến phân phối chuẩn. Phân phối F luôn không âm và có độ lệch dương. Hình dạng của nó thường không đối xứng, nhưng sẽ trở nên gần đối xứng hơn khi các bậc tự do tăng lên.
Cách tra bảng phân phối Fisher đơn giản, chi tiết
Bước đầu tiên để tra bảng Fisher là xác định mức ý nghĩa α (thường là 0.05 hoặc 0.01) và hai bậc tự do: d1 (bậc tự do của tử số) và d2 (bậc tự do của mẫu số). Tiếp theo, tìm bảng phân phối Fisher phù hợp với mức ý nghĩa α đã chọn. Trong bảng, các cột thường biểu thị d1, còn các hàng biểu thị d2.
Để tra giá trị từ bảng tra Fisher, định vị cột tương ứng với d1 và hàng tương ứng với d2. Giao điểm của cột và hàng này chính là giá trị tới hạn F cần tìm. Nếu không tìm thấy chính xác giá trị d1 hoặc d2 trong bảng, có thể sử dụng phương pháp nội suy tuyến tính để ước tính giá trị gần đúng.
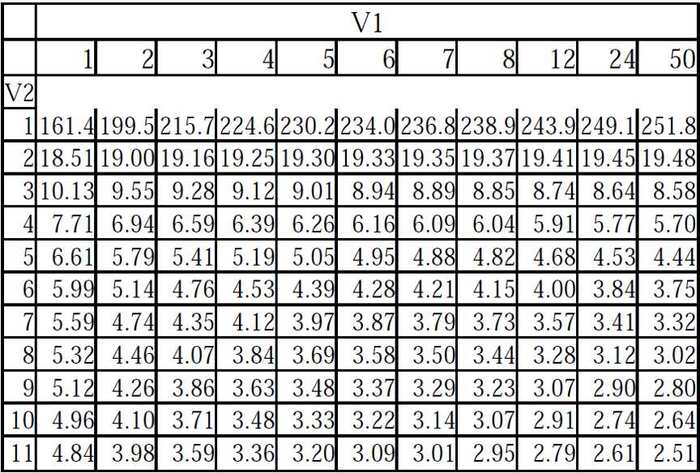
Cần lưu ý rằng một số bảng có thể được tổ chức khác nhau, ví dụ như d2 ở cột và d1 ở hàng. Trong trường hợp này, cách tra cứu sẽ được điều chỉnh tương ứng. Ngoài ra, với sự phát triển của công nghệ, nhiều phần mềm thống kê và máy tính khoa học ngày nay có thể tính toán giá trị F một cách chính xác mà không cần tra bảng phân phối F thủ công.
Ứng dụng của bảng phân phối Fisher
Bên cạnh, cách tra bảng Fisher, những thông tin về ứng dụng của bảng phân phối này cũng thu hút mối quan tâm của không ít người.
Phân tích phương sai
Phân tích phương sai (ANOVA) là một trong những ứng dụng quan trọng nhất của bảng phân phối Fisher. Trong ANOVA, phân phối F được sử dụng để so sánh sự biến thiên giữa các nhóm với sự biến thiên trong các nhóm. Điều này cho phép các nhà nghiên cứu xác định xem có sự khác biệt đáng kể giữa các nhóm hay không.
Kiểm định tỷ số phương sai
Kiểm định tỷ số phương sai là một ứng dụng khác của bảng phân phối Fisher. Phương pháp này cho phép các nhà thống kê so sánh độ biến thiên của hai tập dữ liệu độc lập. Điều này đặc biệt hữu ích trong việc đánh giá độ đồng nhất của phương sai, một giả định quan trọng trong nhiều phân tích thống kê.
Đánh giá ý nghĩa tổng thể mô hình
Trong hồi quy tuyến tính, bảng phân phối Fisher được sử dụng để đánh giá ý nghĩa tổng thể của mô hình thông qua kiểm định F. Kiểm định này so sánh mô hình hồi quy đầy đủ với một mô hình “null” chỉ có hệ số chặn. Nếu kiểm định F cho kết quả có ý nghĩa thống kê, điều này chỉ ra rằng mô hình hồi quy tốt hơn đáng kể so với việc chỉ sử dụng giá trị trung bình để dự đoán biến phụ thuộc.
Lời kết
Nhìn chung, thông qua bài viết trên hẳn bạn đã có cái nhìn đầy đủ nhất về bảng phân phối Fisher. Bên cạnh đó, chúng tôi cũng cung cấp cho bạn cách tra thông tin từ bảng và những ứng dụng thực tiễn mà nó mang lại để phục vụ cho quá trình học tập, nghiên cứu của bạn.