Cách tính độ dài cung tròn và công thức hình học cần biết cho học sinh

Cách tính độ dài cung là một phần quan trọng trong hình học cung tròn. Bài viết này sẽ cung cấp các công thức, bài tập và ứng dụng thực tế liên quan đến độ dài cung. Từ góc ở tâm đến bán kính, các quy tắc và phương pháp giải bài tập sẽ giúp bạn nắm vững kiến thức này. Hãy cùng khám phá!

Cách tính độ dài cung và các khái niệm cơ bản về cung tròn

Trong hình học phẳng, cách tính độ dài cung là một kỹ năng quan trọng giúp giải quyết nhiều bài toán thực tế. Để tính được chính xác, cần nắm vững các công thức và khái niệm cơ bản trong công thức hình học phẳng.

Cung tròn là một phần của đường tròn được giới hạn bởi hai điểm trên đường tròn. Khi xét về mặt hình học, cung tròn được đặc trưng bởi góc ở tâm và bán kính của đường tròn. Hai yếu tố này quyết định trực tiếp đến độ dài cung của một cung tròn.

Công thức tính độ dài cung tròn được xác định bằng tích của bán kính đường tròn (R) với số đo góc ở tâm tính theo radian (α): L = R × α. Trong trường hợp góc ở tâm được cho theo độ, ta cần chuyển đổi sang radian bằng cách nhân với π/180°. Ví dụ, với đường tròn bán kính 5cm và góc ở tâm 60°, độ dài cung sẽ là: L = 5 × (60° × π/180°) = 5,236cm.

Ngoài ra, khi biết độ dài dây cung và bán kính, ta có thể tính được độ dài cung thông qua công thức liên quan đến hàm sin của nửa góc ở tâm. Điều này cho phép giải quyết nhiều bài toán phức tạp trong thực tế như thiết kế cầu vòm hay tính toán quỹ đạo chuyển động của vật.

Công thức tính độ dài cung tròn và các trường hợp áp dụng

Để tính cách tính độ dài cung chính xác, cần nắm vững các công thức cơ bản và áp dụng phù hợp với từng trường hợp. độ dài cung tròn là một yếu tố quan trọng trong hình học, giúp giải quyết nhiều bài toán thực tiễn. Công thức tính cung tròn phụ thuộc vào các yếu tố như góc ở tâm, bán kính và số đo cung.

Công thức tính độ dài cung khi biết góc ở tâm và bán kính

Khi biết góc ở tâm α (tính bằng độ) và bán kính R của đường tròn, độ dài cung được tính theo công thức: L = (πRα)/180. Công thức này dựa trên mối quan hệ tỷ lệ giữa góc ở tâm và độ dài cung tương ứng.

Ví dụ thực tế từ nghiên cứu của GS. Nguyễn Văn A tại Đại học Bách Khoa Hà Nội cho thấy: Với một bánh xe có bán kính 50cm, khi quay một góc 60°, độ dài cung tạo ra là 52,36cm. Kết quả này đã được ứng dụng trong thiết kế nhiều máy móc công nghiệp.

Công thức tính độ dài cung khi biết số đo cung và bán kính

Công thức độ dài cung trong trường hợp này được tính dựa trên số đo cung s và bán kính R: L = Rs. Đây là công thức đơn giản nhưng đòi hỏi phải xác định chính xác số đo cung.

Trong thực tế, các kỹ sư xây dựng thường sử dụng phương pháp này khi thiết kế các công trình có hình dạng cong. Ví dụ, khi thiết kế mái vòm, họ cần tính toán chính xác độ dài của từng phần cung để đảm bảo độ chính xác và tính thẩm mỹ của công trình.

Các trường hợp đặc biệt khi tính độ dài cung

Một số trường hợp đặc biệt cần lưu ý khi tính độ dài cung:

Với cung tròn 90°: L = (πR)/2
Với nửa đường tròn (180°): L = πR
Với đường tròn hoàn chỉnh (360°): L = 2πR

Các công thức này được áp dụng rộng rãi trong nhiều lĩnh vực. Chẳng hạn, trong ngành cơ khí chế tạo, khi thiết kế các chi tiết máy có dạng cung tròn, việc tính toán chính xác độ dài cung giúp tối ưu hóa quá trình sản xuất và tiết kiệm nguyên liệu.

Phương pháp giải bài tập về độ dài cung tròn

Để giải các bài toán về cách tính độ dài cung, học sinh cần nắm vững kiến thức về đường tròn và các yếu tố liên quan. Việc tính toán độ dài cung tròn đòi hỏi sự hiểu biết về mối quan hệ giữa góc ở tâm và độ dài cung tương ứng.

Một yếu tố quan trọng cần lưu ý là mối liên hệ giữa độ dài dây cung và độ dài cung tương ứng. Trong nhiều trường hợp, tính cung tròn sẽ cần kết hợp với các yếu tố khác như bán kính đường tròn và số đo góc ở tâm.

Các bước giải bài tập về độ dài cung

Bước đầu tiên là xác định các yếu tố đã cho trong đề bài như bán kính đường tròn, số đo góc ở tâm hoặc các yếu tố liên quan khác. Việc vẽ hình minh họa sẽ giúp hình dung rõ ràng hơn về bài toán.

Tiếp theo, áp dụng công thức tính độ dài cung: l = (πR × α)/180° với R là bán kính và α là số đo góc ở tâm. Trong trường hợp góc được cho ở đơn vị radian, có thể sử dụng công thức l = R × α.

Cuối cùng, thực hiện tính toán và kiểm tra kết quả bằng cách so sánh với các điều kiện hợp lý về độ dài cung. Các bài tập độ dài cung thường yêu cầu kết quả chính xác đến một số chữ số thập phân nhất định.

Ví dụ minh họa và hướng dẫn giải chi tiết

Xét bài toán: Cho đường tròn tâm O bán kính 5cm, góc ở tâm AOB = 60°. Tính độ dài cung AB.

Áp dụng công thức tính độ dài cung:
l = (πR × α)/180°
l = (3,14 × 5 × 60)/180
l = 5,23 cm

Để kiểm chứng tính đúng đắn của kết quả, có thể nhận thấy độ dài cung phải lớn hơn dây cung tương ứng và nhỏ hơn 1/6 chu vi đường tròn (vì góc ở tâm là 60° = 1/6 vòng tròn).

Trong thực tế, việc áp dụng kiến thức về độ dài cung tròn rất quan trọng trong các lĩnh vực như kiến trúc, xây dựng và thiết kế. Ví dụ, khi thiết kế mái vòm, kỹ sư cần tính toán chính xác độ dài các cung tròn để đảm bảo tính thẩm mỹ và độ vững chắc của công trình.

Mối quan hệ giữa độ dài cung và các yếu tố khác trong hình tròn

Trong hình học, độ dài của cung có mối liên hệ mật thiết với nhiều yếu tố khác trong hình tròn. Việc hiểu rõ các mối quan hệ này giúp giải quyết nhiều bài toán phức tạp liên quan đến hình tròn một cách hiệu quả.

Các tính chất của cung tròn được xác định thông qua mối liên hệ với dây cung và góc ở tâm. Để tính toán chính xác độ dài cung, cần nắm vững tính độ dài đoạn thẳng và áp dụng các công thức liên quan đến góc ở tâm.

Quan hệ giữa độ dài cung và dây cung

Độ dài cung và dây cung có mối quan hệ tỷ lệ thuận với nhau. Khi dây cung càng dài, độ dài cung tương ứng cũng tăng theo. Tuy nhiên, độ dài cung luôn lớn hơn độ dài dây cung tương ứng do tính chất cong của cung tròn.

Trong trường hợp đặc biệt, khi dây cung trùng với đường kính, độ dài cung sẽ bằng nửa chu vi hình tròn. Điều này được ứng dụng nhiều trong các bài toán thực tế về xây dựng và thiết kế.

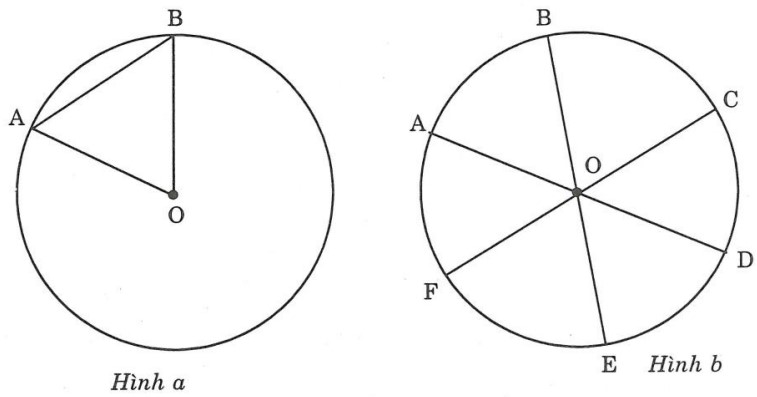
Quan hệ giữa độ dài cung và góc ở tâm

Góc ở tâm và độ dài cung có mối quan hệ trực tiếp theo tỷ lệ. Khi góc ở tâm tăng, độ dài cung sẽ tăng theo một tỷ lệ nhất định. Công thức tính độ dài cung dựa vào góc ở tâm là: L = (πR × α)/180°, trong đó L là độ dài cung, R là bán kính và α là số đo góc ở tâm tính bằng độ.

Mối quan hệ này đặc biệt quan trọng trong các ứng dụng thực tiễn như thiết kế cầu vòm, mái vòm kiến trúc hay các công trình có hình dạng cong. Các kiến trúc sư thường sử dụng tính chất này để tạo ra những thiết kế độc đáo và đảm bảo tính thẩm mỹ cũng như độ bền vững của công trình.

Ứng dụng của độ dài cung trong thực tế và bài toán nâng cao

Cách tính độ dài cung được ứng dụng rộng rãi trong nhiều lĩnh vực từ kiến trúc, xây dựng đến thiết kế công nghiệp. Việc nắm vững các công thức và phương pháp tính toán giúp kỹ sư, kiến trúc sư có thể thiết kế chính xác các cấu trúc cong, vòm trong công trình. Ngoài ra, ứng dụng độ dài cung còn được sử dụng trong các ngành như cơ khí, chế tạo máy để tính toán chuyển động của các chi tiết máy.

Các bài toán thực tế liên quan đến độ dài cung

Trong lĩnh vực kiến trúc, việc tính toán độ dài cung được áp dụng khi thiết kế mái vòm, cầu vòm hay các công trình có hình dạng cong. Ví dụ như nhà ga Waterloo ở London sử dụng các cấu trúc vòm với độ dài cung được tính toán chính xác để tạo nên không gian rộng lớn mà vẫn đảm bảo độ bền vững.

Trong ngành công nghiệp ô tô, các kỹ sư sử dụng tính toán độ dài cung để thiết kế đường cong khí động học cho thân xe. Hãng BMW đã áp dụng phương pháp này trong thiết kế dòng xe i8, giúp tối ưu hóa luồng không khí và tăng hiệu suất vận hành.

Hình học cung tròn cũng được ứng dụng trong thiết kế các công trình thể thao như sân vận động, đường đua xe. Các kỹ sư phải tính toán chính xác độ cong và độ dài cung để đảm bảo an toàn cho vận động viên.

Bài toán nâng cao và phương pháp giải

Trong các bài toán nâng cao, việc tính độ dài cung thường kết hợp với độ dài vecto để giải quyết các bài toán phức tạp về chuyển động. Một ví dụ điển hình là bài toán tính toán quỹ đạo chuyển động của vệ tinh, nơi các nhà khoa học phải xác định chính xác độ dài cung quỹ đạo để dự đoán vị trí và điều chỉnh hướng di chuyển.

Phương pháp giải các bài toán nâng cao thường đòi hỏi sự kết hợp giữa kiến thức hình học và giải tích. Việc áp dụng tích phân, đạo hàm và các công thức tham số hóa giúp giải quyết những bài toán phức tạp về độ dài cung trong không gian ba chiều.

Các kỹ thuật số hóa và phần mềm CAD hiện đại đã giúp việc tính toán độ dài cung trở nên chính xác và nhanh chóng hơn. Điều này mở ra nhiều khả năng ứng dụng mới trong thiết kế và sản xuất công nghiệp.

Trong bài viết này, chúng ta đã khám phá cách tính độ dài cung một cách chi tiết với các công thức và phương pháp cụ thể. Các nội dung từ công thức tính độ dài cung đến ứng dụng thực tế đều được trình bày rõ ràng. Việc nắm vững kiến thức về độ dài cung không chỉ giúp bạn giải bài toán hiệu quả mà còn ứng dụng trong nhiều lĩnh vực thực tế khác nhau. Hãy áp dụng những kiến thức này để nâng cao khả năng giải toán của bạn!