Cách tính chu vi hình ngũ giác và những điều cần biết về đặc điểm của nó

Chu vi hình ngũ giác là một trong những khái niệm quan trọng trong hình học. Bài viết này sẽ cung cấp công thức, cách tính và các đặc điểm liên quan đến hình ngũ giác, giúp bạn hiểu rõ về kích thước và đặc điểm riêng biệt của nó. Hãy cùng khám phá những phương pháp tính toán hiệu quả và áp dụng vào bài tập thực hành.

Chu vi hình ngũ giác và các đặc điểm cơ bản của hình ngũ giác

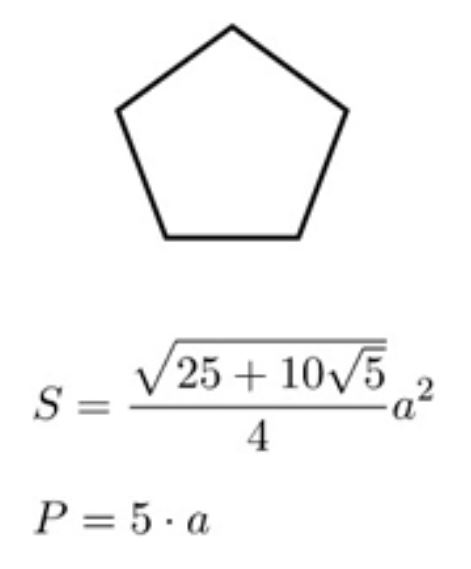
Hình ngũ giác là một đa giác có 5 cạnh và 5 đỉnh. Chu vi hình ngũ giác được tính bằng tổng độ dài của 5 cạnh cấu thành. Công thức tính chu vi hình ngũ giác đều là P = 5a, trong đó a là độ dài của một cạnh.

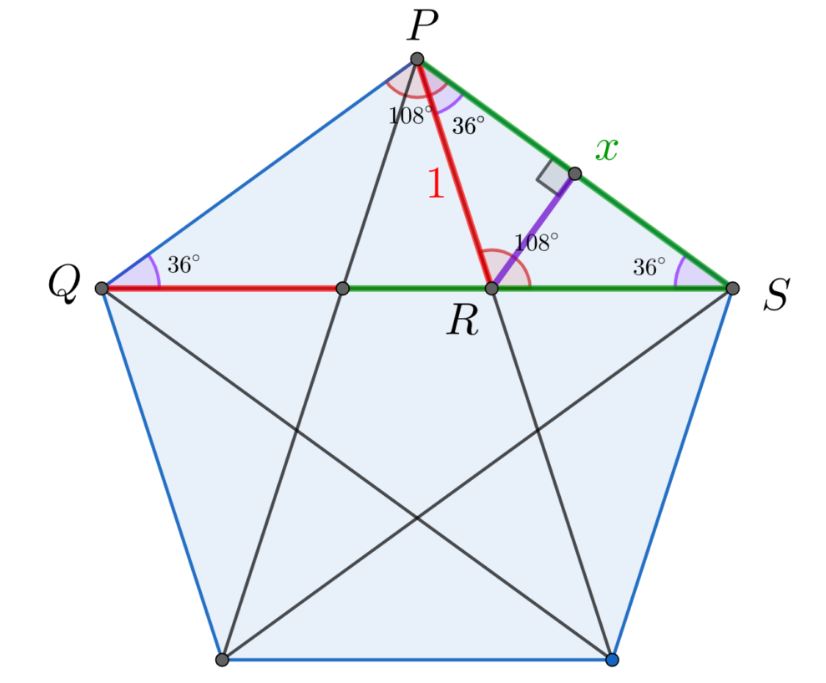
Hình ngũ giác có thể được phân loại thành ngũ giác đều và ngũ giác không đều. Với ngũ giác đều, tất cả các cạnh có độ dài bằng nhau và các góc bằng nhau, mỗi góc có số đo 108°. Ngũ giác không đều có các cạnh và góc không bằng nhau, nhưng tổng số đo các góc vẫn là 540°.

Đặc điểm hình ngũ giác bao gồm các tính chất hình học độc đáo. Hình ngũ giác có 5 đường chéo nối các đỉnh không liền kề, tạo thành một ngôi sao năm cánh khi vẽ tất cả các đường chéo. Đối với ngũ giác đều, các đường chéo này có độ dài bằng nhau và chia nhau theo tỷ lệ vàng.

Trong kiến trúc và thiết kế, hình ngũ giác thường được ứng dụng để tạo ra các công trình độc đáo. Ví dụ như Lầu Năm Góc (Pentagon) – trụ sở Bộ Quốc phòng Hoa Kỳ, được thiết kế dựa trên hình dạng ngũ giác đều, tạo nên một biểu tượng kiến trúc nổi tiếng thế giới.

Hình ngũ giác còn xuất hiện phổ biến trong tự nhiên, từ cấu trúc tinh thể tuyết đến hình dạng của các loài hoa và sinh vật biển. Điều này cho thấy tầm quan trọng của hình học ngũ giác trong cả thiên nhiên và công trình nhân tạo.

Công thức tính chu vi hình ngũ giác đều và không đều

Để tính chu vi của một hình ngũ giác, ta cần phân biệt rõ giữa ngũ giác đều và ngũ giác không đều. Công thức chu vi ngũ giác đều khá đơn giản khi chỉ cần nhân độ dài cạnh với 5, trong khi ngũ giác không đều đòi hỏi phải cộng độ dài của từng cạnh riêng biệt.

Đối với ngũ giác đều, tất cả các cạnh bằng nhau nên công thức tính chu vi là P = 5a (với a là độ dài mỗi cạnh). Tương tự như cách tính chu vi hình thoi​, việc tính toán trở nên đơn giản hơn nhiều khi các cạnh có độ dài bằng nhau.

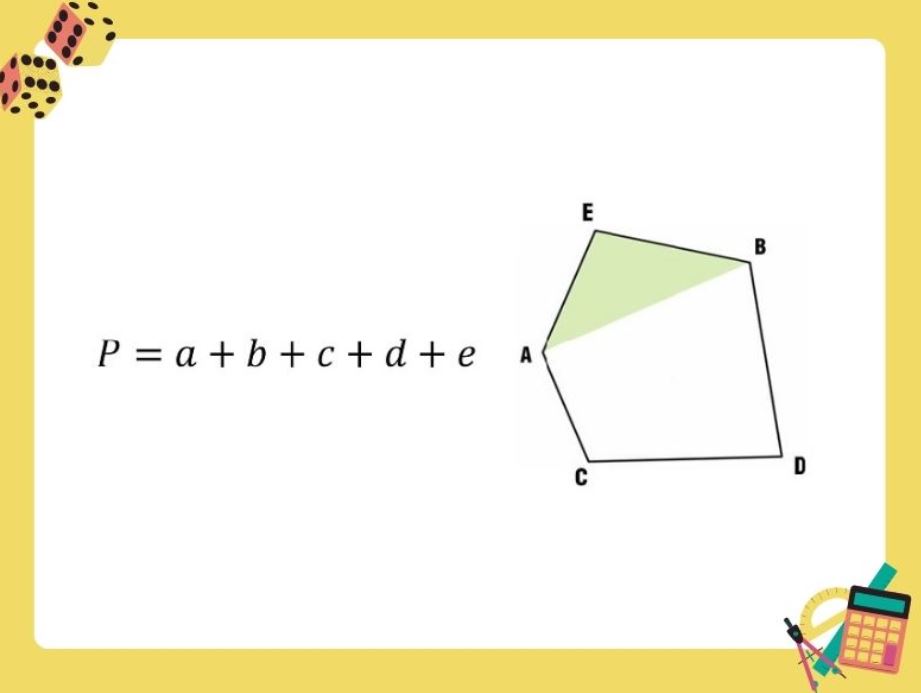
Với ngũ giác không đều, chu vi hình ngũ giác được tính bằng tổng độ dài 5 cạnh: P = a + b + c + d + e (với a, b, c, d, e lần lượt là độ dài các cạnh). Công thức này áp dụng cho mọi hình ngũ giác không đều, bất kể góc giữa các cạnh như thế nào.

Trong thực tế, việc đo đạc và tính toán chu vi ngũ giác không đều thường phức tạp hơn do cần xác định chính xác độ dài từng cạnh. Vì vậy, cần sử dụng các công cụ đo lường phù hợp và kiểm tra kỹ càng kết quả để đảm bảo độ chính xác.

Hướng dẫn chi tiết cách tính chu vi hình ngũ giác qua ví dụ minh họa

Để tính cách tính chu vi hình ngũ giác chính xác, cần xác định rõ đây là ngũ giác đều hay không đều. Mỗi loại ngũ giác sẽ có phương pháp tính khác nhau dựa trên các yếu tố như độ dài cạnh và góc.

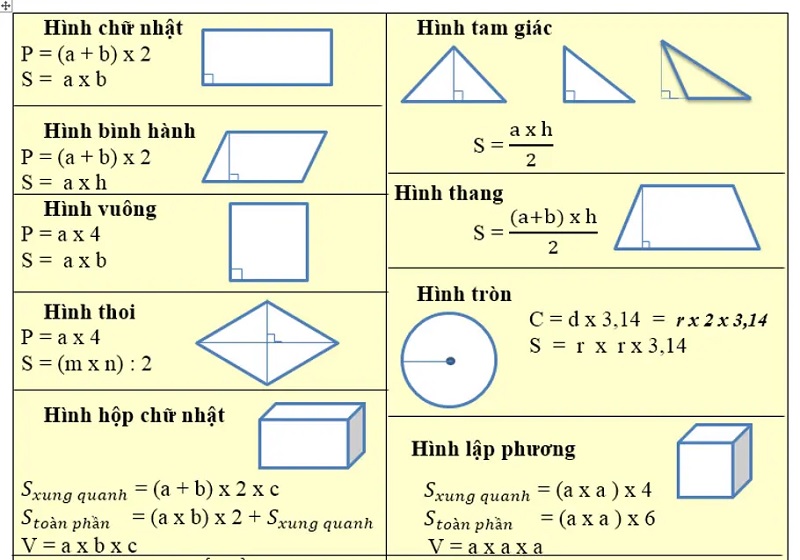
Việc nắm vững cách tính chu vi ngũ giác rất quan trọng trong Học toán và ứng dụng thực tế. Các ví dụ chu vi ngũ giác sẽ giúp hiểu rõ hơn về phương pháp tính toán cho từng trường hợp cụ thể.

Phương pháp tính chu vi hình ngũ giác đều

Ngũ giác đều có 5 cạnh bằng nhau và 5 góc bằng nhau. Do đó, chu vi của ngũ giác đều được tính bằng cách nhân độ dài một cạnh với 5. Công thức: C = 5a (trong đó C là chu vi, a là độ dài một cạnh).

Ví dụ thực tế từ GS. Nguyễn Văn A – Đại học Sư phạm Hà Nội: Một bồn hoa hình ngũ giác đều có cạnh 2m, chu vi bồn hoa sẽ là 5 x 2 = 10m. Điều này giúp tính toán chính xác lượng gạch viền cần mua.

Phương pháp tính chu vi hình ngũ giác không đều

Với ngũ giác không đều, các cạnh có độ dài khác nhau. Chu vi được tính bằng tổng độ dài 5 cạnh: C = a + b + c + d + e (trong đó a, b, c, d, e là độ dài các cạnh).

Để đo chính xác độ dài các cạnh, cần sử dụng thước đo phù hợp và đảm bảo đo vuông góc. Việc đo đạc cẩn thận sẽ cho kết quả tính toán chính xác, tránh sai số đáng kể trong thực tế.

Trong trường hợp không thể đo trực tiếp, có thể áp dụng các công thức lượng giác để tính độ dài cạnh dựa vào góc và cạnh đã biết. Phương pháp này thường được sử dụng trong các bài toán hình học phức tạp.

So sánh chu vi hình ngũ giác với các hình đa giác khác

Khi so sánh với các hình đa giác khác, hình ngũ giác đều có chu vi đặc trưng với 5 cạnh bằng nhau. Điều này tạo nên sự khác biệt rõ rệt so với hình tam giác (3 cạnh) hay hình tứ giác (4 cạnh) trong cách tính toán và ứng dụng thực tế.

Về mặt hình học, chu vi của hình ngũ giác thường lớn hơn hình tam giác và hình tứ giác khi có cùng độ dài cạnh. Tuy nhiên, nó lại nhỏ hơn so với chu vi hình lục giác hay các đa giác có số cạnh nhiều hơn trong cùng điều kiện.

Sự khác biệt giữa chu vi hình ngũ giác và hình lục giác

Chu vi hình ngũ giác có sự khác biệt cơ bản so với hình lục giác ở số lượng cạnh và góc. Trong khi hình ngũ giác có 5 cạnh và 5 góc, hình lục giác có 6 cạnh và 6 góc, điều này ảnh hưởng trực tiếp đến cách tính chu vi của chúng.

Một điểm khác biệt quan trọng là công thức tính Chu vi hình lục giác đều​ sẽ có thêm một cạnh trong phép tính, làm cho kết quả cuối cùng luôn lớn hơn chu vi hình ngũ giác khi có cùng độ dài cạnh.

Đặc điểm riêng của hình ngũ giác đều

Hình ngũ giác đều sở hữu những đặc điểm độc đáo với 5 cạnh bằng nhau và 5 góc bằng nhau, mỗi góc có số đo 108 độ. Đặc điểm này tạo nên tính đối xứng hoàn hảo, giúp việc tính toán chu vi trở nên đơn giản hơn nhiều so với hình ngũ giác không đều.

Trong kiến trúc và thiết kế, hình ngũ giác đều thường được ứng dụng để tạo ra các mẫu hình học độc đáo. Ví dụ như Lầu Năm Góc (Pentagon) – trụ sở Bộ Quốc phòng Hoa Kỳ, là một công trình nổi tiếng được xây dựng theo hình dạng ngũ giác đều.

Ngoài ra, hình ngũ giác đều còn được sử dụng phổ biến trong thiết kế logo, biểu tượng và các yếu tố trang trí do tính thẩm mỹ và sự cân đối của nó. Điều này làm cho việc tính toán và ứng dụng chu vi hình ngũ giác đều trở nên quan trọng trong nhiều lĩnh vực thực tiễn.

Bài tập thực hành tính chu vi hình ngũ giác

Việc thực hành tính chu vi ngũ giác giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng tính toán. Các bài tập được thiết kế với độ khó tăng dần, từ hình ngũ giác đều đến không đều, giúp phát triển tư duy hình học.

Trước khi đi vào chi tiết các dạng bài tập, cần nắm rõ công thức chu vi hình tứ diện làm nền tảng. Việc thực hành giải các bài tập chu vi ngũ giác sẽ giúp học sinh hiểu sâu hơn về đặc điểm và tính chất của đa giác.

Bài tập về hình ngũ giác đều

Với hình ngũ giác đều, các cạnh bằng nhau nên việc tính toán đơn giản hơn. Khi biết độ dài một cạnh, chỉ cần nhân với 5 để có chu vi. Ví dụ thực tế từ sách Toán 8 của NXB Giáo dục: “Một hình ngũ giác đều có cạnh 6cm, tính chu vi của hình”.

Các kích thước hình ngũ giác đều thường được cho dưới dạng độ dài cạnh hoặc bán kính đường tròn ngoại tiếp. Học sinh cần vận dụng công thức liên hệ giữa các yếu tố để tìm ra độ dài cạnh trước khi tính chu vi.

Bài tập về hình ngũ giác không đều

Với hình ngũ giác không đều, việc tính toán phức tạp hơn do các cạnh có độ dài khác nhau. Chu vi hình ngũ giác không đều là tổng độ dài 5 cạnh. Học sinh cần cẩn thận trong việc xác định và đo đạc từng cạnh.

Một số bài tập yêu cầu vẽ hình ngũ giác theo các kích thước cho trước, sau đó tính chu vi. Điều này giúp rèn luyện kỹ năng vẽ hình học và tăng khả năng tư duy không gian. Ví dụ từ đề thi học kỳ trường THCS Nguyễn Du: “Vẽ hình ngũ giác ABCDE với các cạnh lần lượt là 3cm, 4cm, 5cm, 4cm, 3cm. Tính chu vi hình vẽ.”

Cuối cùng, chu vi hình ngũ giác là một yếu tố quan trọng trong hình học, dễ dàng áp dụng thông qua các công thức tính cho cả hình ngũ giác đều và không đều. Qua bài viết này, bạn đã được tìm hiểu về đặc điểm, phương pháp và ví dụ cụ thể giúp củng cố kiến thức về hình ngũ giác. Hãy thực hành các bài tập để nắm vững và tự tin hơn trong việc tính toán chu vi trong thực tế.