Chu vi hình thoi là độ dài tổng các cạnh của hình thoi, một khái niệm quan trọng trong toán học. Tìm hiểu công thức tính chu vi hình thoi, cùng các ứng dụng thực tế và ví dụ minh họa để nắm chắc kiến thức này.
Chu vi hình thoi là độ dài tổng các cạnh của hình thoi
Hình thoi là hình gì là một tứ giác có 4 cạnh bằng nhau và các cạnh đối song song với nhau. Đây là một hình học phẳng có nhiều tính chất đặc biệt và được ứng dụng rộng rãi trong thực tế.
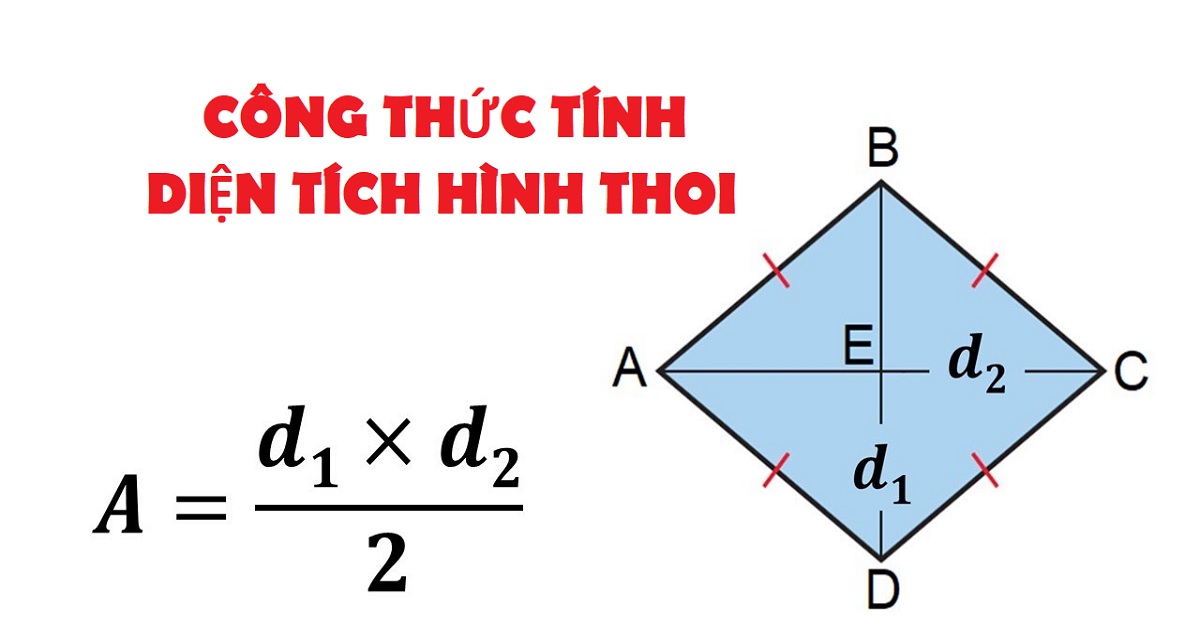
Chu vi hình thoi được tính bằng cách cộng độ dài của tất cả các cạnh lại với nhau. Do hình thoi có 4 cạnh bằng nhau nên chu vi sẽ bằng 4 lần độ dài một cạnh. Công thức tính chu vi hình thoi là P = 4a, trong đó a là độ dài cạnh của hình thoi.
Ví dụ, một hình thoi có độ dài mỗi cạnh là 5cm thì chu vi của hình thoi sẽ là: P = 4 × 5 = 20cm. Điều này cho thấy việc tính chu vi hình thoi khá đơn giản so với các hình tứ giác khác vì chỉ cần biết độ dài một cạnh là có thể tính được chu vi.
Đặc điểm và tính chất của hình thoi ảnh hưởng đến chu vi
Đặc điểm hình thoi là yếu tố quyết định trực tiếp đến cách tính và giá trị chu vi của hình. Các tính chất đặc trưng của hình thoi tạo nên sự khác biệt so với các hình tứ giác khác, đồng thời ảnh hưởng đến phương pháp xác định chu vi.
Để hiểu rõ mối liên hệ giữa đặc điểm và chu vi hình thoi, cần phân tích ba tính chất cơ bản sau đây. Những tính chất này không chỉ giúp nhận dạng hình thoi mà còn là cơ sở để tính toán các yếu tố liên quan.
Các cạnh bằng nhau là đặc trưng quan trọng của hình thoi
Tính chất quan trọng nhất của hình thoi là bốn cạnh có độ dài bằng nhau. Đặc điểm này khiến việc tính chu vi trở nên đơn giản hơn so với các hình tứ giác khác, chỉ cần nhân độ dài một cạnh với 4.
Khi xét về mặt hình học, tính chất cạnh bằng nhau tạo ra sự cân đối và đối xứng cho hình thoi. Điều này không chỉ ảnh hưởng đến tính thẩm mỹ mà còn tác động trực tiếp đến các phép tính liên quan đến chu vi và diện tích.
Các góc đối bằng nhau trong hình thoi
Trong hình thoi, các góc đối diện luôn bằng nhau và bổ túc cho nhau. Tổng số đo bốn góc của hình thoi luôn bằng 360 độ, với hai cặp góc đối bằng nhau tạo nên sự cân đối hoàn hảo.
Tính chất này có ý nghĩa quan trọng trong việc xác định hướng và độ nghiêng của đường chéo hình thoi. Khi hai góc đối bằng nhau, các đường chéo sẽ chia hình thoi thành các tam giác cân bằng nhau.
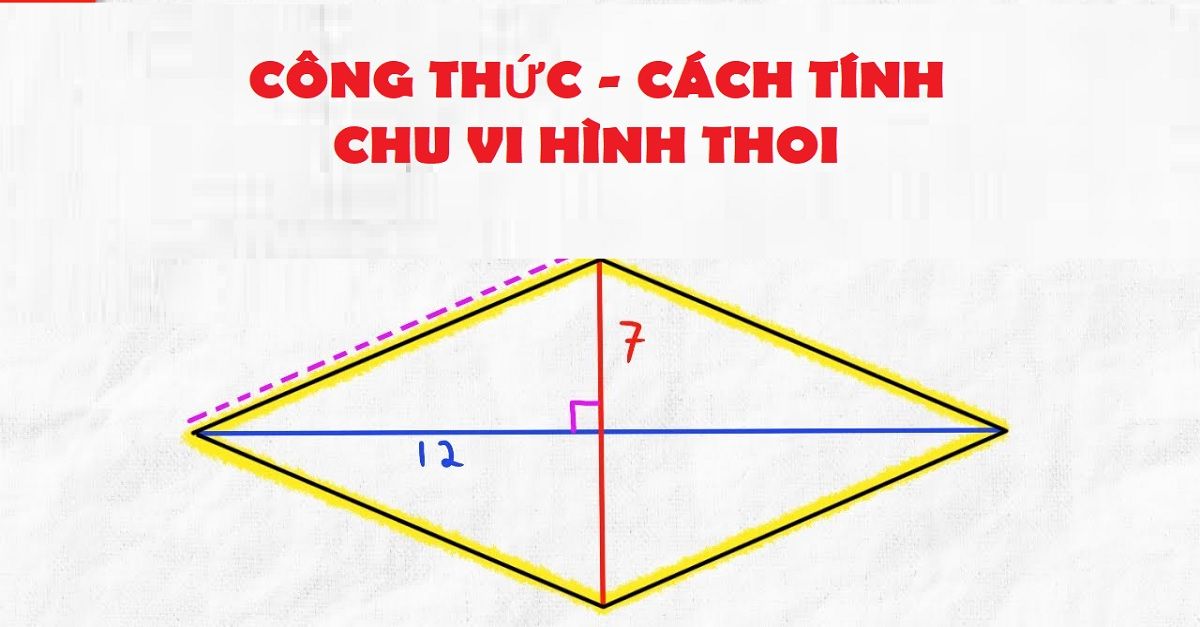
Đặc điểm góc đối bằng nhau còn giúp phân biệt hình thoi với các hình tứ giác khác, đồng thời tạo điều kiện thuận lợi cho việc tính toán các yếu tố hình học khác.
Hai đường chéo vuông góc và cắt đôi nhau
Hai đường chéo của hình thoi luôn vuông góc và cắt đôi lẫn nhau tại trung điểm. Tính chất này tạo ra bốn tam giác vuông bằng nhau khi kẻ đường chéo.
Đặc điểm này có vai trò quan trọng trong việc tính diện tích hình thoi, bởi diện tích được xác định bằng tích của hai đường chéo chia 2. Sự vuông góc của đường chéo cũng tạo điều kiện thuận lợi cho việc áp dụng định lý Pytago trong các bài toán phức tạp.
Tính chất đường chéo vuông góc và cắt đôi nhau còn giúp xác định tâm đối xứng của hình thoi, từ đó làm cơ sở cho nhiều phép biến hình hình học khác nhau.
Công thức tính chu vi hình thoi và cách áp dụng
Để tính được chu vi của một hình thoi, ta cần nắm rõ công thức tính chu vi hình thoi và các bước thực hiện cụ thể. Hình thoi là một tứ giác đặc biệt với 4 cạnh bằng nhau, do đó việc tính toán chu vi sẽ đơn giản hơn so với các hình tứ giác khác.
Công thức cơ bản P = 4a (với a là độ dài cạnh)
kí hiệu chu vi của hình thoi được tính bằng tổng độ dài 4 cạnh. Do các cạnh của hình thoi bằng nhau nên ta chỉ cần nhân độ dài một cạnh với 4. Công thức này áp dụng cho mọi hình thoi, không phụ thuộc vào độ lớn của các góc.
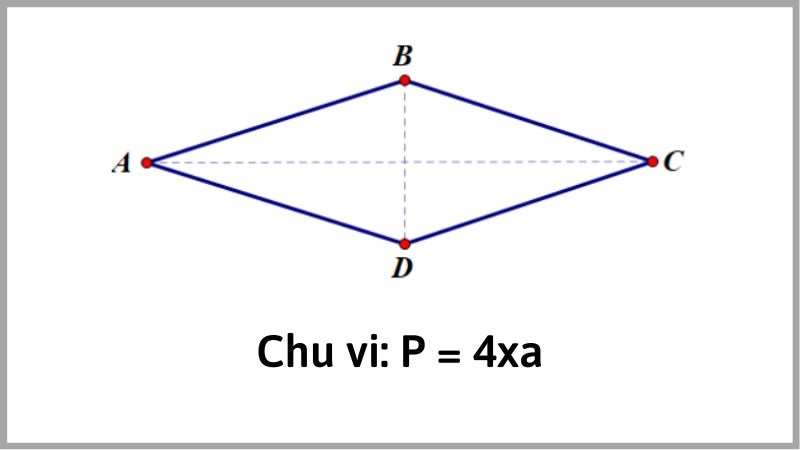
Ví dụ thực tế từ GS. Nguyễn Văn An – Đại học Sư phạm Hà Nội: “Khi tính chu vi hình thoi, sinh viên thường nhầm lẫn với diện tích. Điều quan trọng là nhớ rằng chu vi chỉ phụ thuộc vào độ dài cạnh, không liên quan đến độ dài đường chéo.”
Các bước tính chu vi hình thoi
Cách tính chu vi hình thoi được thực hiện qua hai bước chính. Mỗi bước đều quan trọng và cần được thực hiện chính xác để có kết quả đúng.
Xác định độ dài cạnh
Đo độ dài một cạnh của hình thoi bằng thước hoặc dựa vào dữ kiện cho sẵn trong bài toán. Việc đo đạc cần thực hiện cẩn thận và chính xác đến đơn vị đo lường nhỏ nhất có thể.
Trong trường hợp không thể đo trực tiếp, có thể sử dụng các định lý toán học như Pytago hoặc công thức lượng giác để tính độ dài cạnh từ các yếu tố khác được cho.
Áp dụng công thức tính
Sau khi có độ dài cạnh, nhân con số này với 4 để được chu vi. Kết quả cần ghi rõ đơn vị đo lường phù hợp. Nếu bài toán yêu cầu làm tròn số, cần tuân thủ số chữ số thập phân theo yêu cầu.
Kiểm tra lại kết quả bằng cách ước lượng để đảm bảo tính hợp lý của đáp số. Một hình thoi có cạnh 5cm sẽ có chu vi là 20cm – con số này cần phải phù hợp với kích thước thực tế của hình vẽ.
Ví dụ minh họa cách tính chu vi hình thoi
Để giúp hiểu rõ hơn về ví dụ chu vi hình thoi, chúng ta sẽ phân tích một số bài toán điển hình. Mỗi bài toán sẽ minh họa các phương pháp khác nhau để tính chu vi hình thoi dựa trên các yếu tố đã biết.
Bài toán với độ dài cạnh cho trước
Một hình thoi có độ dài cạnh là 6cm. Đây là trường hợp đơn giản nhất để tính chu vi, chỉ cần nhân độ dài cạnh với 4. Kết quả chu vi sẽ là 24cm.
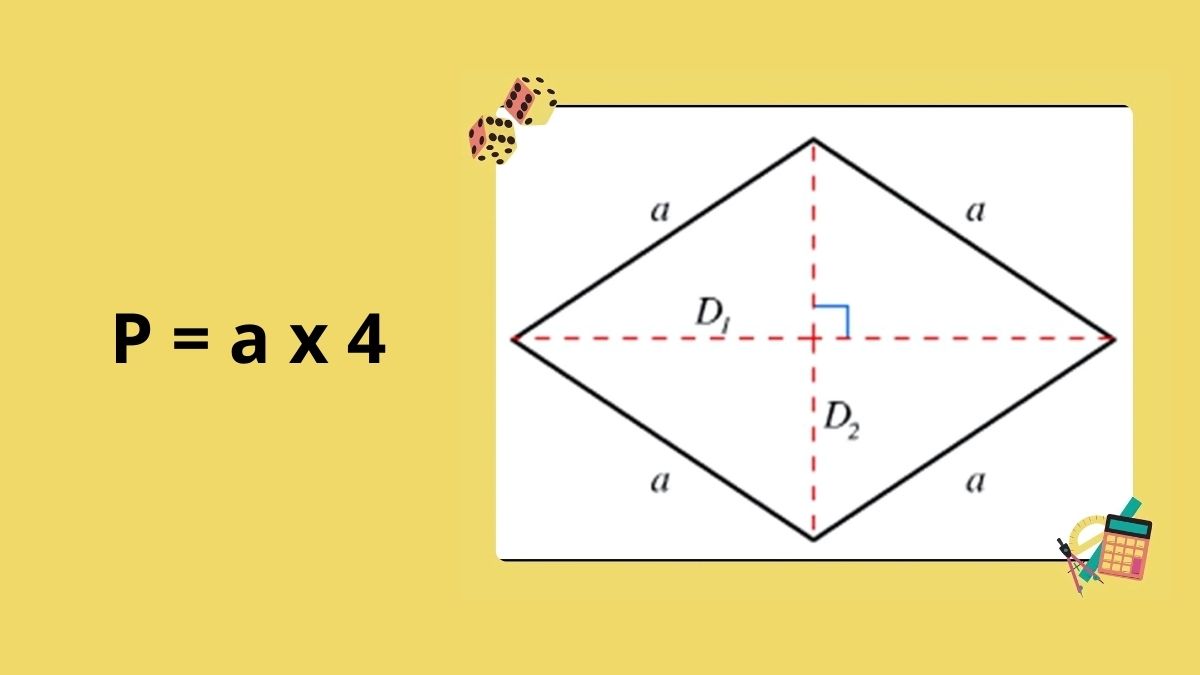
Tương tự, khi một hình thoi có cạnh 8,5cm, chu vi sẽ là 34cm. Điều này cho thấy công thức tính chu vi hình thoi chỉ phụ thuộc vào độ dài cạnh, không liên quan đến các yếu tố khác như góc hay đường chéo.
Bài toán tìm chu vi từ đường chéo
Khi biết hai đường chéo của hình thoi lần lượt là 8cm và 6cm, ta cần áp dụng định lý Pytago để tìm độ dài cạnh. Nửa đường chéo lớn là 4cm và nửa đường chéo nhỏ là 3cm sẽ tạo thành tam giác vuông với cạnh huyền chính là cạnh hình thoi.
Áp dụng công thức tính cạnh huyền: a = √(4² + 3²) = 5cm. Do đó chu vi hình thoi sẽ là 20cm. Để tìm hiểu thêm về các phép tính liên quan đến hình thoi, bạn có thể tham khảo cách tính diện tích hình thoi.
Bài toán phức tạp hơn liên quan đến chu vi hình thoi
Một hình thoi có đường chéo lớn gấp đôi đường chéo nhỏ và chu vi bằng 40cm. Để giải bài toán này, ta cần:
- Gọi đường chéo nhỏ là x, thì đường chéo lớn là 2x
- Áp dụng định lý Pytago để tìm cạnh hình thoi
- Lập phương trình với chu vi đã cho
Giải phương trình sẽ cho ta đường chéo nhỏ là 6cm và đường chéo lớn là 12cm. Từ đó xác nhận lại độ dài cạnh hình thoi là 10cm, phù hợp với chu vi 40cm đã cho.
Ứng dụng thực tế của chu vi hình thoi trong toán học và đời sống
Chu vi hình thoi được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của cuộc sống. Việc tính toán và áp dụng các tính chất của hình thoi giúp giải quyết nhiều bài toán thực tiễn một cách hiệu quả.
Trong thực tế, các kiến trúc sư và kỹ sư thường xuyên sử dụng tính chất của hình thoi để thiết kế các công trình. Theo Trang web về toán, việc nắm vững cách tính chu vi và diện tích hình thoi sẽ giúp tối ưu hóa việc sử dụng vật liệu và không gian.
Ứng dụng hình thoi trong toán học còn thể hiện qua việc giải các bài toán phức tạp về hình học không gian, đặc biệt trong các bài toán liên quan đến lập phương và hình chóp đều.
Giải quyết các bài toán thực tế
Trong ngành công nghiệp dệt may, việc tính toán chu vi hình thoi giúp xác định chính xác lượng vải cần thiết cho các mẫu thiết kế có hình dạng thoi. Các nhà thiết kế thời trang thường sử dụng mẫu hình thoi để tạo ra những họa tiết độc đáo trên trang phục.
Ngành nông nghiệp cũng áp dụng kiến thức về hình thoi trong việc thiết kế hệ thống tưới tiêu. Các kỹ sư nông nghiệp tính toán chu vi các mảnh đất hình thoi để lắp đặt hệ thống ống dẫn nước hiệu quả nhất.
Ứng dụng trong thiết kế và xây dựng
Trong kiến trúc hiện đại, hình thoi được sử dụng phổ biến cho các mái vòm và cửa sổ. Ví dụ điển hình là Nhà hát Opera Sydney, nơi các tấm kính hình thoi được ghép lại tạo thành những mái vòm đặc trưng.
Các kỹ sư xây dựng thường sử dụng cấu trúc hình thoi trong thiết kế cầu treo. Việc tính toán chính xác chu vi các thanh giằng hình thoi giúp đảm bảo độ bền và tính thẩm mỹ của công trình.
Trong lĩnh vực thiết kế nội thất, các nhà thiết kế thường sử dụng gạch lát sàn hình thoi để tạo điểm nhấn và mang lại cảm giác không gian rộng rãi hơn cho căn phòng.
Khi nghiên cứu về chu vi hình thoi, chúng ta nhận thấy rằng việc hiểu rõ định nghĩa, đặc điểm và công thức tính của hình thoi là rất quan trọng. Chu vi hình thoi được tính dễ dàng nhờ vào công thức đơn giản P = 4a. Việc nắm vững kiến thức này không chỉ hữu ích trong học tập mà còn giúp giải quyết các bài toán thực tế trong cuộc sống hàng ngày. Hãy vận dụng kiến thức về chu vi hình thoi để nâng cao kỹ năng toán học của bạn!




