Chu vi kí hiệu là gì? Đây là câu hỏi thường gặp trong học tập và nghiên cứu hình học. Ký hiệu chu vi giúp nắm bắt nhanh thông tin trong các công thức toán học. Tìm hiểu rõ về nội dung này sẽ giúp bạn có kiến thức vững chắc khi làm việc với các hình học khác nhau và giải quyết bài toán một cách hiệu quả.
Chu vi kí hiệu là gì?
Chu vi thường được kí hiệu chu vi là chữ P (Perimeter) hoặc C (Circumference) trong toán học. Đây là những ký hiệu của chu vi phổ biến được sử dụng rộng rãi trong các tài liệu giáo khoa và sách tham khảo. Việc thống nhất cách viết giúp học sinh dễ dàng tiếp cận và ghi nhớ.
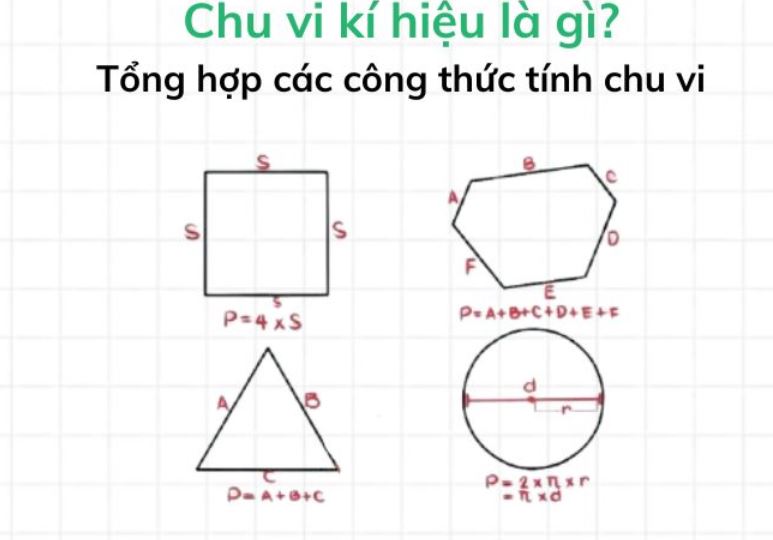
Trong các bài toán thực tế, chu vi kí hiệu là gì thường được giải thích rõ ràng ngay từ đầu để tránh nhầm lẫn. Ví dụ khi giải bài toán về hình tròn, chu vi thường được kí hiệu là C. Còn với các hình đa giác như tam giác, tứ giác, chu vi thường được kí hiệu là P. Theo Học Thế Nào, việc phân biệt và sử dụng đúng kí hiệu sẽ giúp học sinh nắm vững kiến thức cơ bản.
Ngoài ra, trong một số tài liệu chuyên ngành, chu vi còn có thể được kí hiệu bằng các chữ cái khác tùy theo quy ước của từng lĩnh vực. Tuy nhiên, P và C vẫn là hai kí hiệu phổ biến và được sử dụng rộng rãi nhất trong toán học phổ thông.
Các khái niệm cơ bản về chu vi trong hình học phẳng
Trong Hình học phẳng, chu vi là một trong những khái niệm quan trọng nhất. Việc nắm vững các khái niệm cơ bản về chu vi giúp giải quyết nhiều bài toán thực tiễn và phát triển tư duy không gian.
Định nghĩa và ý nghĩa của chu vi trong toán học
Chu vi là gì? Đó là độ dài đường biên bao quanh một hình phẳng, được tính bằng tổng độ dài các cạnh của hình. Khái niệm này xuất hiện từ thời Ai Cập cổ đại, khi con người cần đo đạc chu vi các thửa ruộng để tính thuế.
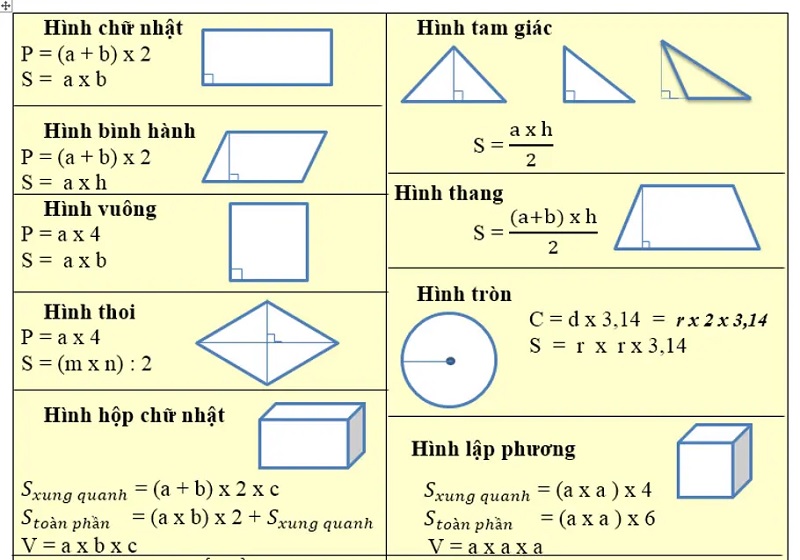
Trong thực tế, chu vi có ý nghĩa quan trọng trong nhiều lĩnh vực như xây dựng, kiến trúc và thiết kế. Ví dụ, khi thiết kế hàng rào cho một khu đất, kiến trúc sư cần tính toán chính xác chu vi để ước tính số lượng vật liệu cần thiết.
Phân biệt chu vi và diện tích trong hình học
Diện tích và chu vi là hai đại lượng độc lập trong hình học. Diện tích đo lường phần không gian bên trong hình, trong khi chu vi đo độ dài đường viền bao quanh hình.
Một minh họa thực tế từ công trình nghiên cứu của GS. John Conway (Đại học Princeton) cho thấy: Hai hình có cùng chu vi có thể có diện tích khác nhau và ngược lại. Điều này được ứng dụng rộng rãi trong thiết kế kiến trúc tối ưu.
Sự khác biệt này đặc biệt quan trọng trong quy hoạch đô thị và thiết kế cảnh quan, nơi cần cân nhắc cả hai yếu tố để tạo ra không gian hợp lý và hiệu quả.
Đơn vị đo chu vi thường dùng
Đơn vị đo chu vi thuộc hệ đo chiều dài, phổ biến nhất là mét (m) và các đơn vị liên quan. Trong công nghiệp và xây dựng, milimét (mm) thường được sử dụng cho độ chính xác cao.
Tại Mỹ và một số quốc gia khác, đơn vị inch và foot vẫn được dùng phổ biến. Theo khảo sát của Hiệp hội Đo lường Quốc tế (2022), 90% các nước trên thế giới sử dụng hệ mét làm đơn vị đo chu vi chính thức.
Việc chuyển đổi giữa các đơn vị đo chu vi cần tuân theo quy tắc nhất định để đảm bảo tính chính xác trong tính toán và ứng dụng thực tế.
Cách biểu diễn và sử dụng kí hiệu chu vi trong các công thức toán học
Kí hiệu chu vi là P hay C được sử dụng phổ biến trong các công thức toán học. Việc lựa chọn kí hiệu phụ thuộc vào quy ước và thói quen sử dụng của từng quốc gia, trường phái toán học.
Trong toán học phổ thông, các kí hiệu này giúp đơn giản hóa cách viết công thức và biểu thức. Thay vì phải viết dài dòng “chu vi hình…”, việc sử dụng kí hiệu giúp trình bày ngắn gọn, dễ hiểu và chuyên nghiệp hơn.
Các kí hiệu chu vi phổ biến (P và C)
Chu vi kí hiệu là gì phụ thuộc vào từng hệ thống giáo dục. Tại Việt Nam, kí hiệu P (Perimeter) được sử dụng phổ biến hơn trong sách giáo khoa và giảng dạy. Kí hiệu C (Circumference) thường được dùng trong các tài liệu nước ngoài, đặc biệt là các nước nói tiếng Anh.
Mỗi kí hiệu đều có ưu điểm riêng. P dễ phân biệt với diện tích (S), trong khi C dễ nhớ vì liên quan đến từ gốc tiếng Anh. Tuy nhiên, cả hai đều được chấp nhận và sử dụng rộng rãi trong cộng đồng toán học.
Quy tắc sử dụng kí hiệu chu vi trong bài toán
Khi sử dụng kí hiệu chu vi trong bài toán, cần tuân thủ một số nguyên tắc cơ bản. Kí hiệu phải được định nghĩa rõ ràng ngay từ đầu bài giải. Nếu sử dụng nhiều hình trong một bài toán, cần thêm chỉ số phân biệt (P1, P2…).
Việc sử dụng kí hiệu phải nhất quán xuyên suốt bài giải. Không được thay đổi giữa P và C trong cùng một bài toán để tránh gây nhầm lẫn cho người đọc.
Cách viết công thức với kí hiệu chu vi
Công thức chu vi cần được trình bày rõ ràng, có thứ tự logic. Kí hiệu chu vi luôn được đặt ở vế trái của phương trình. Các thành phần trong công thức phải được phân tách bằng dấu phép tính phù hợp.
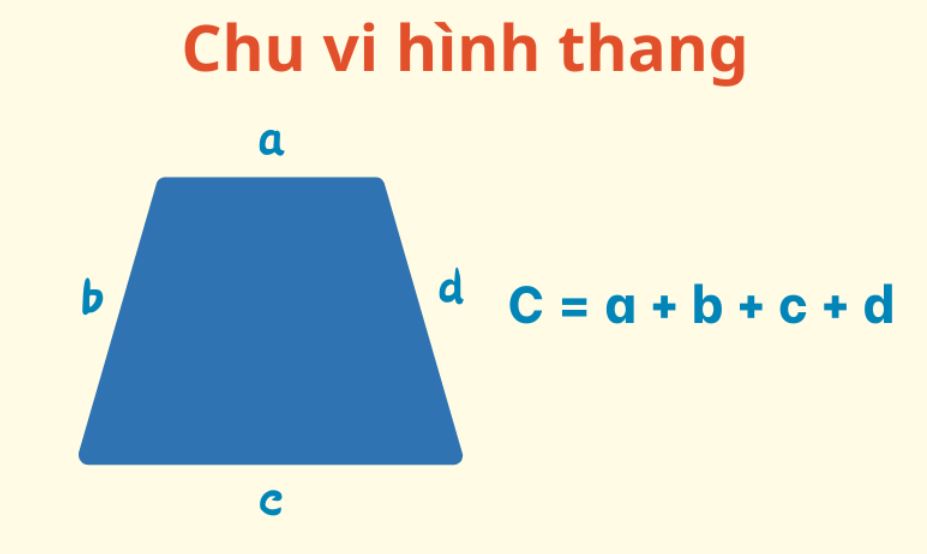
Khi viết công thức phức tạp, nên chia thành nhiều bước nhỏ để dễ theo dõi. Mỗi bước tính toán cần có giải thích ngắn gọn về cách áp dụng công thức.
Cách trình bày lời giải sử dụng kí hiệu chu vi
Lời giải cần được trình bày theo trình tự: Cho dữ kiện – Áp dụng công thức – Tính toán kết quả. Mỗi bước tính phải được viết trên một dòng riêng, có đánh số thứ tự rõ ràng.
Kết quả cuối cùng cần được khoanh tròn hoặc gạch chân để nổi bật. Đơn vị đo lường phải được ghi kèm theo kết quả một cách chính xác và nhất quán.
Công thức tính chu vi các hình cơ bản
Chu vi kí hiệu là C hoặc P (Perimeter), dùng để chỉ độ dài đường biên bao quanh một hình phẳng. Việc tính chu vi các hình cơ bản là kiến thức nền tảng quan trọng trong hình học, giúp giải quyết nhiều bài toán thực tế.
Công thức tính chu vi hình vuông
Chu vi hình vuông được tính bằng tổng độ dài 4 cạnh bằng nhau. Với a là độ dài cạnh, công thức là C = 4a. Ví dụ một hình vuông có cạnh 5cm sẽ có chu vi là 20cm.
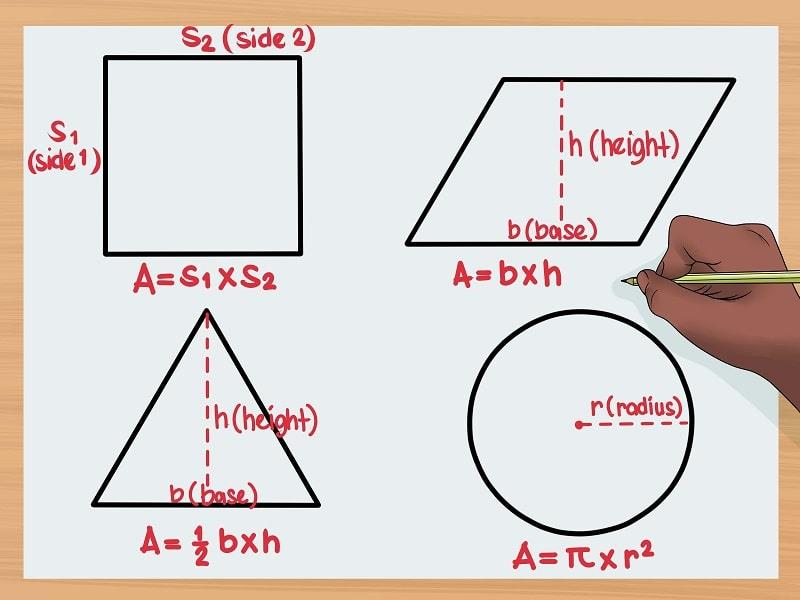
Tính chất đặc biệt của hình vuông là 4 cạnh bằng nhau và 4 góc vuông, giúp việc tính toán chu vi trở nên đơn giản. Trong thực tế, công thức này thường được áp dụng để tính chu vi các vật thể vuông vức như khung tranh, mặt bàn vuông.
Công thức tính chu vi hình chữ nhật
Chu vi hình chữ nhật được tính theo công thức C = 2(a + b), trong đó a là chiều dài và b là chiều rộng. Công thức này dựa trên nguyên lý cộng độ dài của 2 cặp cạnh song song.
Khi áp dụng, cần chú ý phân biệt rõ chiều dài và chiều rộng. Đây là công thức phổ biến trong kiến trúc và thiết kế, giúp tính toán lượng vật liệu cần thiết cho các công trình có dạng hình chữ nhật.
Công thức tính chu vi hình tròn
Chu vi hình tròn được tính theo công thức C = 2πR hoặc C = πD, với R là bán kính và D là đường kính. π là hằng số có giá trị xấp xỉ 3,14 hoặc 22/7.
Công thức này phản ánh mối quan hệ giữa chu vi và bán kính hình tròn, là cơ sở cho nhiều ứng dụng trong kỹ thuật và công nghiệp. Ví dụ, khi thiết kế bánh xe, đĩa tròn hay các chi tiết máy có dạng tròn.
Công thức tính chu vi đa giác đều
Chu vi đa giác đều bằng tích của số cạnh và độ dài một cạnh: C = n.a, với n là số cạnh và a là độ dài mỗi cạnh. Đa giác đều có đặc điểm các cạnh bằng nhau và các góc bằng nhau.
Công thức này áp dụng cho mọi đa giác đều từ tam giác đều, lục giác đều đến các đa giác có nhiều cạnh hơn. Trong thực tế, các công trình kiến trúc và thiết kế thường sử dụng hình dạng đa giác đều vì tính đối xứng và thẩm mỹ.
Hướng dẫn giải bài tập về chu vi với các ví dụ minh họa
Chu vi kí hiệu là P hoặc C, được dùng để chỉ độ dài đường biên của một hình. Cách tính chu vi phụ thuộc vào loại hình học, thường bằng tổng độ dài các cạnh với hình đa giác hoặc công thức riêng với hình tròn.
Để giải các bài toán về chu vi hiệu quả, cần nắm vững công thức và phương pháp tính toán phù hợp với từng dạng hình. Dưới đây là hướng dẫn chi tiết giúp giải quyết các bài tập về chu vi một cách dễ dàng.
Phương pháp giải bài toán chu vi cơ bản
Bước đầu tiên là xác định loại hình cần tính chu vi. Với hình chữ nhật, chu vi bằng tổng độ dài 4 cạnh. Với hình vuông, chu vi bằng 4 lần độ dài cạnh.
Tiếp theo, kiểm tra kỹ các dữ kiện đã cho trong đề bài. Cần chú ý đơn vị đo và quy đổi về cùng đơn vị nếu cần thiết.
Cuối cùng, áp dụng công thức tính chu vi phù hợp và thực hiện tính toán. Ví dụ về chu vi hình chữ nhật có chiều dài 5cm, chiều rộng 3cm: P = 2(a + b) = 2(5 + 3) = 16cm.
Bài tập mẫu về tính chu vi các hình
Một khu vườn hình vuông có cạnh 10m cần rào chắn xung quanh. Để tính chi phí làm hàng rào, ta tính chu vi: P = 4a = 4 × 10 = 40m.
Với hình tròn bán kính 5cm, chu vi được tính theo công thức: C = 2πR = 2 × 3,14 × 5 = 31,4cm.
Đối với hình tam giác, chu vi là tổng độ dài ba cạnh. Tam giác có các cạnh 3cm, 4cm và 5cm có chu vi: P = 3 + 4 + 5 = 12cm.
Các dạng bài tập thường gặp
Bài toán tìm chu vi khi biết cạnh
Dạng bài này yêu cầu áp dụng trực tiếp công thức tính chu vi. Với hình vuông cạnh 6cm, chu vi là 24cm.
Với hình chữ nhật có chiều dài 8cm và chiều rộng 5cm, chu vi là 26cm. Việc tính toán đơn giản giúp học sinh làm quen với khái niệm chu vi.
Bài toán tìm cạnh khi biết chu vi
Dạng bài này đòi hỏi kỹ năng biến đổi công thức. Ví dụ: Hình vuông có chu vi 20cm, cần tìm độ dài cạnh.
Ta có: P = 4a → a = P/4 = 20/4 = 5cm. Với hình chữ nhật, nếu biết chu vi và một cạnh, có thể tìm được cạnh còn lại thông qua biến đổi công thức.
Chu vi kí hiệu là gì? Đây là câu hỏi phổ biến khi học về hình học phẳng. Trong bài viết này, bạn đã tìm hiểu về định nghĩa, cách tính cũng như các công thức liên quan đến chu vi của nhiều hình như hình vuông, hình chữ nhật, và hình tròn. Việc nắm vững kiến thức này không chỉ giúp bạn giải toán hiệu quả mà còn tạo nền tảng vững chắc cho những kiến thức toán học cao hơn. Hãy áp dụng những gì đã học vào thực tế để củng cố kỹ năng của mình!




