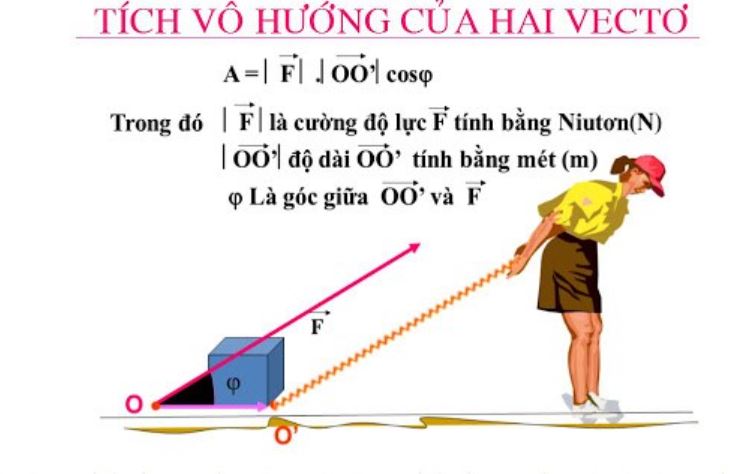
Tích vô hướng của hai vectơ: Công thức, tính chất và ứng dụng trong toán học

Tích vô hướng của hai vectơ là phép toán cơ bản trong hình học vector, đóng vai trò quan trọng trong nhiều lĩnh vực. Bài viết sẽ trình bày công thức cũng như phương pháp tính tích vô hướng, giúp bạn hiểu rõ cách áp dụng trong các bài toán thực tiễn. Khám phá tính chất và ứng dụng của phép toán này qua các ví dụ minh họa cụ thể.

Tích vô hướng của hai vectơ là phép toán cơ bản trong hình học vector

Tích vô hướng là gì – phép toán số học giữa hai vector, cho kết quả là một số vô hướng. Phép toán này có vai trò quan trọng trong việc tính góc giữa hai vector và xác định tính vuông góc của chúng. Kết quả của phép nhân này phụ thuộc vào độ dài của hai vector và góc giữa chúng.

Trong không gian toán học, tích vô hướng của hai vectơ được tính bằng tích độ dài hai vector nhân với cosin góc tạo bởi chúng. Công thức tổng quát là: a.b = |a|.|b|.cos(α), trong đó |a| và |b| là độ dài của hai vector, α là góc giữa chúng. Ví dụ, khi hai vector vuông góc (α = 90°), tích vô hướng bằng 0 vì cos(90°) = 0.

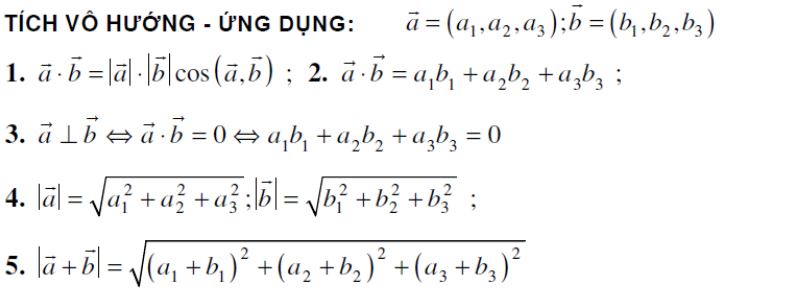
Ứng dụng của tích vô hướng rất đa dạng trong thực tế. Trong vật lý, tích vô hướng giúp tính công của lực khi vật chuyển động. Theo nghiên cứu của Viện Khoa học và Công nghệ Việt Nam, phép toán này còn được sử dụng rộng rãi trong xử lý ảnh số, nhận dạng mẫu và học máy. Đặc biệt trong trí tuệ nhân tạo, tích vô hướng là công cụ quan trọng để tính toán độ tương đồng giữa các vector đặc trưng.

Công thức tính tích vô hướng của hai vectơ trong mặt phẳng và không gian

Tích vô hướng là phép toán quan trọng trong hình học vectơ, giúp xác định mối quan hệ giữa các vectơ. Công thức tích vô hướng được áp dụng rộng rãi trong hình học phẳng Oxy và không gian ba chiều.

Công thức tính tích vô hướng qua tọa độ trong mặt phẳng Oxy

Trong mặt phẳng tọa độ Oxy, với hai vectơ a(x₁,y₁) và b(x₂,y₂), tích vô hướng được tính bằng tổng tích các tọa độ tương ứng: a.b = x₁x₂ + y₁y₂. Công thức này giúp tính toán nhanh chóng mà không cần xác định góc giữa hai vectơ.

Ví dụ khi tính tích vô hướng của vectơ a(2,3) và b(-1,4), ta có: a.b = 2.(-1) + 3.4 = -2 + 12 = 10.

Công thức tính tích vô hướng trong không gian Oxyz

Tích vô hướng của hai vectơ trong không gian Oxyz được mở rộng với thêm tọa độ z. Với hai vectơ a(x₁,y₁,z₁) và b(x₂,y₂,z₂), công thức tính là: a.b = x₁x₂ + y₁y₂ + z₁z₂.

Phép tính này có tính chất giao hoán và phân phối đối với phép cộng vectơ. Kết quả luôn là một số thực, không phải là một vectơ.

Công thức tính tích vô hướng qua độ dài và góc giữa hai vectơ

Công thức tính tích vô hướng qua độ dài và góc α giữa hai vectơ được biểu diễn: a.b = |a|.|b|.cosα. Công thức này đặc biệt hữu ích khi cần xác định góc giữa hai vectơ.

Khi α = 90°, cosα = 0 nên tích vô hướng bằng 0, cho thấy hai vectơ vuông góc. Khi α = 0°, cosα = 1, tích vô hướng đạt giá trị lớn nhất, chứng tỏ hai vectơ cùng phương cùng chiều.

Các tính chất quan trọng của tích vô hướng hai vectơ

Tích vô hướng của hai vectơ là một phép toán cơ bản và quan trọng trong hình học vector. Phép toán này cho phép ta tính toán góc giữa hai vector, xác định tính vuông góc và đo độ dài của vector.

Để hiểu rõ hơn về các tính chất của tích vô hướng, ta cần xem xét từng đặc điểm cụ thể thông qua các tính chất cơ bản. Mỗi tính chất sẽ giúp giải quyết các bài toán vector khác nhau một cách hiệu quả.

Tính chất giao hoán và phân phối

Tích vô hướng tuân theo hai tính chất quan trọng. Tính chất giao hoán cho phép hoán đổi vị trí hai vector mà không làm thay đổi kết quả: a.b = b.a. Điều này giúp đơn giản hóa các phép tính phức tạp.

Tính chất phân phối thể hiện qua công thức: a.(b + c) = a.b + a.c. Tính chất này rất hữu ích khi phân tích các vector thành tổng của các vector thành phần, đặc biệt trong các bài toán về lực và chuyển động.

Điều kiện để hai vectơ vuông góc với nhau

Hai vecto vuông góc khi và chỉ khi tích vô hướng của chúng bằng 0. Đây là một trong những ứng dụng quan trọng nhất của tích vô hướng trong hình học không gian.

Khi hai vecto vuông góc khi nào? Câu trả lời nằm ở góc giữa chúng phải bằng 90 độ. Trong trường hợp này, cos của góc giữa hai vector bằng 0, dẫn đến tích vô hướng cũng bằng 0.

Ngược lại, nếu hai vector không vuông góc, chúng có thể 2 vecto cùng phương hoặc tạo thành một góc bất kỳ khác 90 độ.

Mối liên hệ giữa tích vô hướng và độ dài vectơ

Tích vô hướng của một vector với chính nó cho ta bình phương độ dài của vector đó. Công thức này được viết dưới dạng: a.a = |a|².

Mối liên hệ này có ý nghĩa đặc biệt trong việc tính toán độ dài vector. Thay vì phải tính căn bậc hai của tổng bình phương các thành phần, ta có thể sử dụng tích vô hướng để đơn giản hóa quá trình tính toán.

Ngoài ra, tích vô hướng còn cho phép ta tính góc giữa hai vector thông qua công thức: cos α = (a.b)/(|a|.|b|). Đây là công cụ quan trọng trong nhiều ứng dụng thực tế như tính toán công của lực hay xác định hướng chuyển động.

Phương pháp giải các bài toán về tích vô hướng

Tích vô hướng là một phép toán quan trọng trong hình học vector, giúp giải quyết nhiều bài toán về góc và khoảng cách. Để giải các bài toán liên quan đến cách tính tích vô hướng, cần nắm vững công thức cơ bản và các tính chất.

Việc áp dụng tích vô hướng đòi hỏi sự linh hoạt trong việc chọn phương pháp phù hợp. Có thể sử dụng công thức trực tiếp hoặc thông qua các vector trung gian để đơn giản hóa phép tính.

Các dạng bài tập thường gặp

Dạng bài tập về tích vô hướng 2 vecto thường xuất hiện dưới nhiều hình thức khác nhau. Phổ biến nhất là các bài toán yêu cầu tính góc giữa hai vector, chứng minh hai vector vuông góc hoặc tìm độ dài vector.

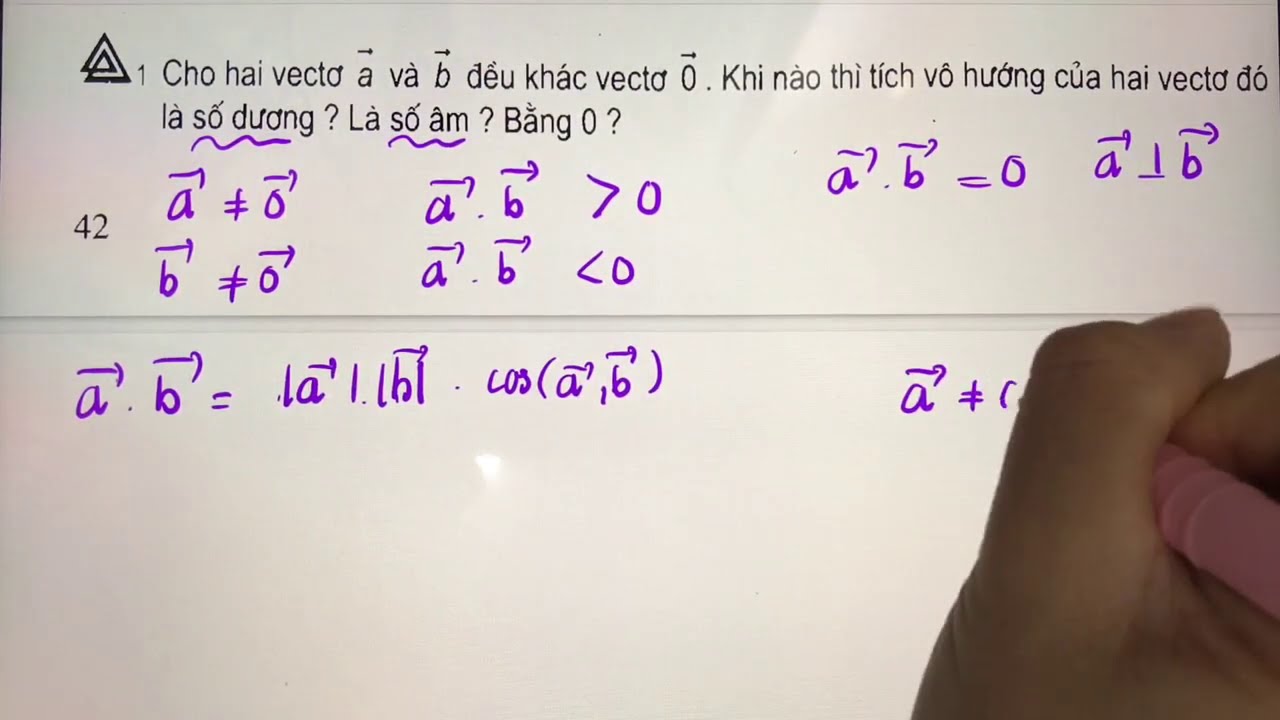
Một dạng bài tập nâng cao là sử dụng tích vô hướng để chứng minh các bất đẳng thức hình học. Trong trường hợp này, việc biến đổi biểu thức tích vô hướng thành tích có hướng của 2 vecto có thể giúp đơn giản hóa bài toán.

Phương pháp tính góc giữa hai vectơ

Khi tính góc giữa hai vector, công thức cơ bản là cosα = (a.b)/(|a|.|b|). Việc áp dụng công thức cần chú ý đến dấu của tích vô hướng và độ lớn của các vector.

Trong nhiều trường hợp, có thể sử dụng tính chất của tích vô hướng để đơn giản hóa phép tính. Ví dụ, nếu hai vector có độ dài bằng 1, góc giữa chúng chỉ phụ thuộc vào tích vô hướng của chúng.

Cách chứng minh hai vectơ vuông góc

Để chứng minh hai vector vuông góc, cần chứng minh tích vô hướng của chúng bằng 0. Phương pháp này dựa trên định nghĩa hình học của tích vô hướng.

Trong một số trường hợp phức tạp, có thể sử dụng phép biến đổi tương đương hoặc đưa về hệ tọa độ để đơn giản hóa việc chứng minh. Việc chọn hệ tọa độ phù hợp đóng vai trò quan trọng trong việc giải quyết bài toán.

Ngoài ra, có thể sử dụng các tính chất đặc biệt như: nếu hai vector vuông góc với cùng một vector thứ ba, thì chúng song song với nhau. Điều này mở rộng khả năng giải quyết các bài toán phức tạp hơn.

Ứng dụng của tích vô hướng trong hình học và vật lý

Tích vô hướng là một công cụ toán học quan trọng được ứng dụng rộng rãi trong nhiều lĩnh vực, đặc biệt là hình học và vật lý. Tích vô hướng của hai vectơ giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả và trực quan. Việc áp dụng công thức tích vô hướng của hai vectơ còn hỗ trợ đắc lực trong việc tính toán các đại lượng vật lý như công, năng lượng.

Trong các ứng dụng thực tế, tích vô hướng thường được kết hợp với các công cụ toán học khác như khai triển nhị thức newton để giải quyết các bài toán phức tạp. Đồng thời, việc áp dụng bđt bunhiacopxki cũng giúp tối ưu hóa các phép tính liên quan đến tích vô hướng.

Tính công của lực trong vật lý

Trong vật lý, tích vô hướng đóng vai trò then chốt khi tính công của một lực. Công được định nghĩa là tích vô hướng của vectơ lực và vectơ dịch chuyển, phản ánh năng lượng được truyền từ lực tác dụng lên vật.

Khi lực không đổi và chuyển động thẳng, công thức tính công trở nên đơn giản. Tuy nhiên, trong thực tế, nhiều trường hợp lực thay đổi theo thời gian hoặc theo vị trí, đòi hỏi phải áp dụng tích phân để tính toán chính xác giá trị công.

Ví dụ thực tế từ nghiên cứu của GS. David J. Griffiths (Đại học Reed) cho thấy việc tính công của lực điện trường yêu cầu hiểu biết sâu sắc về tích vô hướng và ứng dụng của nó trong các phép tính tích phân đường.

Giải các bài toán hình học không gian

Tích vô hướng là công cụ đắc lực trong việc giải quyết các bài toán hình học không gian. Nó giúp xác định góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, cũng như khoảng cách từ điểm đến mặt phẳng một cách hiệu quả.

Trong các bài toán về đa diện, tích vô hướng được sử dụng để tính diện tích, thể tích và các yếu tố metric khác. Việc kết hợp với các phép biến đổi tọa độ giúp đơn giản hóa quá trình giải quyết nhiều bài toán phức tạp.

Các ứng dụng trong thiết kế đồ họa 3D và mô phỏng không gian cũng dựa nhiều vào tích vô hướng. Theo nghiên cứu của Viện Công nghệ Massachusetts (MIT), các phần mềm thiết kế CAD hiện đại sử dụng tích vô hướng như một công cụ cơ bản trong các thuật toán xử lý hình học.

Tích vô hướng của hai vectơ là phép toán cơ bản trong hình học vector, cho phép chúng ta hiểu sâu hơn về mối quan hệ giữa các vectơ trong không gian. Các công thức và tính chất của phép toán này không chỉ hữu ích trong tính toán mà còn trong việc giải quyết nhiều bài toán thực tiễn. Bằng cách nắm vững kiến thức về tích vô hướng của hai vectơ, bạn sẽ phát triển kỹ năng giải toán một cách hiệu quả và tự tin hơn.