Cách chứng minh hình lục giác đều qua tính chất và ứng dụng trong hình học

Chứng minh hình lục giác đều là một chủ đề thú vị trong hình học, giúp người học phát triển tư duy logic. Qua các phương pháp đơn giản, hành trình khám phá tính chất và ứng dụng của hình lục giác đều sẽ trở nên dễ dàng hơn. Hãy cùng tìm hiểu cách chứng minh những khía cạnh quan trọng của hình lục giác đều trong bài viết này.

Chứng minh hình lục giác đều và các phương pháp cơ bản

Để chứng minh hình lục giác đều, cần dựa vào các tính chất đặc trưng của loại hình này. Trước khi đi vào các phương pháp chứng minh, bạn có thể tham khảo thêm về hình lục giác đều là gì để nắm rõ các khái niệm cơ bản.

Phương pháp chứng minh đầu tiên là dựa vào định nghĩa. Một hình lục giác được gọi là đều khi có 6 cạnh bằng nhau và 6 góc bằng nhau. Do đó, để chứng minh ta cần chỉ ra 6 cạnh có độ dài bằng nhau và 6 góc đều bằng 120°. Đây là phương pháp trực tiếp và dễ áp dụng nhất.

Phương pháp thứ hai là sử dụng tính chất đối xứng. Một hình lục giác đều có 6 trục đối xứng đi qua các đỉnh đối diện và 6 trục đối xứng đi qua trung điểm các cạnh đối diện. Nếu chứng minh được hình có các trục đối xứng này, ta có thể kết luận đó là hình lục giác đều.

Ngoài ra, có thể sử dụng phương pháp chứng minh gián tiếp thông qua các tam giác đều. Một hình lục giác đều có thể được chia thành 6 tam giác đều bằng nhau có chung tâm. Nếu chứng minh được 6 tam giác này đều và bằng nhau, ta có thể kết luận hình ban đầu là hình lục giác đều. Để tìm hiểu thêm nhiều kiến thức toán học hữu ích khác, bạn có thể truy cập Website toán học.

Phương pháp cuối cùng là sử dụng các cách chứng minh hình lục giác đều thông qua đường tròn ngoại tiếp và nội tiếp. Nếu một hình lục giác có thể nội tiếp và ngoại tiếp được trong hai đường tròn đồng tâm, đồng thời các đỉnh của nó cách đều tâm đường tròn, thì đó chính là hình lục giác đều.

Các tính chất quan trọng để chứng minh hình lục giác đều

Hình lục giác đều là một đa giác đặc biệt với nhiều tính chất độc đáo. Việc chứng minh một hình lục giác là hình lục giác đều đòi hỏi phải xét đến ba yếu tố cốt lõi: độ dài các cạnh, số đo các góc và các đường chéo.

Để chứng minh một hình lục giác là hình lục giác đều, cần phải chứng minh được các tính chất về cạnh, góc và đường chéo. Mỗi tính chất đều có vai trò quan trọng và bổ trợ cho nhau trong quá trình chứng minh.

Chứng minh sáu cạnh bằng nhau trong hình lục giác đều

Chứng minh hình lục giác đều có sáu cạnh bằng nhau là bước đầu tiên và quan trọng nhất. Để chứng minh điều này, ta có thể sử dụng phương pháp tam giác đồng dạng hoặc phương pháp đường tròn ngoại tiếp.

Khi vẽ các đường chéo nối các đỉnh đối diện, hình lục giác đều được chia thành 6 tam giác đều bằng nhau. Các tam giác này có chung tâm là tâm của hình lục giác đều và có cạnh chính là các cạnh của hình lục giác.

Từ tính chất của tam giác đều, ta suy ra các cạnh của hình lục giác phải bằng nhau và bằng bán kính đường tròn ngoại tiếp hình lục giác đều.

Chứng minh các góc bằng nhau trong hình lục giác đều

Chứng minh hình lục giác đều có góc bằng nhau là bước tiếp theo trong quá trình chứng minh. Mỗi góc trong của hình lục giác đều có số đo 120 độ.

Tổng số đo các góc trong của hình lục giác là (6-2) × 180° = 720°. Do tính đối xứng của hình lục giác đều, các góc phải bằng nhau và mỗi góc có số đo là 720° ÷ 6 = 120°.

Có thể kiểm chứng bằng cách vẽ các đường phân giác góc, các đường này sẽ đồng quy tại tâm của hình lục giác và chia hình thành 6 phần bằng nhau.

Chứng minh đường chéo trong hình lục giác đều

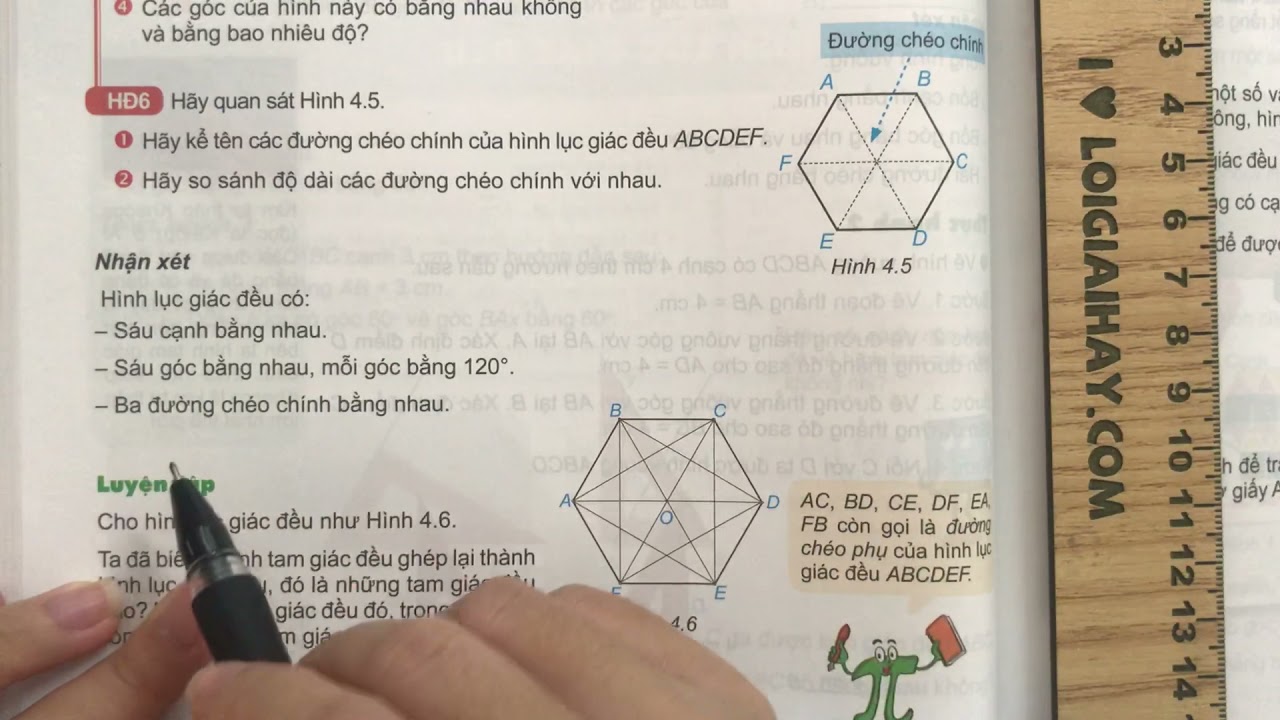
Đường chéo hình lục giác đều có những tính chất đặc biệt cần được chứng minh. Trong hình lục giác đều, các đường chéo nối hai đỉnh đối diện đều bằng nhau và đi qua tâm.

Các đường chéo của hình lục giác đều chia nhau thành các phần bằng nhau tại tâm. Điều này có thể chứng minh thông qua tính chất đối xứng và sự đồng dạng của các tam giác được tạo thành.

Khoảng cách từ tâm đến mỗi đỉnh của hình lục giác đều bằng nhau và bằng bán kính của đường tròn ngoại tiếp. Đây là cơ sở để chứng minh các đường chéo bằng nhau và cắt nhau tại tâm của hình.

Phương pháp chứng minh tính đối xứng của hình lục giác đều

Để chứng minh tính đối xứng của hình lục giác đều, ta cần xét hai yếu tố quan trọng là tâm đối xứng và các trục đối xứng. Việc chứng minh này dựa trên các tính chất hình học cơ bản về đường thẳng, góc và khoảng cách. Như bạn có thể tham khảo thêm hình lục giác đều có mấy trục đối xứng, ta sẽ phân tích chi tiết từng yếu tố.

Chứng minh tâm đối xứng

Để chứng minh tâm đối xứng của hình lục giác đều, ta bắt đầu bằng việc xác định tâm O của hình. Tâm O chính là giao điểm của ba đường chéo nối các đỉnh đối diện của hình lục giác.

Khi lấy một điểm bất kỳ A trên hình lục giác và vẽ đoạn thẳng từ tâm O đến điểm A, sau đó kéo dài đoạn thẳng này một đoạn bằng OA, ta sẽ được điểm A’ nằm trên hình lục giác. Điều này luôn đúng với mọi điểm trên hình lục giác.

Tính chất này được chứng minh thông qua việc các cạnh của hình lục giác đều bằng nhau và các góc đều bằng 120°. Do đó, khi quay hình 180° quanh tâm O, hình lục giác sẽ trùng khớp với chính nó.

Chứng minh các trục đối xứng

Để chứng minh hình lục giác đều có sáu trục đối xứng, ta xét hai loại trục: trục nối hai đỉnh đối diện và trục đi qua trung điểm hai cạnh đối diện.

Với trục nối hai đỉnh đối diện, ta có ba trục. Mỗi trục này chia hình lục giác thành hai phần bằng nhau và vuông góc với đoạn thẳng nối hai đỉnh còn lại. Các góc tạo bởi hai trục liên tiếp luôn bằng 60°.

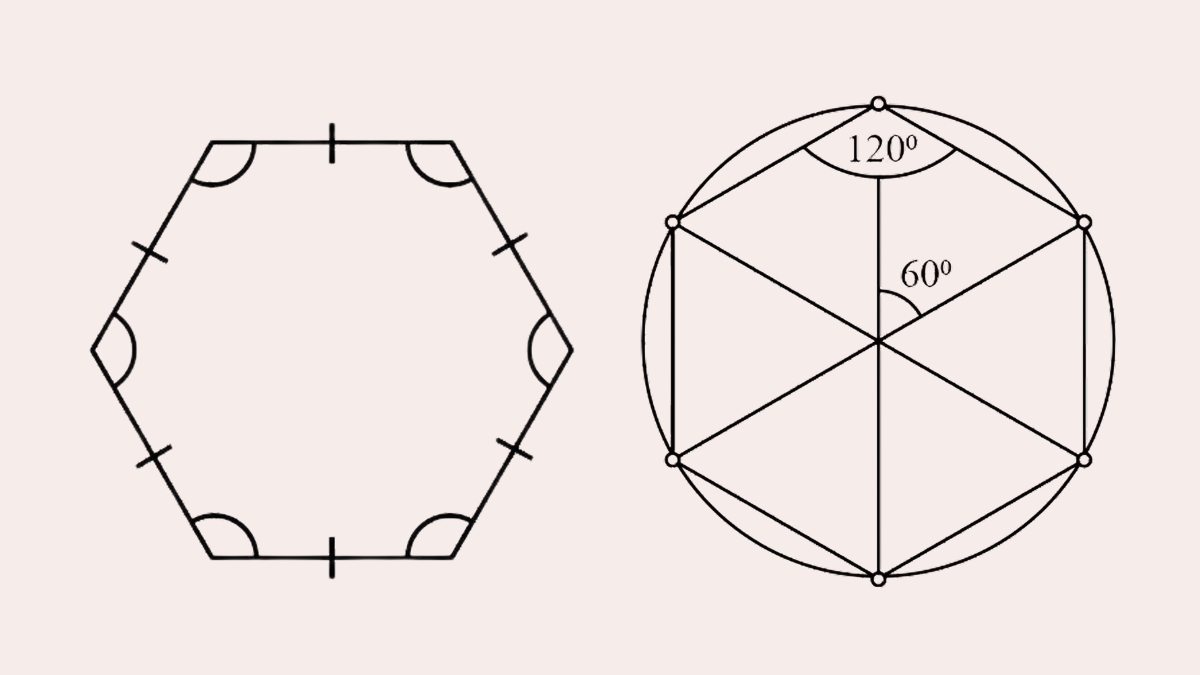
Ba trục còn lại đi qua trung điểm các cạnh đối diện. Các trục này cũng chia hình lục giác thành hai phần bằng nhau và vuông góc với cạnh tương ứng. Khi gập hình theo bất kỳ trục nào trong sáu trục này, hai nửa hình sẽ trùng khớp hoàn toàn.

Chứng minh hình lục giác đều nội tiếp đường tròn

Để chứng minh hình lục giác đều nội tiếp đường tròn, ta cần xác định các tính chất đặc trưng của hình lục giác đều và mối quan hệ của nó với đường tròn ngoại tiếp. Một hình lục giác đều có 6 cạnh bằng nhau và 6 góc bằng nhau, mỗi góc có số đo 120°.

Khi một hình lục giác đều được nội tiếp trong đường tròn, tất cả các đỉnh của nó đều nằm trên đường tròn và cách đều tâm đường tròn. Điều này tạo nên một cấu trúc hình học hoàn hảo và đối xứng.

Các bước chứng minh

Bước 1: Xét hình lục giác ABCDEF nội tiếp đường tròn tâm O. Nối O với tất cả các đỉnh của lục giác.

Bước 2: Do các đỉnh của lục giác đều nằm trên đường tròn, các đoạn OA, OB, OC, OD, OE, OF là các bán kính của đường tròn nên bằng nhau.

Bước 3: Xét hai tam giác kề nhau bất kỳ được tạo bởi hai bán kính liên tiếp, ví dụ tam giác AOB. Do hai cạnh OA và OB bằng nhau (là bán kính), và cung AB ứng với góc 60° tại tâm (vì một vòng tròn là 360° chia đều cho 6 phần), nên tam giác AOB cân tại O.

Từ đó suy ra AB = BC = CD = DE = EF = FA, chứng tỏ đây là hình lục giác đều. Có thể tham khảo thêm cách chứng minh 4 điểm cùng thuộc một đường tròn để hiểu sâu hơn về các điều kiện điểm thuộc đường tròn.

Ứng dụng trong bài toán hình học

Tính chất của hình lục giác đều nội tiếp đường tròn được ứng dụng rộng rãi trong nhiều bài toán hình học. Đặc biệt trong việc tính toán diện tích và chu vi của hình lục giác đều khi biết bán kính đường tròn ngoại tiếp.

Trong thực tế, cấu trúc này thường xuất hiện trong thiết kế kiến trúc và mỹ thuật. Ví dụ như trong thiết kế các công trình có mặt bằng hình lục giác, hay trong thiết kế logo công ty với hình lục giác đều làm nền tảng.

Ngoài ra, tính chất này còn được ứng dụng trong việc chia đều một đường tròn thành 6 phần bằng nhau, một kỹ thuật thường được sử dụng trong công nghiệp và xây dựng.

Các công thức và ứng dụng của hình lục giác đều

Hình lục giác đều là một đa giác đều có 6 cạnh bằng nhau và 6 góc bằng nhau. Chứng minh hình lục giác đều dựa trên tính chất các cạnh bằng nhau và các góc đều bằng 120 độ. Các công thức tính toán và ứng dụng của hình lục giác đều rất đa dạng trong thực tế.

Công thức tính diện tích

Diện tích hình lục giác đều được tính bằng nhiều cách khác nhau. Công thức tính diện tích hình lục giác đều phổ biến nhất là công thức sử dụng độ dài cạnh: S = (3√3/2) × a², trong đó a là độ dài cạnh.

Một cách tính khác là chia hình lục giác đều thành 6 tam giác đều bằng nhau. Diện tích mỗi tam giác được tính theo công thức (√3/4) × a², sau đó nhân với 6 để ra diện tích toàn bộ hình lục giác.

Công thức tính chu vi

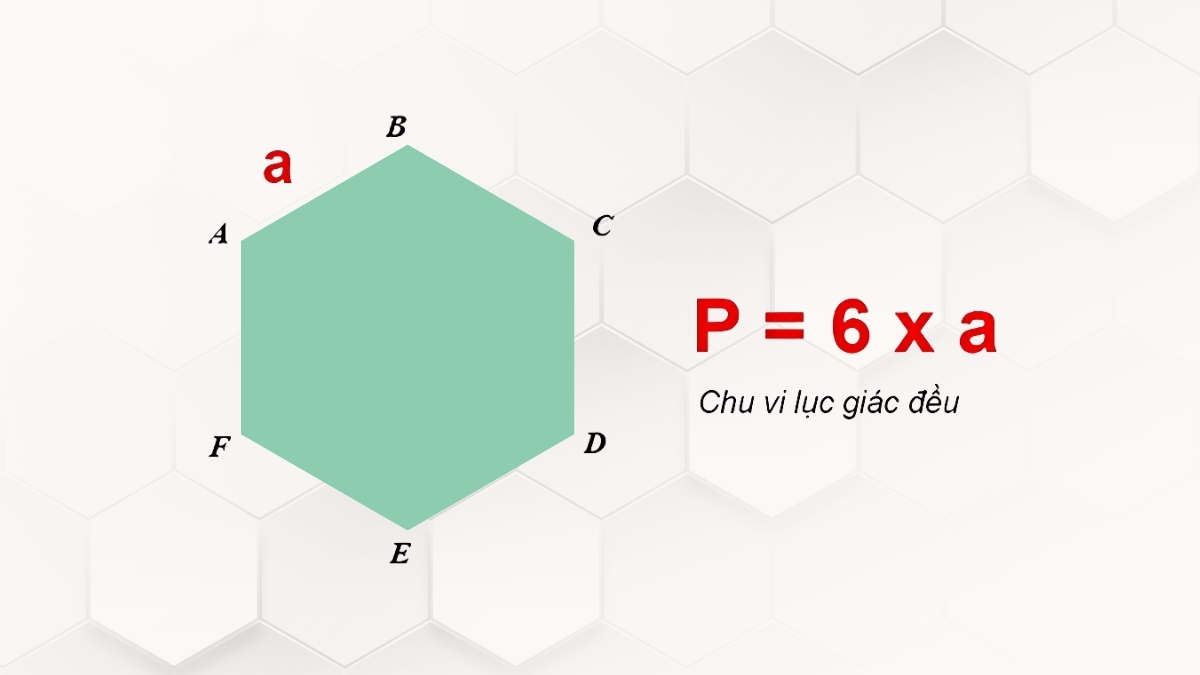
Cách tính Chu vi hình lục giác đều rất đơn giản do tính chất các cạnh bằng nhau. Chu vi được tính bằng công thức P = 6a, với a là độ dài cạnh.

Công thức này dựa trên nguyên lý cộng độ dài 6 cạnh bằng nhau. Ví dụ với hình lục giác đều có cạnh 5cm, chu vi sẽ là 30cm.

Ứng dụng trong thực tế

Hình lục giác đều xuất hiện phổ biến trong tự nhiên và kiến trúc. Tổ ong là ví dụ điển hình về cấu trúc lục giác đều trong tự nhiên, tối ưu không gian và độ bền.

Trong kiến trúc, công thức diện tích lục giác đều được ứng dụng để thiết kế gạch lát sàn, trang trí nội thất. Công ty LIXIL đã sử dụng mẫu gạch lục giác trong nhiều dự án, tạo hiệu ứng thẩm mỹ cao và tiết kiệm vật liệu.

Ngành công nghiệp sản xuất ốc vít cũng sử dụng hình dạng lục giác đều cho đầu ốc, giúp tăng độ bám và moment xoắn khi vặn. Đây là ứng dụng phổ biến trong cơ khí và xây dựng.

Chứng minh hình lục giác đều là một chủ đề thú vị trong hình học, giúp bạn hiểu sâu hơn về cấu trúc và tính chất của hình này. Việc nắm rõ các phương pháp như chứng minh sáu cạnh và góc bằng nhau, cũng như cách chứng minh hình lục giác đều nội tiếp đường tròn sẽ tạo nền tảng vững chắc cho bạn trong các bài toán hình học. Hãy áp dụng các kiến thức đã học vào thực tế để cải thiện kỹ năng giải toán của mình!