Đường chéo hình lục giác đều: Khái niệm, tính chất và cách tính toán chi tiết

Đường chéo hình lục giác đều là những đoạn thẳng nối hai đỉnh không liền kề của hình lục giác đều. Tìm hiểu về số lượng, cách tính và ứng dụng của các đường chéo sẽ giúp bạn nắm vững kiến thức hình học. Bên cạnh đó, phân tích các tính chất đặc trưng của hình lục giác đều cũng sẽ mở ra nhiều khía cạnh thú vị trong toán học.

Đường chéo hình lục giác đều là các đoạn thẳng nối hai đỉnh không liền kề của hình lục giác đều

Đường chéo hình lục giác đều là những đoạn thẳng nối hai đỉnh không liền kề của hình lục giác đều. Trong một lục giác đều, mỗi đỉnh có thể nối với 3 đỉnh không liền kề khác, tạo thành 9 đường chéo khác nhau.

Các đường chéo của hình lục giác đều có những tính chất đặc biệt. Chúng tạo thành 3 cặp đường chéo song song và bằng nhau. Điểm giao nhau của các đường chéo nằm trên đường tròn nội tiếp của hình lục giác đều.

Độ dài của các đường chéo trong hình lục giác đều có mối liên hệ với cạnh của hình. Nếu gọi a là độ dài cạnh của hình lục giác đều, các đường chéo ngắn nhất có độ dài bằng a√3, các đường chéo dài nhất có độ dài bằng 2a. Đây là những tỷ lệ quan trọng thường được sử dụng trong các bài toán hình học.

Trong thực tế, các đường chéo của hình lục giác đều đóng vai trò quan trọng trong nhiều ứng dụng. Chẳng hạn như trong thiết kế kiến trúc, các đường chéo giúp tạo nên sự cân đối và ổn định cho công trình. Trong thiết kế logo, đường chéo lục giác đều thường được sử dụng để tạo hiệu ứng thị giác ấn tượng.

Các tính chất quan trọng của đường chéo trong hình lục giác đều

Đường chéo hình lục giác đều là những đoạn thẳng nối hai đỉnh không liền kề của hình. Các đường chéo đóng vai trò quan trọng trong việc phân chia và xác định các yếu tố hình học của hình lục giác đều. Để hiểu rõ hơn về đặc điểm và tính chất của chúng, ta cần xem xét các khía cạnh sau:

Số lượng và cách xác định đường chéo hình lục giác đều

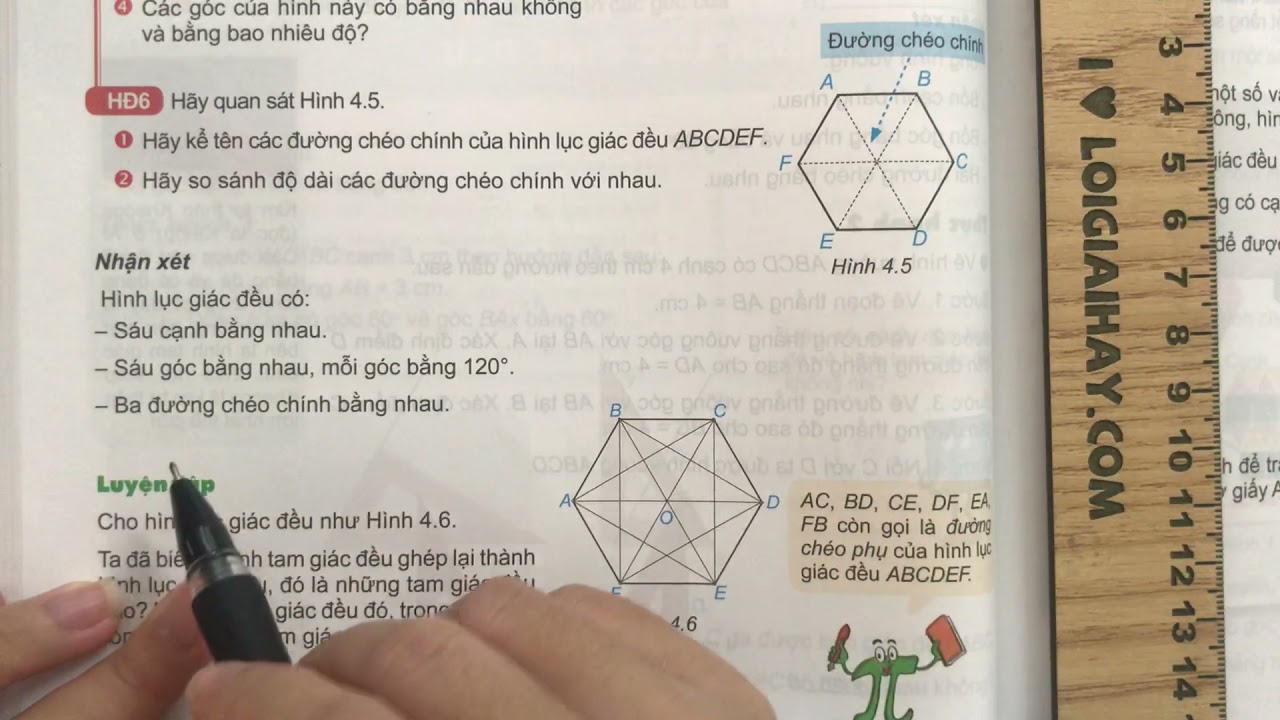
Một hình lục giác đều có tổng cộng 9 đường chéo. Cách tính số đường chéo của đa giác được thực hiện dựa trên công thức n(n-3)/2, trong đó n là số cạnh của đa giác. Với hình lục giác, n = 6, nên số đường chéo là 6(6-3)/2 = 9.

Các đường chéo được xác định bằng cách nối các đỉnh không liền kề với nhau. Số đường chéo chính của hình lục giác đều là 3, đó là những đường chéo đi qua tâm của hình và chia hình thành các phần bằng nhau.

Đặc điểm của đường chéo trong hình lục giác đều

Các đường chéo trong hình lục giác đều có những đặc điểm độc đáo. Chúng tạo thành các tam giác đều và tam giác cân khi cắt nhau. Đường chéo chính luôn đi qua tâm và vuông góc với nhau, tạo thành góc 60 độ.

Khi các đường chéo cắt nhau, chúng tạo ra các điểm giao nhau đặc biệt. Những điểm này chia đường chéo theo tỷ lệ nhất định và có thể sử dụng để xác định các yếu tố khác của hình lục giác đều.

Mối quan hệ giữa đường chéo và cạnh của hình lục giác đều

Đường chéo và cạnh của hình lục giác đều có mối quan hệ chặt chẽ về độ dài. Độ dài đường chéo ngắn nhất bằng 2 lần cạnh của hình lục giác đều. Đường chéo dài nhất (đường chéo chính) bằng 2 lần cạnh nhân với căn bậc hai của 3.

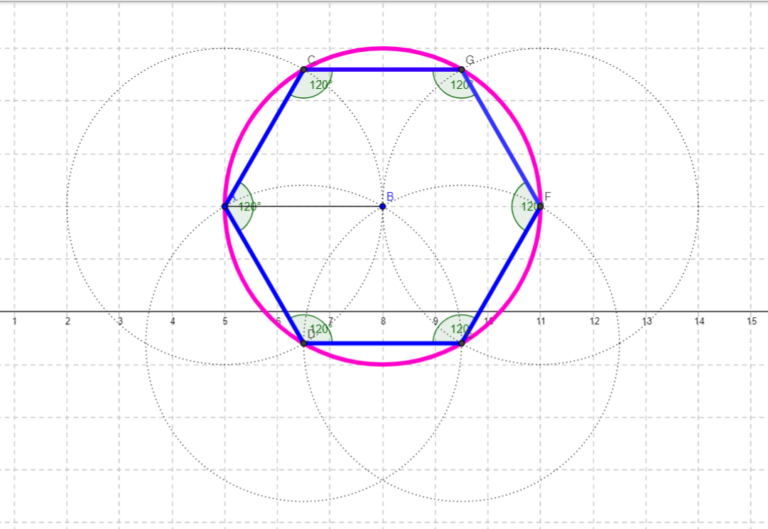
Các đường chéo tạo với cạnh những góc đặc biệt. Góc giữa đường chéo và cạnh liền kề luôn là bội số của 30 độ. Hình lục giác đều có bao nhiêu đường chéo phụ thuộc vào số đỉnh của nó, và các đường chéo này tạo nên một mạng lưới đối xứng hoàn hảo.

Phương pháp tính toán và ứng dụng của đường chéo hình lục giác đều

Trong hình học phẳng, đường chéo hình lục giác đều đóng vai trò quan trọng giúp tính toán các yếu tố khác của hình. Để tính toán chính xác các đường chéo, cần nắm vững các công thức và phương pháp xác định góc. cách chứng minh hình lục giác đều sẽ giúp hiểu rõ hơn về các tính chất của hình trước khi đi vào tính toán chi tiết.

Công thức tính độ dài đường chéo hình lục giác đều

Cách tính đường chéo hình lục giác đều dựa trên mối quan hệ với cạnh của hình. Khi biết độ dài cạnh a, độ dài đường chéo d được tính theo công thức: d = a√3, trong đó a là độ dài cạnh.

Công thức này xuất phát từ việc đường chéo chia hình lục giác đều thành các tam giác đều. Mỗi tam giác đều có cạnh bằng cạnh của hình lục giác ban đầu, và đường cao của tam giác chính là nửa đường chéo cần tìm.

Cách xác định góc giữa các đường chéo

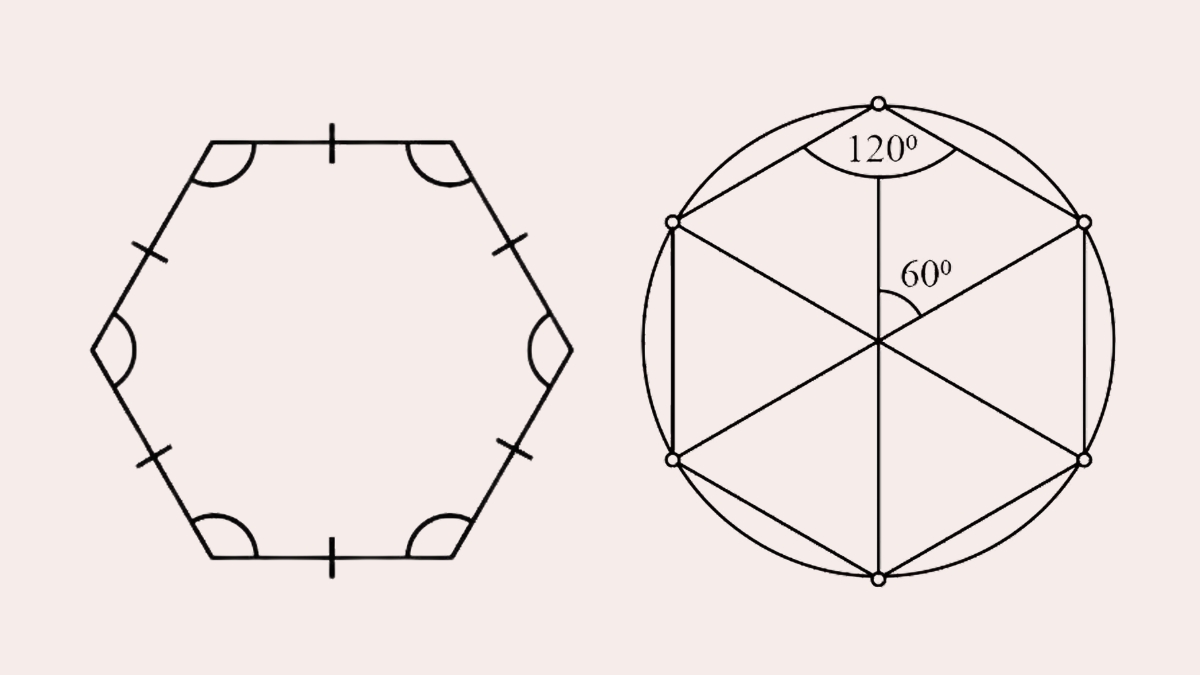
Góc giữa các đường chéo trong hình lục giác đều được xác định dựa trên tính chất đối xứng. Các đường chéo tạo với nhau góc 60° khi đi qua tâm hình lục giác.

Khi vẽ tất cả các đường chéo, chúng tạo thành 6 tam giác đều nhỏ bên trong hình lục giác. Điều này giúp dễ dàng xác định các góc giữa các đường chéo liên tiếp luôn bằng 60°.

Ứng dụng đường chéo trong tính diện tích hình lục giác đều

Công thức đường chéo lục giác giúp tính diện tích hình theo nhiều cách khác nhau. Phương pháp phổ biến là chia hình thành 6 tam giác đều bằng nhau bởi các đường chéo.

Diện tích hình lục giác đều bằng tổng diện tích 6 tam giác đều được tạo bởi các đường chéo. Mỗi tam giác có cạnh bằng cạnh của hình lục giác ban đầu, từ đó dễ dàng tính được diện tích tổng thể.

Ngoài ra, đường chéo còn được ứng dụng để xác định tâm đối xứng và vẽ đường tròn ngoại tiếp, nội tiếp hình lục giác đều.

So sánh đường chéo hình lục giác đều với các hình học khác

Khi nghiên cứu về đường chéo hình lục giác, ta thấy có nhiều điểm khác biệt so với các hình học khác. Trong hình lục giác đều, các đường chéo tạo thành một mạng lưới đối xứng, chia hình thành các tam giác đều bằng nhau.

Đặc điểm nổi bật của hình lục giác đều là có 9 đường chéo, trong khi các hình học khác như tam giác không có đường chéo, tứ giác có 2 đường chéo. Điều này tạo nên sự phức tạp và đa dạng trong cấu trúc hình học của lục giác đều.

Đường chéo trong hình lục giác đều và hình tam giác

So với đường chéo hình tam giác cân, đường chéo trong hình lục giác đều có số lượng và tính chất hoàn toàn khác biệt. Các đường chéo trong hình lục giác đều tạo thành các góc bằng nhau khi cắt nhau tại tâm hình.

Một điểm đặc biệt là các đường chéo trong hình lục giác đều chia hình thành 6 tam giác đều bằng nhau, có chung đỉnh tại tâm. Điều này tạo nên tính đối xứng hoàn hảo mà không phải hình nào cũng có được.

Sự khác biệt với đường chéo trong hình chóp và hình lập phương

So với đường chéo của hình lập phương, đường chéo trong hình lục giác đều nằm trên cùng một mặt phẳng. Trong khi đó, đường chéo hình lập phương tạo thành các đường xiên trong không gian ba chiều.

Hình chóp tứ giác đều có đường chéo đáy và đường cao, tạo thành cấu trúc không gian phức tạp hơn. Ngược lại, đường chéo trong hình lục giác đều chỉ tồn tại trên mặt phẳng và có tính chất đối xứng cao hơn.

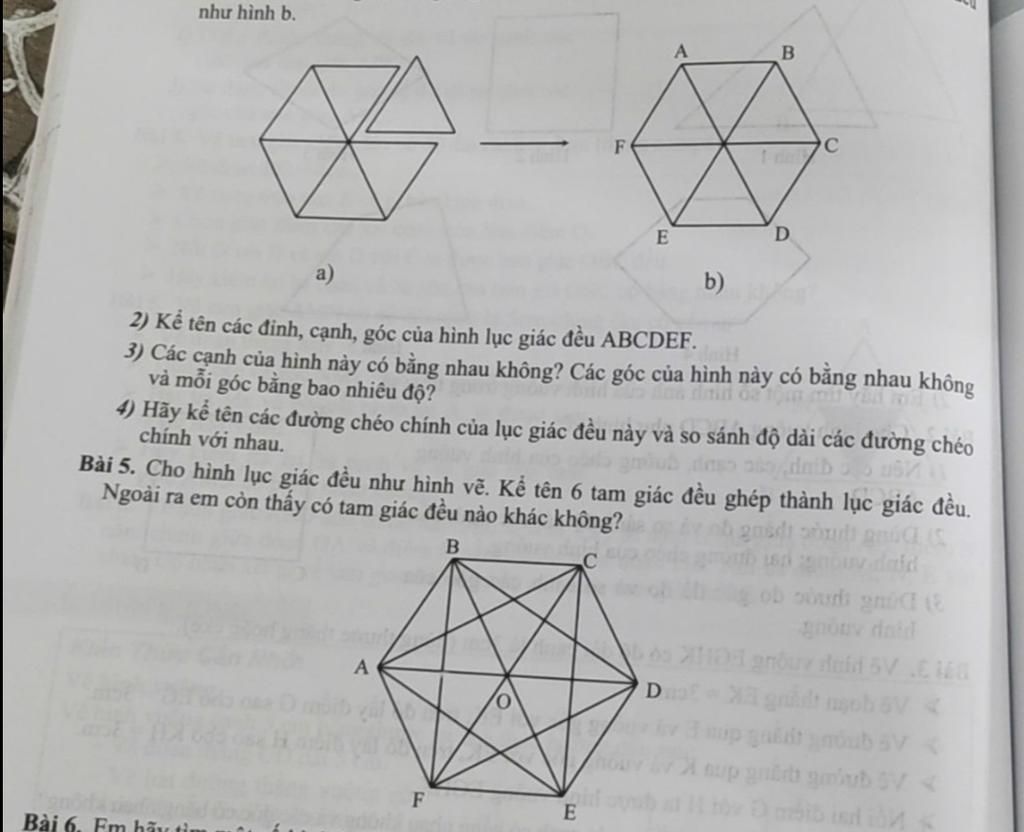
Các đường chéo trong hình lục giác đều còn có đặc điểm là bằng nhau về độ dài, trong khi đường chéo của hình chóp và hình lập phương có thể khác nhau tùy thuộc vào kích thước các cạnh và chiều cao.

Bài tập và phương pháp giải về đường chéo hình lục giác đều

Đường chéo hình lục giác đều là một yếu tố quan trọng giúp giải quyết nhiều bài toán hình học phức tạp. Việc nắm vững các tính chất và phương pháp tính toán liên quan đến đường chéo sẽ giúp học sinh giải nhanh và chính xác các dạng bài tập.

Để tính diện tích lục giác, ta thường sử dụng đường chéo để chia thành các tam giác bằng nhau. Phương pháp này giúp đơn giản hóa quá trình tính toán và kiểm chứng kết quả một cách hiệu quả.

Các dạng bài tập thường gặp

Trong quá trình học tập, học sinh thường gặp các bài toán về tính năng lục giác thông qua việc sử dụng đường chéo. Các dạng bài tập phổ biến bao gồm tính độ dài đường chéo, tìm góc giữa các đường chéo và tính diện tích các phần được tạo bởi đường chéo.

Một số bài toán yêu cầu ứng dụng lục giác vào thực tế như thiết kế mẫu hình học, trang trí nội thất hay giải quyết các vấn đề về kiến trúc. Những bài toán này đòi hỏi sự linh hoạt trong việc áp dụng kiến thức về đường chéo.

Phương pháp giải và mẹo làm bài

Khi giải các bài toán về đường chéo, việc phân loại lục giác theo đặc điểm và tính chất là bước đầu tiên quan trọng. Điều này giúp xác định chính xác công thức và phương pháp giải phù hợp.

Một mẹo hữu ích là vẽ hình phụ và sử dụng tính chất đối xứng của lục giác đều. Việc này giúp rút ngắn thời gian giải và tránh sai sót trong quá trình tính toán.

Ngoài ra, việc ghi nhớ các công thức cơ bản về đường chéo và mối quan hệ với cạnh của lục giác đều sẽ giúp giải nhanh nhiều dạng bài tập phức tạp.

Bài tập minh họa có lời giải chi tiết

Bài toán: Cho lục giác đều ABCDEF cạnh a. Tính độ dài đường chéo AD và diện tích hình lục giác.

Lời giải:

• Bước 1: Xác định đường chéo AD là đường nối 2 đỉnh đối diện
• Bước 2: Áp dụng công thức: AD = 2a
• Bước 3: Tính diện tích: S = (3√3/2)a²

Một ví dụ khác về ứng dụng thực tế: Công ty kiến trúc XYZ đã sử dụng hình lục giác đều trong thiết kế trần nhà, với các đường chéo tạo thành họa tiết độc đáo. Dự án này đã chứng minh giá trị thẩm mỹ và tính ứng dụng cao của lục giác đều trong kiến trúc hiện đại.

Trong toán học, đường chéo hình lục giác đều là một khái niệm quan trọng giúp hiểu rõ hơn về cấu trúc của hình này. Bằng cách tìm hiểu số lượng, đặc điểm và cách tính toán các đường chéo, bạn sẽ nắm vững kiến thức cần thiết để giải bài tập liên quan. Việc ứng dụng những kiến thức này không chỉ giúp bạn tự tin hơn trong học tập mà còn phát huy khả năng tư duy logic trong toán học.