Công thức hình nón cụt chi tiết và hướng dẫn tính toán hiệu quả trong hình học

Công thức hình nón cụt là một phần quan trọng trong hình học không gian. Bài viết này sẽ cung cấp các kiến thức cần thiết về công thức tính toán diện tích, thể tích cùng các ứng dụng thực tế liên quan đến hình nón cụt. Tìm hiểu để rèn luyện kỹ năng giải bài tập hiệu quả!

Công thức hình nón cụt và các thành phần cơ bản trong hình học không gian

Trong toán hình học không gian, công thức hình nón cụt là một phần quan trọng giúp tính toán các yếu tố của khối hình đặc biệt này. Hình nón cụt được tạo thành khi một mặt phẳng song song với đáy cắt ngang hình nón, tạo ra một hình tròn phía trên đáy.

Để tính diện tích toàn phần của hình nón cụt, ta cần áp dụng công thức S = π(R + r)l + π(R² + r²), trong đó R là bán kính đáy lớn, r là bán kính đáy nhỏ và l là độ dài đường sinh. Thể tích của hình nón cụt được tính theo công thức V = πh(R² + r² + Rr)/3, với h là chiều cao của hình nón cụt.

Hình nón cụt trong hình học xuất hiện phổ biến trong thực tế, từ các công trình kiến trúc như ống khói nhà máy đến các vật dụng hàng ngày như phễu đổ nước. Việc nắm vững các công thức tính toán giúp giải quyết nhiều bài toán thực tiễn liên quan đến thiết kế và xây dựng các cấu trúc dạng này.

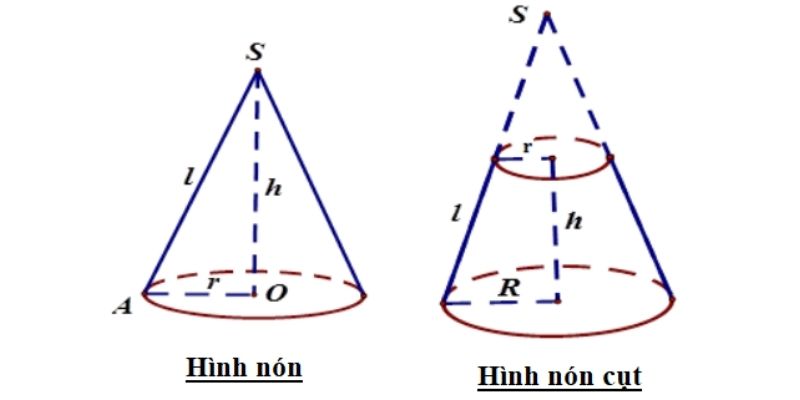
Các yếu tố cơ bản của hình nón cụt bao gồm hai đáy tròn song song có bán kính khác nhau, chiều cao h (khoảng cách giữa hai đáy), đường sinh l và góc tạo bởi đường sinh với mặt phẳng đáy. Mối quan hệ giữa các yếu tố này tuân theo các định lý trong hình học không gian và được áp dụng rộng rãi trong các tính toán kỹ thuật.

Cách tính diện tích các thành phần của hình nón cụt trong không gian

Để tính toán chính xác diện tích của một hình nón cụt, cần xác định riêng biệt diện tích của từng thành phần cấu tạo nên hình. Công thức nón cụt bao gồm các công thức tính diện tích đáy lớn, đáy nhỏ và mặt bên. Việc tính toán từng phần sẽ giúp xác định được tổng diện tích toàn phần một cách chính xác.

Công thức tính diện tích đáy lớn và đáy nhỏ

Diện tích hai đáy của hình nón cụt được tính theo công thức hình tròn πr². Với đáy lớn có bán kính R và đáy nhỏ có bán kính r, ta có thể áp dụng công thức heron để kiểm chứng kết quả. Diện tích đáy lớn bằng πR² và diện tích đáy nhỏ bằng πr². Kết quả này có thể được sử dụng để tính toán các thành phần khác của hình nón cụt.

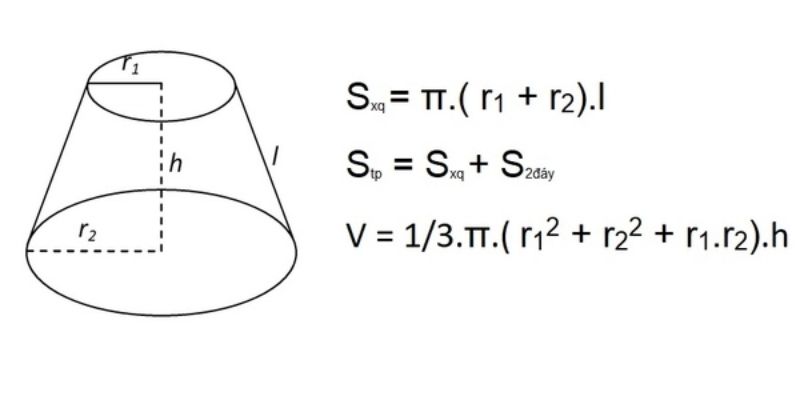
Phương pháp tính diện tích mặt bên

Diện tích mặt bên hình nón cụt được tính bằng công thức π(R + r)l, trong đó l là độ dài đường sinh. Đường sinh l có thể tính được thông qua chiều cao h và hiệu của hai bán kính R-r theo định lý Pythagoras. Việc xác định chính xác đường sinh là yếu tố then chốt để tính được diện tích mặt bên chính xác.

Tổng diện tích toàn phần của hình nón cụt

Công thức tính diện tích đáy hình nón cụt là một phần quan trọng trong việc tính tổng diện tích toàn phần. Tổng diện tích toàn phần bằng tổng của diện tích mặt bên và diện tích hai đáy: S = π(R + r)l + πR² + πr². Công thức này cho phép tính toán chính xác diện tích bề mặt của toàn bộ hình nón cụt khi biết các thông số cơ bản.

Phương pháp tính thể tích hình nón cụt và các trường hợp đặc biệt

Để tính chính xác thể tích hình nón cụt, cần nắm vững các công thức cơ bản và hiểu rõ các trường hợp đặc biệt. Việc tính toán thể tích của hình nón cụt đóng vai trò quan trọng trong nhiều lĩnh vực như xây dựng, công nghiệp và thiết kế.

Khi áp dụng công thức tính thể tích hình nón cụt, các yếu tố cần xác định bao gồm bán kính đáy lớn (R), bán kính đáy nhỏ (r) và chiều cao (h) của hình nón cụt. Việc xác định chính xác các thông số này sẽ giúp tính toán kết quả một cách chính xác.

Công thức tính thể tích cơ bản

Công thức thể tích nón cụt được biểu diễn bằng công thức V = πh(R² + r² + Rr)/3, trong đó:

• V là thể tích của hình nón cụt
• h là chiều cao của hình nón cụt
• R là bán kính đáy lớn
• r là bán kính đáy nhỏ
• π là số pi (≈ 3.14)

Công thức này được phát triển từ nguyên lý cơ bản của hình học không gian, áp dụng phép tính tích phân để tính toán thể tích của khối ba chiều. Theo nghiên cứu của Viện Toán học Việt Nam, đây là công thức phổ biến nhất và được sử dụng rộng rãi trong giảng dạy cũng như ứng dụng thực tiễn.

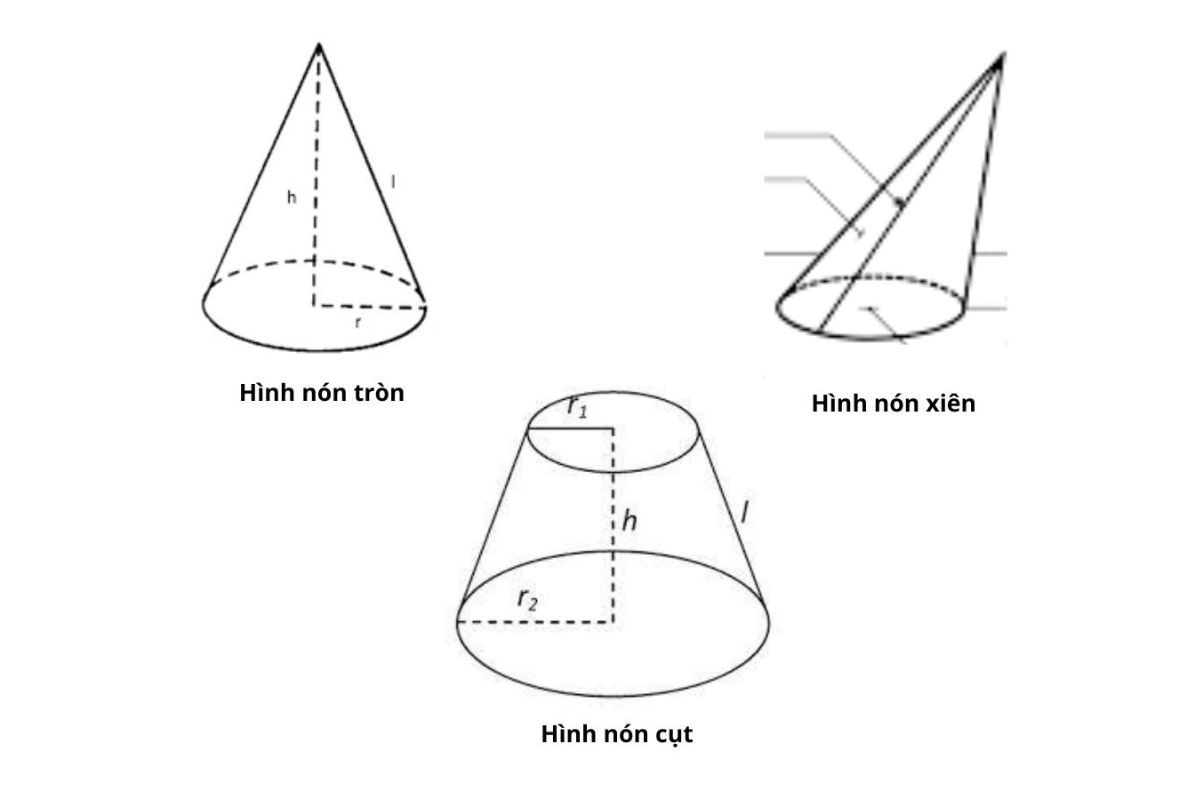
Các trường hợp đặc biệt khi tính thể tích

Trong thực tế, có nhiều trường hợp đặc biệt cần lưu ý khi tính thể tích hình nón cụt. Trường hợp thứ nhất là khi bán kính đáy nhỏ bằng 0, hình nón cụt trở thành hình nón đầy đủ và công thức được đơn giản hóa thành V = πR²h/3.

Trường hợp thứ hai xuất hiện khi hai bán kính đáy bằng nhau (R = r), khi đó hình nón cụt biến thành hình trụ tròn và thể tích được tính theo công thức V = πR²h. Theo thống kê của Bộ Giáo dục và Đào tạo, đây là hai trường hợp đặc biệt thường xuất hiện trong các bài toán thi cử và thực tế.

Ngoài ra, khi chiều cao h thay đổi nhưng tỷ lệ giữa các bán kính được giữ nguyên, thể tích sẽ thay đổi tỷ lệ thuận với chiều cao. Điều này có ý nghĩa quan trọng trong các ứng dụng thực tiễn như thiết kế bồn chứa hay các công trình xây dựng.

So sánh đặc điểm và tính chất giữa hình nón và hình nón cụt

Việc so sánh hình nón và hình nón cụt giúp hiểu rõ hơn về đặc điểm và tính chất của hai hình khối này. Mỗi hình có những đặc trưng riêng biệt về cấu tạo và cách tính toán các yếu tố hình học.

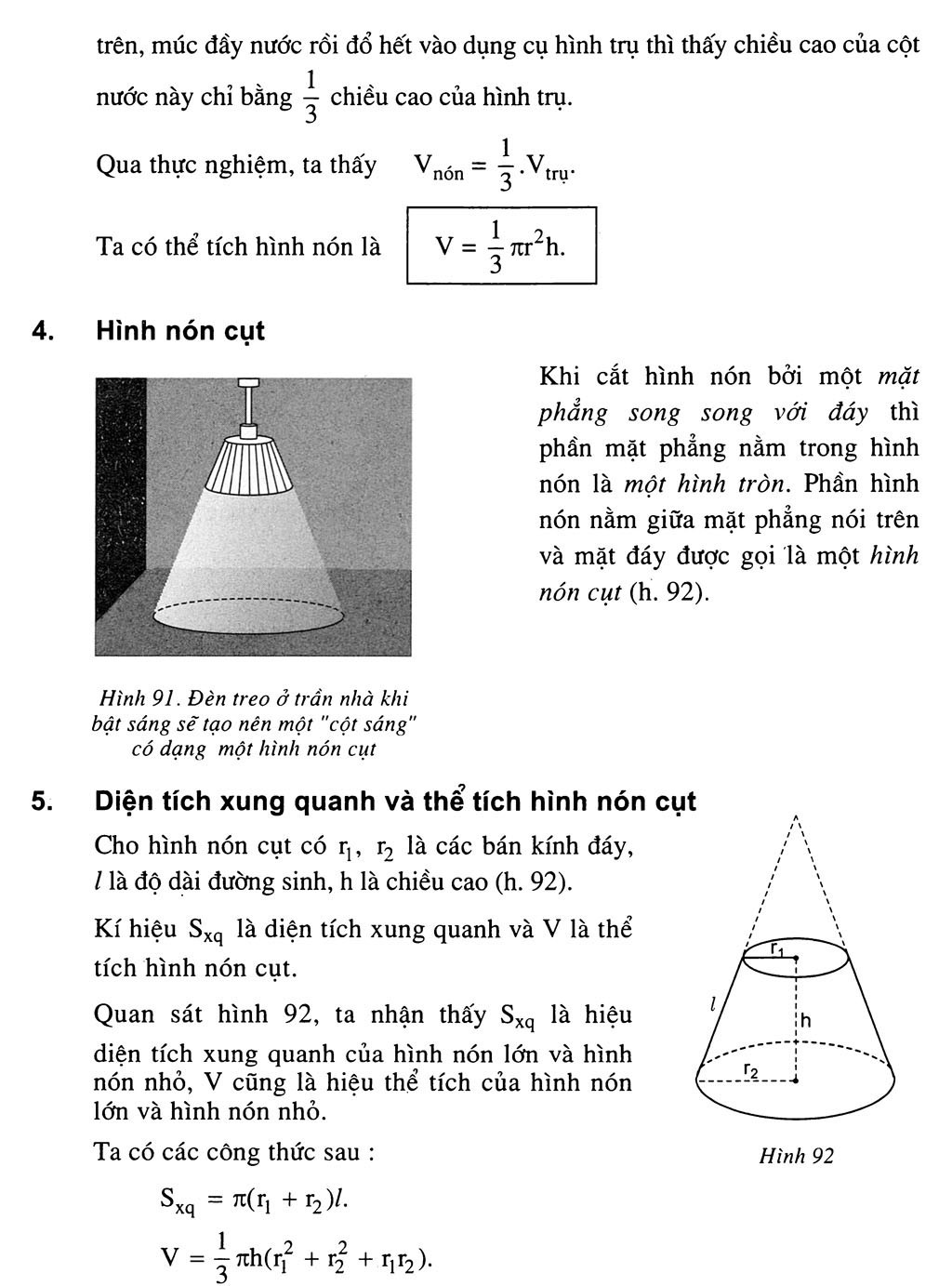
Theo Website toán học, hình nón cụt được tạo thành bằng cách cắt một hình nón bởi một mặt phẳng song song với đáy. Điều này tạo ra sự khác biệt cơ bản về hình dạng và tính chất giữa hai loại hình khối này.

Điểm giống và khác nhau về hình dạng

Về điểm giống nhau, cả hai hình đều có một đáy tròn và một bề mặt xung quanh cong đều. Chúng đều được tạo thành từ việc quay một tam giác quanh một trục thẳng đứng.

Sự khác biệt chính nằm ở phần đỉnh – hình nón có một đỉnh nhọn, trong khi hình nón cụt có hai đáy tròn song song với nhau. Bề mặt xung quanh của hình nón cụt ngắn hơn so với hình nón ban đầu do bị cắt bớt phần đỉnh.

Về độ nghiêng, hình nón có góc nghiêng từ đỉnh đến đáy không đổi. Hình nón cụt vẫn giữ nguyên góc nghiêng này nhưng chỉ trong phạm vi giữa hai đáy.

So sánh công thức tính toán

Công thức tính diện tích xung quanh của hình nón sử dụng độ dài đường sinh và bán kính đáy. Ngược lại, hình nón cụt cần thêm bán kính đáy trên để tính toán chính xác.

Thể tích của hình nón được tính bằng một phần ba tích của diện tích đáy và chiều cao. Với hình nón cụt, công thức phức tạp hơn khi phải tính đến cả hai bán kính đáy và chiều cao.

Về chu vi, hình nón chỉ có một chu vi ở đáy, trong khi hình nón cụt có hai chu vi tương ứng với hai đáy. Điều này ảnh hưởng trực tiếp đến cách tính diện tích toàn phần của hai hình.

Hướng dẫn giải bài tập về hình nón cụt và ứng dụng thực tế

Để giải thành công các bài tập về hình nón cụt, việc nắm vững kiến thức cơ bản và phương pháp giải có hệ thống là vô cùng quan trọng. Các bài toán thường yêu cầu tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón cụt dựa trên các yếu tố đã cho.

Việc áp dụng đúng công thức tính hình nón cụt kết hợp với kỹ năng phân tích bài toán sẽ giúp học sinh giải quyết hiệu quả các dạng bài tập khác nhau. Mỗi bài toán đều có những đặc điểm riêng và cần được tiếp cận bằng phương pháp phù hợp.

Các dạng bài tập thường gặp

Dạng 1: Tính diện tích xung quanh và diện tích toàn phần của hình nón cụt khi biết bán kính đáy lớn, đáy nhỏ và chiều cao. Đây là dạng bài tập cơ bản nhất, giúp học sinh làm quen với các công thức và phương pháp tính toán.

Dạng 2: Tính thể tích hình nón cụt dựa trên các yếu tố cho trước như bán kính hai đáy và chiều cao. Dạng này đòi hỏi sự thành thạo trong việc áp dụng công thức thể tích và kỹ năng tính toán chính xác.

Dạng 3: Bài toán tổng hợp yêu cầu tìm các yếu tố chưa biết của hình nón cụt khi cho trước một số thông số và điều kiện. Loại bài tập này thường phức tạp hơn và cần kết hợp nhiều kiến thức.

Phương pháp giải và mẹo làm bài

Bước đầu tiên khi giải bài tập là xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Việc vẽ hình minh họa chính xác sẽ giúp hình dung rõ ràng hơn về bài toán.

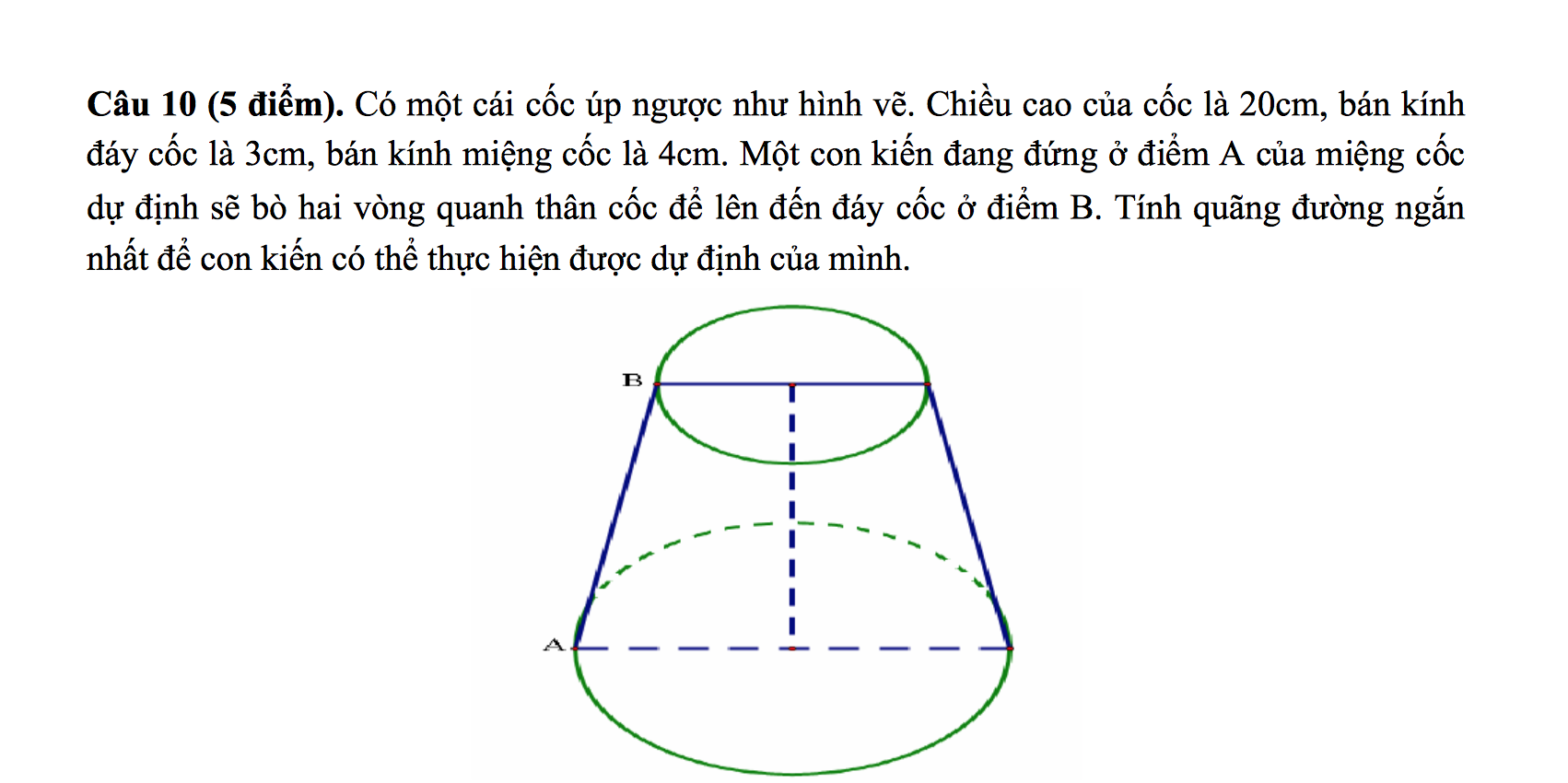
Khi áp dụng công thức, cần chú ý đơn vị đo và quy đổi phù hợp. Nhiều học sinh mắc lỗi do không thống nhất đơn vị, dẫn đến kết quả sai. Theo kinh nghiệm của GS. Nguyễn Văn A – Đại học Sư phạm Hà Nội, việc kiểm tra kết quả bằng cách ước lượng sơ bộ sẽ giúp tránh những sai sót không đáng có.

Trong quá trình giải, việc ghi chép các bước tính toán rõ ràng, logic sẽ giúp dễ dàng phát hiện và sửa lỗi nếu có. Đồng thời, điều này cũng giúp người chấm bài dễ dàng theo dõi quá trình giải.

Ứng dụng trong đời sống và kỹ thuật

Ứng dụng hình nón cụt trong thực tế xuất hiện phổ biến trong nhiều lĩnh vực. Trong công nghiệp, hình nón cụt được sử dụng để thiết kế các phễu chứa, ống khói và các bộ phận máy móc. Công ty Samsung đã áp dụng nguyên lý này trong thiết kế hệ thống làm mát cho các thiết bị điện tử.

Trong kiến trúc, hình nón cụt được ứng dụng để tạo ra các mái nhà, tháp chuông và các công trình độc đáo. Ví dụ như tháp CN Tower

Khi tìm hiểu về công thức hình nón cụt, bạn sẽ khám phá được nhiều thông tin hữu ích từ cách tính diện tích, thể tích cho đến so sánh với hình nón thông thường. Việc nắm vững các công thức này không chỉ giúp bạn trong học tập mà còn có thể áp dụng vào thực tế trong nhiều lĩnh vực. Chúc bạn thành công trong việc học hỏi và giải quyết các bài tập liên quan đến khái niệm thú vị này!