Tìm hiểu 3 vecto đồng phẳng và các phương pháp tính toán trong không gian

3 vecto đồng phẳng là một chủ đề quan trọng trong hình học và đại số tuyến tính. Hiểu rõ về điều kiện và tính chất của chúng giúp người học giải quyết hiệu quả các bài toán liên quan đến mặt phẳng trong không gian. Tìm hiểu những quy tắc và ứng dụng của chúng mang lại nhiều kiến thức bổ ích trong quá trình học toán.

Tìm hiểu về 3 vecto đồng phẳng và các điều kiện cần thiết trong không gian

Ba vecto đồng phẳng là các vecto nằm trên cùng một mặt phẳng trong không gian ba chiều. Điều này có nghĩa là chúng có thể biểu diễn được dưới dạng tổ hợp tuyến tính của hai vecto không cùng phương bất kỳ nằm trên mặt phẳng đó.

Trong hình học vector toán học, để xác định ba vecto có đồng phẳng hay không, ta cần kiểm tra tích hỗn tạp của chúng. Cụ thể, ba vecto a, b và c đồng phẳng khi và chỉ khi tích hỗn tạp [a b c] = 0. Điều kiện này tương đương với việc một trong ba vecto có thể biểu diễn được qua hai vecto còn lại.

Một ví dụ thực tế về ba vecto đồng phẳng là khi xét chuyển động của một vật trên mặt phẳng nghiêng. Vecto vận tốc, vecto gia tốc và vecto trọng lực đều nằm trên cùng một mặt phẳng. Tương tự như hai vecto cùng phương, việc xác định các vecto đồng phẳng giúp đơn giản hóa nhiều bài toán trong vật lý và kỹ thuật.

Trong thực tế, việc xác định các vecto đồng phẳng còn được ứng dụng rộng rãi trong đồ họa máy tính, thiết kế 3D và robot học. Ví dụ, khi lập trình chuyển động cho cánh tay robot, việc đảm bảo các vecto chuyển động nằm trên cùng một mặt phẳng giúp kiểm soát chính xác quỹ đạo và tránh va chạm với các vật cản.

Điều kiện để 3 vecto trở thành vecto đồng phẳng trong không gian ba chiều

Ba vecto trong không gian ba chiều sẽ trở thành 3 vecto đồng phẳng khi chúng nằm trên cùng một mặt phẳng. Điều này xảy ra khi một trong các vecto có thể biểu diễn được thành tổ hợp tuyến tính của hai vecto còn lại. Tương tự như tính chất tam giác đồng dạng, các vecto đồng phẳng cũng tuân theo các quy luật về tỷ lệ và góc.

Về mặt đại số, điều kiện để 3 vecto đồng phẳng được thể hiện thông qua định thức của ma trận tạo bởi tọa độ của chúng bằng 0. Điều này phản ánh sự phụ thuộc tuyến tính giữa các vecto.

Định nghĩa và tính chất cơ bản của vecto đồng phẳng

Vecto đồng phẳng là các vecto nằm trên cùng một mặt phẳng trong không gian ba chiều. Khi xét về góc, các vecto này tạo thành một hệ phẳng, nghĩa là không có vecto nào “nhô” ra khỏi mặt phẳng chứa hai vecto còn lại.

Tính chất quan trọng nhất của vecto đồng phẳng là tích hỗn hợp của chúng luôn bằng 0. Điều này có nghĩa thể tích của hình hộp chỉ phương được tạo bởi ba vecto này bằng 0.

Các trường hợp đặc biệt khi 3 vecto đồng phẳng

Trường hợp đặc biệt thứ nhất là khi hai trong ba vecto song song với nhau. Lúc này vecto thứ ba có thể nằm ở bất kỳ vị trí nào trên mặt phẳng chứa hai vecto song song đó.

Trường hợp thứ hai là khi một vecto bằng tổ hợp tuyến tính của hai vecto còn lại. Ví dụ như vecto a = 2b + 3c, trong đó a, b, c là ba vecto đang xét.

Trường hợp cuối cùng là khi cả ba vecto đều song song với một đường thẳng. Đây là trường hợp suy biến nhất của vecto đồng phẳng.

Phương pháp kiểm tra 3 vecto có đồng phẳng hay không

Phương pháp đầu tiên là sử dụng tích hỗn hợp. Nếu tích hỗn hợp của ba vecto bằng 0, chúng sẽ đồng phẳng. Công thức tính dựa trên định thức của ma trận 3×3 tạo bởi tọa độ các vecto.

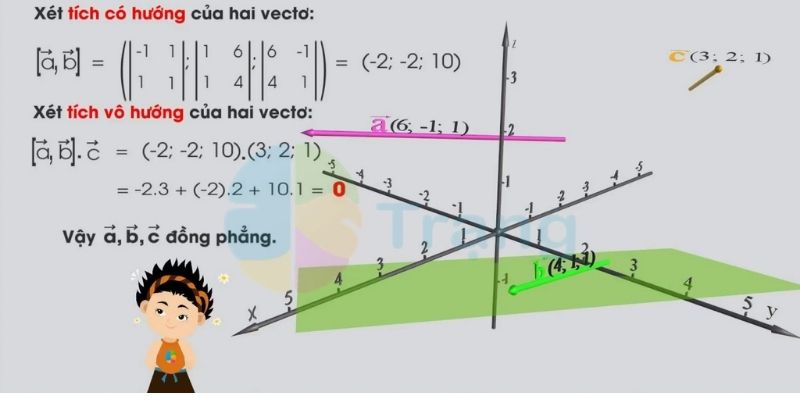
Phương pháp thứ hai là kiểm tra khả năng biểu diễn một vecto theo hai vecto còn lại. Nếu tồn tại các hệ số thực α và β sao cho a = αb + βc, thì ba vecto a, b, c đồng phẳng.

Ngoài ra, có thể sử dụng phương pháp hình học bằng cách xác định mặt phẳng chứa hai vecto bất kỳ, sau đó kiểm tra xem vecto còn lại có nằm trên mặt phẳng đó không.

Ứng dụng của 3 vecto đồng phẳng trong hình học không gian

Vector và hình học có mối liên hệ mật thiết trong việc giải quyết các bài toán hình học không gian. Ba vecto đồng phẳng đóng vai trò quan trọng trong việc xác định mặt phẳng và các yếu tố hình học liên quan.

Ứng dụng vector trong đời sống thể hiện rõ nét qua các lĩnh vực như xây dựng, kiến trúc và thiết kế 3D. Ví dụ, khi thiết kế một tòa nhà, kiến trúc sư cần xác định chính xác góc nghiêng của các mặt phẳng và vị trí tương đối giữa các cấu trúc để đảm bảo tính ổn định.

3 vecto đồng phẳng giúp xác định phương trình mặt phẳng và góc giữa các mặt phẳng, từ đó giải quyết nhiều bài toán phức tạp như ba đường conic hay tìm giao tuyến giữa các mặt phẳng.

Giải các bài toán về mặt phẳng trong không gian

Việc giải các bài toán về mặt phẳng trong không gian đòi hỏi nắm vững các phương pháp vector. Một mặt phẳng có thể được xác định bởi một điểm và hai vector chỉ phương không cùng phương, hoặc ba điểm không thẳng hàng.

Trong thực tế, các kỹ sư xây dựng thường sử dụng phương pháp này để tính toán độ nghiêng của mái nhà hoặc các cấu trúc dốc. Công ty ARUP – một tập đoàn kỹ thuật toàn cầu đã áp dụng phương pháp vector để thiết kế Nhà hát Opera Sydney với những mặt cong phức tạp.

Khi giải quyết các bài toán về mặt phẳng, cần chú ý đến tính chất song song và vuông góc của các vector để xác định chính xác vị trí và hướng của mặt phẳng trong không gian.

Xác định vị trí tương đối của đường thẳng và mặt phẳng

Xác định vị trí tương đối giữa đường thẳng và mặt phẳng là một ứng dụng quan trọng của phép tính vector. Đường thẳng và mặt phẳng có thể cắt nhau, song song hoặc đường thẳng nằm trong mặt phẳng.

Trong công nghiệp sản xuất, việc xác định chính xác góc nghiêng của các chi tiết máy đối với mặt phẳng tham chiếu là yếu tố quyết định đến độ chính xác của sản phẩm. Ví dụ, khi gia công các chi tiết trên máy CNC, góc nghiêng của dao cắt so với bề mặt gia công phải được tính toán chính xác dựa trên các vector chỉ phương.

Phương pháp vector còn được ứng dụng trong thiết kế game 3D để xác định va chạm giữa các vật thể, giúp tạo nên những trải nghiệm chơi game chân thực và mượt mà.

Phương pháp biểu diễn và tính toán với 3 vecto đồng phẳng

Việc biểu diễn và thực hiện các phép toán với vector đồng phẳng là một kỹ năng quan trọng trong hình học và đại số tuyến tính. Để nắm vững kiến thức này, cần hiểu rõ cách biểu diễn vector trong hệ tọa độ và các phép toán cơ bản. Hocthenao cung cấp phương pháp học tập hiệu quả giúp bạn làm chủ các kỹ năng tính toán vector.

Cách biểu diễn vecto trong hệ tọa độ

Khi làm việc với 3 vecto đồng phẳng, việc biểu diễn chúng trong hệ tọa độ Descartes là phương pháp phổ biến và hiệu quả nhất. Mỗi vector được xác định bởi điểm đầu và điểm cuối, với tọa độ được biểu diễn dưới dạng (x,y).

Vector có thể được biểu diễn theo nhiều cách khác nhau như dạng hình học (mũi tên có hướng), dạng tọa độ hay dạng đại số. Trong không gian hai chiều, vector thường được viết dưới dạng a = (ax,ay), trong đó ax và ay lần lượt là hoành độ và tung độ của vector.

Các phép toán cơ bản với vecto đồng phẳng

Các tính chất vector cơ bản bao gồm phép cộng, phép trừ và phép nhân với một số vô hướng. Khi thực hiện phép cộng hai vector, ta cộng các thành phần tương ứng. Ví dụ: nếu a = (x1,y1) và b = (x2,y2), thì a + b = (x1+x2, y1+y2).

Phép nhân vector với số vô hướng k được thực hiện bằng cách nhân k với từng thành phần của vector. Tích vô hướng của hai vector cho ta một số thực và được tính thông qua công thức a·b = ax×bx + ay×by.

Bài tập và ví dụ minh họa

Xét bài toán tìm diện tích tam giác được tạo bởi ba điểm A(1,2), B(3,4) và C(2,5). Ta có thể giải quyết bằng cách:

• Xác định các vector AB và AC
• Tính tích có hướng của hai vector này
• Lấy độ lớn của tích có hướng chia 2

Một ứng dụng thực tế của vector trong công nghệ đồ họa là xác định hướng chuyển động của các đối tượng trong game 2D. Các nhà phát triển sử dụng vector để tính toán vị trí, vận tốc và gia tốc của nhân vật trong game.

Các trường hợp đặc biệt và lưu ý khi làm việc với 3 vecto đồng phẳng

Khi nghiên cứu về 3 vecto đồng phẳng khi nào, ta cần hiểu rằng các vecto này phải nằm trên cùng một mặt phẳng và có thể biểu diễn thông qua tổ hợp tuyến tính. Điều kiện cơ bản là tích hỗn hợp của ba vecto bằng 0, tức là [a b c] = 0.

Việc xác định ba vectơ đồng phẳng khi nào đòi hỏi phân tích kỹ lưỡng mối quan hệ hình học giữa chúng. Các vecto này có thể có độ dài và hướng khác nhau nhưng vẫn đảm bảo nằm trên cùng một mặt phẳng.

Để xác định điều kiện 3 vecto đồng phẳng, cần kiểm tra tính phụ thuộc tuyến tính giữa chúng. Nếu một trong ba vecto có thể biểu diễn được qua tổ hợp tuyến tính của hai vecto còn lại, thì ba vecto đó chắc chắn đồng phẳng.

Trường hợp 3 vecto đồng phẳng vuông góc

Khi ba vecto đồng phẳng tạo thành ba cạnh của một tam giác vuông, chúng tạo nên một cấu trúc hình học đặc biệt. Vecto thứ nhất vuông góc với vecto thứ hai, vecto thứ hai vuông góc với vecto thứ ba.

Trong trường hợp này, tích vô hướng của hai vecto bất kỳ vuông góc với nhau sẽ bằng 0. Điều này tạo ra một hệ thống phương trình có thể giải để xác định các thành phần của vecto.

Ứng dụng thực tế của trường hợp này thường xuất hiện trong thiết kế kiến trúc và xây dựng, nơi các kết cấu vuông góc cần được tính toán chính xác để đảm bảo độ ổn định.

Trường hợp 3 vecto đồng phẳng song song

Song song là một trường hợp đặc biệt khi các vecto có cùng phương nhưng có thể có độ dài khác nhau. Trong trường hợp này, các vecto có thể biểu diễn dưới dạng tỷ lệ của nhau.

Việc xác định tính song song được thực hiện thông qua kiểm tra các thành phần tương ứng của các vecto. Nếu tỷ lệ giữa các thành phần tương ứng bằng nhau, các vecto song song.

Trong thực tế, kiến thức về vecto song song được áp dụng rộng rãi trong thiết kế đồ họa 3D và mô phỏng chuyển động, nơi cần xử lý các đối tượng chuyển động song song.

Một số sai lầm thường gặp và cách khắc phục

Sai lầm phổ biến nhất là nhầm lẫn giữa điều kiện đồng phẳng và điều kiện cộng tuyến. Nhiều người cho rằng ba vecto đồng phẳng luôn phải cộng tuyến, điều này hoàn toàn không chính xác.

Một lỗi khác là bỏ qua việc kiểm tra tích hỗn hợp khi xác định tính đồng phẳng. Tích hỗn hợp bằng 0 là điều kiện cần và đủ để ba vecto đồng phẳng.

Để tránh những sai lầm này, cần thực hiện đầy đủ các bước kiểm tra và tính toán, không nên rút gọn quá trình hay bỏ qua các bước quan trọng. Việc

Trong toán học, 3 vecto đồng phẳng là khái niệm quan trọng mà bạn cần nắm vững để giải quyết các bài toán trong hình học không gian. Việc hiểu rõ các điều kiện và tính chất của vecto đồng phẳng sẽ giúp bạn tự tin hơn khi ứng dụng vào thực tế. Hy vọng bạn sẽ áp dụng kiến thức này để nâng cao khả năng giải toán của mình một cách hiệu quả và chính xác.