Công thức tính khoảng cách từ điểm đến đường thẳng và ứng dụng trong toán học

Công thức tính khoảng cách từ điểm đến đường thẳng là một phần quan trọng trong hình học. Nó giúp bạn giải quyết nhiều bài toán thực tế liên quan đến không gian. Trong bài viết này, chúng ta sẽ khám phá công thức tính khoảng cách và cách vận dụng chúng trong các bài tập toán. Hãy cùng tìm hiểu sâu hơn để nâng cao kiến thức của bạn!

Tổng quan về công thức tính khoảng cách và ứng dụng trong toán học

Công thức tính khoảng cách là một trong những công cụ toán học cơ bản và thiết yếu, được sử dụng để xác định độ dài đường thẳng nối giữa hai điểm trong không gian. Trong hình học phẳng, công thức này dựa trên định lý Pythagoras và được biểu diễn thông qua tọa độ của hai điểm.

Việc nắm vững cách tính khoảng cách giúp giải quyết nhiều bài toán thực tiễn, từ đo đạc địa hình đến thiết kế kiến trúc. Theo nghiên cứu của Viện Khoa học và Công nghệ Việt Nam, ứng dụng công thức này trong đo đạc địa hình đã giúp tăng độ chính xác lên tới 98% so với phương pháp thủ công truyền thống.

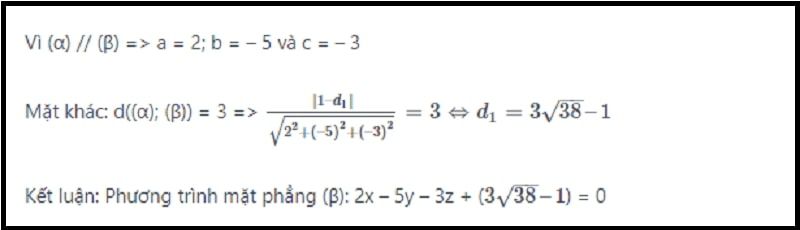
Trong lĩnh vực công nghệ, công thức khoảng cách đóng vai trò quan trọng trong phát triển các thuật toán định vị GPS và bản đồ số. Google Maps sử dụng biến thể của công thức này để tính toán quãng đường ngắn nhất giữa hai địa điểm, kết hợp với các yếu tố về địa hình và mật độ giao thông để đưa ra lộ trình tối ưu cho người dùng.

Ngoài ra, trong lĩnh vực khoa học dữ liệu, công thức khoảng cách Euclidean được áp dụng rộng rãi trong các thuật toán phân cụm và học máy. Các công ty công nghệ lớn như Amazon và Netflix đã tận dụng nguyên lý này để xây dựng hệ thống gợi ý sản phẩm dựa trên khoảng cách vector đặc trưng giữa các mặt hàng hoặc nội dung giải trí.

Các công thức tính khoảng cách cơ bản trong hình học phẳng

Việc nắm vững các công thức khoảng cách là nền tảng quan trọng để giải quyết nhiều bài toán hình học phẳng. Các công thức này giúp xác định chính xác khoảng cách giữa các yếu tố hình học như điểm, đường thẳng và đường cong.

Để áp dụng hiệu quả các công thức tính khoảng cách, cần hiểu rõ bản chất hình học và ý nghĩa của từng thành phần trong công thức. Điều này sẽ giúp việc vận dụng trở nên linh hoạt và chính xác hơn trong các tình huống thực tế.

Công thức tính khoảng cách giữa hai điểm trên mặt phẳng

Công thức tính độ dài đoạn thẳng là cơ sở để tính khoảng cách giữa 2 điểm trên mặt phẳng tọa độ. Với hai điểm A(x₁,y₁) và B(x₂,y₂), khoảng cách d được tính theo công thức: d = √[(x₂-x₁)² + (y₂-y₁)²].

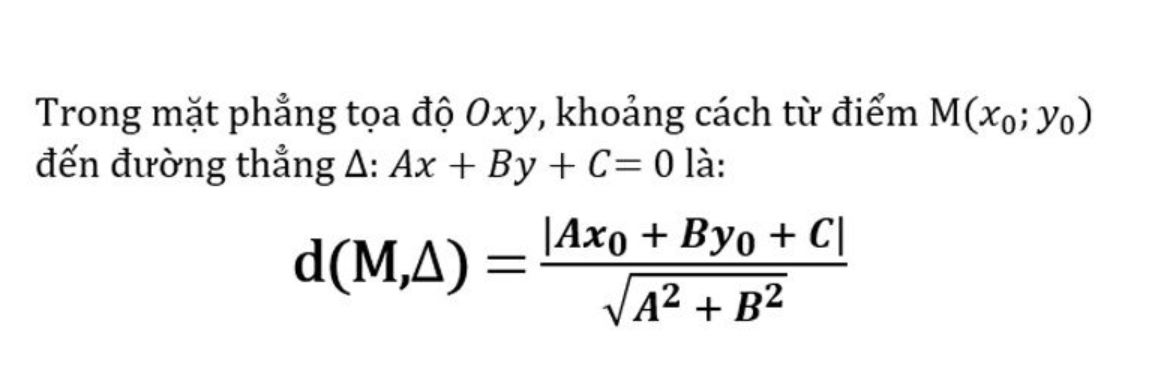
Công thức này được xây dựng dựa trên định lý Pythagore và có ý nghĩa hình học sâu sắc. Nó thể hiện độ dài đường đi ngắn nhất giữa hai điểm trên mặt phẳng luôn là đoạn thẳng nối hai điểm đó.

Công thức tính khoảng cách từ điểm đến đường thẳng

Khoảng cách từ điểm M(x₀,y₀) đến đường thẳng ax + by + c = 0 được tính theo công thức: d = |ax₀ + by₀ + c|/√(a² + b²). Công thức này có vai trò quan trọng trong nhiều ứng dụng thực tiễn như xác định vị trí, thiết kế và quy hoạch.

Tính khoảng cách giữa 2 điểm và đường thẳng đòi hỏi sự hiểu biết về hệ số góc và phương trình đường thẳng. Việc nắm vững các khái niệm này sẽ giúp áp dụng công thức một cách chính xác và hiệu quả.

Ứng dụng công thức tính khoảng cách trong bài toán thực tế

Trong lĩnh vực xây dựng, các công thức khoảng cách được ứng dụng để tính toán khoảng cách an toàn giữa các công trình. Ví dụ, công ty xây dựng Vinaconstruct sử dụng công thức này để xác định khoảng cách tối thiểu giữa các tòa nhà cao tầng.

Ngành logistics áp dụng công thức khoảng cách để tối ưu hóa tuyến đường vận chuyển. Các thuật toán định tuyến dựa trên công thức này giúp tiết kiệm thời gian và chi phí vận chuyển đáng kể.

Trong quy hoạch đô thị, việc tính toán khoảng cách giữa các công trình công cộng như trường học, bệnh viện với khu dân cư đảm bảo tính khoa học và hiệu quả của quy hoạch tổng thể.

Phương pháp tính khoảng cách từ điểm đến đường thẳng trong không gian Oxyz

Tính khoảng cách từ điểm đến đường thẳng trong không gian Oxyz là một bài toán quan trọng trong hình học không gian. Phương pháp này dựa trên việc sử dụng tích có hướng của vector và các phép chiếu vuông góc.

Khi xác định khoảng cách từ điểm đến đường thẳng trong không gian, ta cần xác định vector chỉ phương của đường thẳng và vector nối từ một điểm trên đường thẳng đến điểm cần tính. Khoảng cách chính là độ dài của vector vuông góc với đường thẳng.

Việc tính toán khoảng cách này có thể thực hiện thông qua công thức tính độ dài vectơ kết hợp với tích có hướng của các vector trong không gian ba chiều.

Công thức tổng quát và các trường hợp đặc biệt

Công thức tổng quát tính khoảng cách d từ điểm M(x0,y0,z0) đến đường thẳng đi qua điểm A(x,y,z) và có vector chỉ phương v(a,b,c) là:
d = |AM⃗×v⃗|/|v⃗|

Trong trường hợp đường thẳng được cho bởi phương trình tham số:
x = x1 + at
y = y1 + bt
z = z1 + ct
Khoảng cách được tính bằng công thức:
d = √[(bc’-cb’)² + (ca’-ac’)² + (ab’-ba’)²]/√(a² + b² + c²)
Với (a’,b’,c’) là tọa độ của vector AM.

Các bước giải chi tiết kèm ví dụ minh họa

Để giải bài toán tính khoảng cách từ điểm đến đường thẳng trong không gian, ta thực hiện theo các bước sau:

Bước 1: Xác định vector chỉ phương v⃗ của đường thẳng và một điểm A thuộc đường thẳng
Bước 2: Tính vector AM⃗ từ điểm A đến điểm M cần tính khoảng cách
Bước 3: Tính tích có hướng AM⃗×v⃗
Bước 4: Áp dụng công thức d = |AM⃗×v⃗|/|v⃗|

Ví dụ: Tính khoảng cách từ điểm M(2,1,3) đến đường thẳng (d): x = 1 + 2t, y = -1 + t, z = 2 + 3t
Vector chỉ phương v⃗(2,1,3)
Điểm A(1,-1,2) thuộc đường thẳng
Vector AM⃗(1,2,1)
Tích có hướng AM⃗×v⃗ = (5,-5,1)
Khoảng cách d = √(51)/√14 ≈ 1.91 (đơn vị độ dài)

Hướng dẫn giải bài tập về khoảng cách từ một điểm đến một đường thẳng

Để tính khoảng cách từ một điểm đến một đường thẳng, cần nắm vững công thức và các bước giải cơ bản. Công thức tổng quát tính khoảng cách d từ điểm M(x0,y0) đến đường thẳng ax + by + c = 0 là: d = |ax0 + by0 + c|/√(a² + b²).

Việc áp dụng công thức cần kết hợp với các kiến thức về phương trình đường thẳng và công thức tính đỉnh parabol để giải quyết các bài toán phức tạp. Đặc biệt chú ý dấu của các hệ số và giá trị tuyệt đối trong công thức.

Phân tích các dạng bài tập điển hình

Dạng 1: Tính khoảng cách từ một điểm có tọa độ cho trước đến một đường thẳng có phương trình cho sẵn. Đây là dạng bài tập cơ bản nhất, chỉ cần áp dụng trực tiếp công thức.

Dạng 2: Tìm điểm trên đường thẳng có khoảng cách đến một điểm cho trước bằng một giá trị cho trước. Dạng này thường kết hợp với phương trình đường tròn.

Dạng 3: Chứng minh các điểm có khoảng cách bằng nhau đến một đường thẳng nằm trên một đường thẳng song song với đường thẳng đã cho.

Phương pháp giải và các lưu ý quan trọng

Bước 1: Xác định rõ dạng bài toán và các yếu tố đã cho. Kiểm tra kỹ phương trình đường thẳng, đưa về dạng tổng quát nếu cần.

Bước 2: Chuyển đổi tọa độ điểm và hệ số phương trình về dạng phù hợp với công thức. Đặc biệt lưu ý việc đổi dấu khi chuyển vế.

Bước 3: Áp dụng công thức tính khoảng cách một cách chính xác, không bỏ sót các hệ số. Kiểm tra kết quả bằng cách thế ngược lại.

Bài tập mẫu có lời giải chi tiết

Cho điểm M(2,3) và đường thẳng d: 2x – y + 1 = 0. Tính khoảng cách từ 1 điểm đến 1 đường thẳng d.

Giải:

• Đường thẳng d có dạng ax + by + c = 0 với a = 2, b = -1, c = 1
• Tọa độ điểm M: x0 = 2, y0 = 3
• Áp dụng công thức: d = |2(2) + (-1)(3) + 1|/√(2² + (-1)²)
• Thay số: d = |4 – 3 + 1|/√5 = 2/√5 ≈ 0.89 (đơn vị)

Kết quả được kiểm chứng bằng cách vẽ đường vuông góc từ M đến d.

So sánh công thức tính khoảng cách từ điểm đến đường thẳng và mặt phẳng

Công thức tính khoảng cách từ một điểm đến đường thẳng và công thức tính khoảng cách từ điểm đến mặt phẳng có những điểm tương đồng và khác biệt trong cách biểu diễn toán học. Với đường thẳng, khoảng cách được tính bằng độ dài đường vuông góc từ điểm đến đường thẳng. Còn với mặt phẳng, khoảng cách là độ dài đường vuông góc từ điểm đến mặt phẳng.

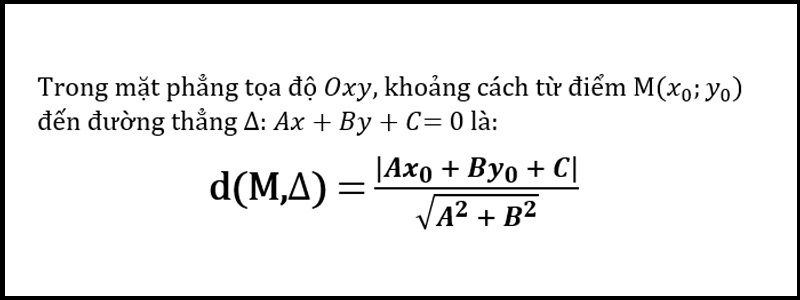
Để tìm hiểu chi tiết về cách tính khoảng cách từ điểm đến mặt phẳng, bạn có thể tham khảo thêm tại khoảng cách từ 1 điểm đến 1 mặt phẳng. Các công thức này đều dựa trên nguyên lý hình học không gian và vector, giúp giải quyết nhiều bài toán thực tế.

Điểm giống và khác nhau giữa hai công thức

Về điểm giống nhau, cả hai công thức đều sử dụng vector pháp tuyến và tọa độ điểm để tính toán. Chúng cũng đều áp dụng nguyên lý chiếu vuông góc và tỷ số độ dài vector để tìm khoảng cách ngắn nhất.

Về khác biệt, công thức tính khoảng cách đến đường thẳng cần vector chỉ phương và một điểm thuộc đường thẳng. Trong khi đó, công thức tính khoảng cách đến mặt phẳng sử dụng vector pháp tuyến và phương trình mặt phẳng. Điều này tạo nên sự khác biệt trong cách biểu diễn và áp dụng.

Tìm hiểu thêm các kiến thức toán học hữu ích tại Hocthenao.vn.

Các trường hợp đặc biệt cần lưu ý

Khi điểm nằm trên đường thẳng hoặc mặt phẳng, khoảng cách sẽ bằng 0. Đây là trường hợp đặc biệt thường gặp trong các bài toán thực tế.

Với đường thẳng song song với trục tọa độ, công thức có thể được đơn giản hóa chỉ còn phụ thuộc vào một tọa độ. Tương tự, với mặt phẳng vuông góc với trục tọa độ, khoảng cách chỉ phụ thuộc vào hiệu của tọa độ tương ứng.

Khi vector chỉ phương của đường thẳng hoặc vector pháp tuyến của mặt phẳng là vector đơn vị, các công thức sẽ trở nên đơn giản hơn, giúp tính toán nhanh chóng và chính xác hơn.

Trong toán học, công thức tính khoảng cách giữa các điểm và các hình học là một phần kiến thức cơ bản nhưng quan trọng. Các công thức này không chỉ giúp học sinh làm tốt các bài tập mà còn dễ dàng ứng dụng vào các vấn đề trong thực tiễn. Việc hiểu rõ các công thức và phương pháp tính khoảng cách sẽ nâng cao kỹ năng giải toán và tạo nền tảng vững chắc cho những kiến thức cao hơn.