Công thức tính tâm I và bán kính R của đường tròn trong hình học phẳng

Công thức tính tâm I và bán kính R của đường tròn là một trong những kiến thức cơ bản trong hình học phẳng. Bài viết này sẽ hướng dẫn bạn phương pháp xác định tọa độ tâm và độ dài bán kính từ phương trình đường tròn. Bên cạnh đó, các ứng dụng trong bài toán thực tế cũng sẽ được trình bày rõ ràng để bạn có thể áp dụng hiệu quả.

Công thức tính tâm I và bán kính R của đường tròn trong hình học phẳng

Công thức tính tâm I và bán kính R của đường tròn là một trong những kiến thức quan trọng trong hình học phẳng. Để xác định tâm I của đường tròn, cần dựa vào các yếu tố đặc trưng như phương trình đường tròn hoặc các điểm đã biết trên đường tròn.

Với phương trình tổng quát của đường tròn (x² + y² + 2ax + 2by + c = 0), tọa độ tâm I được xác định bằng công thức I(-a, -b). Bán kính R của đường tròn sẽ được tính thông qua công thức R = √(a² + b² – c). Việc áp dụng các công thức này giúp giải quyết nhiều bài toán về đường tròn một cách hiệu quả.

Trong trường hợp đường tròn được xác định bởi 3 điểm không thẳng hàng, tâm I chính là giao điểm của hai đường trung trực của hai dây bất kỳ. Bán kính R sẽ là khoảng cách từ tâm I đến một điểm bất kỳ trên đường tròn. Phương pháp này thường được áp dụng khi không có sẵn phương trình đường tròn.

Phương pháp xác định tọa độ tâm I và độ dài bán kính R từ phương trình đường tròn

Việc xác định tọa độ tâm I và bán kính R của đường tròn là một kỹ năng quan trọng trong công thức hình học phẳng. Phương pháp này giúp ta nắm được các thông số cơ bản của đường tròn để giải quyết nhiều bài toán hình học phức tạp hơn.

Khi có phương trình đường tròn dạng (x – a)² + (y – b)² = R², ta có thể xác định ngay tâm I(a,b) và bán kính R. Tuy nhiên với phương trình dạng tổng quát x² + y² + Dx + Ey + F = 0, việc tìm công thức tính tâm I và bán kính R cần thực hiện qua các bước biến đổi đưa về dạng chính tắc.

Từ phương trình tổng quát, ta hoàn chỉnh bình phương để đưa về dạng (x + D/2)² + (y + E/2)² = R², trong đó:

• Tọa độ tâm I(-D/2, -E/2)
• Bán kính R = √((D²+E²)/4 – F)

Phương pháp này áp dụng hiệu quả cho mọi phương trình đường tròn, giúp ta nhanh chóng xác định được vị trí tâm và độ dài bán kính mà không cần thực hiện nhiều phép tính phức tạp. Điều quan trọng là cần nắm vững cách biến đổi để đưa phương trình về dạng chuẩn.

Các trường hợp đặc biệt khi tìm tâm và bán kính đường tròn

Việc tìm tâm và bán kính đường tròn đòi hỏi sự phân tích kỹ lưỡng các điều kiện đặc biệt. Mỗi trường hợp có những đặc điểm riêng biệt cần lưu ý để giải quyết bài toán một cách hiệu quả. Trang web về toán cung cấp nhiều phương pháp giải chi tiết cho từng trường hợp.

Khi xác định tâm và bán kính đường tròn, việc phân loại các trường hợp đặc biệt giúp đơn giản hóa quá trình giải và tránh nhầm lẫn. Ba trường hợp phổ biến nhất là đường tròn tiếp xúc với trục tọa độ, đường tròn đi qua gốc tọa độ và đường tròn cắt trục tọa độ.

Đường tròn tiếp xúc với trục tọa độ

Khi đường tròn tiếp xúc với một hoặc cả hai trục tọa độ, tọa độ tâm và bán kính có mối liên hệ đặc biệt. Nếu đường tròn tiếp xúc với trục hoành, hoành độ của điểm tiếp xúc chính là hoành độ của một điểm đã biết trên đường tròn.

Trong trường hợp tiếp xúc với trục tung, tung độ của điểm tiếp xúc bằng tung độ của điểm đã cho. Khoảng cách từ tâm đến trục tiếp xúc luôn bằng bán kính đường tròn.

Đường tròn đi qua gốc tọa độ

Đường tròn đi qua gốc tọa độ có phương trình đặc trưng không chứa số hạng tự do. Tọa độ tâm và bán kính có thể xác định thông qua việc biến đổi phương trình về dạng chính tắc.

Khi biết thêm một điểm khác ngoài gốc tọa độ, ta có thể dựng được đường trung trực của đoạn thẳng nối hai điểm. Giao điểm của đường trung trực với đường vuông góc tại gốc tọa độ chính là tâm đường tròn.

Đường tròn cắt trục tọa độ

Đường tròn cắt trục tọa độ tạo ra các giao điểm có tọa độ đặc biệt. Nếu cắt trục hoành, tung độ của giao điểm bằng 0. Nếu cắt trục tung, hoành độ của giao điểm bằng 0.

Từ các giao điểm với trục tọa độ, kết hợp với điều kiện về khoảng cách từ tâm đến các điểm trên đường tròn bằng nhau, ta thiết lập được hệ phương trình để tìm tọa độ tâm. Bán kính được xác định bằng khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn.

Ứng dụng công thức tính tâm I và bán kính R trong giải toán hình học

Việc áp dụng công thức tính tâm i và bán kính r đóng vai trò quan trọng trong việc giải các bài toán hình học. Công thức này giúp xác định chính xác vị trí tâm và độ dài bán kính của đường tròn, từ đó làm cơ sở để giải quyết nhiều dạng toán phức tạp.

Khi giải toán về hình tròn, việc nắm vững các công thức hình tròn sẽ giúp học sinh tiếp cận bài toán một cách có hệ thống. Đặc biệt trong các bài toán về tiếp tuyến và góc, việc xác định tâm và bán kính là bước đầu tiên không thể thiếu.

Các phép tính toán hình tròn thường đòi hỏi sự kết hợp giữa nhiều kiến thức như tam giác đồng dạng, định lý Pythagoras và công thức thể tích khối tròn xoay. Việc vận dụng linh hoạt các công thức sẽ giúp giải quyết bài toán hiệu quả.

Bài toán về diện tích hình tròn

Trong các bài toán về diện tích hình tròn, việc xác định tâm và bán kính là yếu tố then chốt. Khi đã có được tọa độ tâm I, ta có thể tính được khoảng cách từ tâm đến các điểm trên đường tròn, từ đó xác định bán kính R.

Nhiều bài toán yêu cầu tính diện tích phần giao nhau giữa hai hình tròn hoặc giữa hình tròn với các hình khác. Trong trường hợp này, việc xác định chính xác vị trí tâm và độ dài bán kính sẽ giúp áp dụng đúng công thức tính diện tích phần giao.

Bài toán về chu vi hình tròn

Khi giải các bài toán liên quan đến chu vi hình tròn, việc tìm bán kính R thông qua tọa độ tâm I là bước quan trọng. Từ đó, ta có thể tính được độ dài cung tròn hoặc chu vi của các hình có chứa cung tròn.

Trong thực tế, nhiều công trình kiến trúc và thiết kế đều áp dụng các tính toán về chu vi hình tròn. Ví dụ như việc tính toán lượng vật liệu cần thiết để làm lan can cong cho ban công tròn hay tính độ dài đường viền trang trí hình tròn.

Bài toán về tiếp tuyến

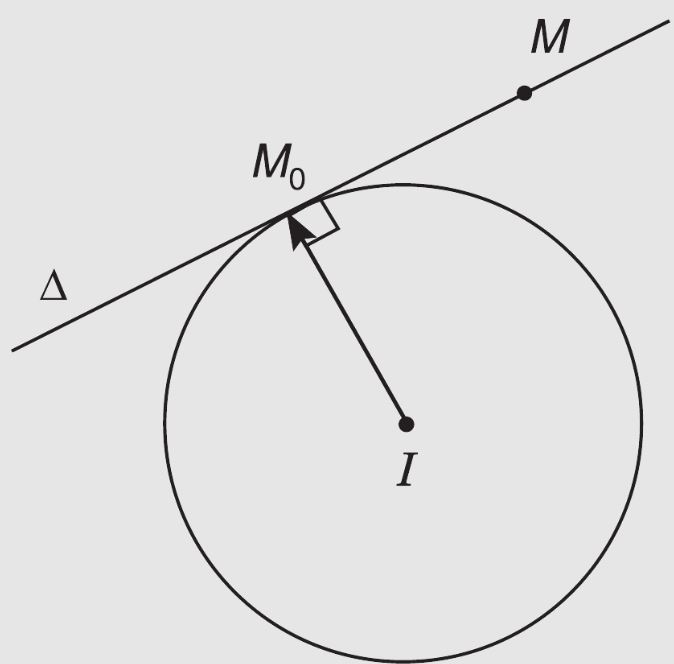
Các bài toán về tiếp tuyến thường yêu cầu xác định điểm tiếp xúc giữa đường thẳng và đường tròn. Để giải được dạng toán này, việc nắm vững tính chất vuông góc giữa bán kính và tiếp tuyến tại điểm tiếp xúc là rất quan trọng.

Trong các ứng dụng thực tế, tiếp tuyến của đường tròn được sử dụng nhiều trong thiết kế đường cong cho các công trình giao thông. Các kỹ sư phải tính toán chính xác góc giữa tiếp tuyến và bán kính để đảm bảo độ an toàn cho các phương tiện khi di chuyển.

Việc xác định tiếp tuyến chung của hai đường tròn cũng là một dạng toán phổ biến, đòi hỏi phải nắm vững các tính chất về khoảng cách từ tâm đến tiếp tuyến và quan hệ giữa các bán kính

Mở rộng kiến thức về tâm và bán kính trong không gian ba chiều

Trong không gian ba chiều, việc xác định tâm và bán kính của các hình khối có vai trò quan trọng trong tính toán diện tích, thể tích cũng như các đặc trưng hình học khác. Công thức tính tâm i và bán kính r của mỗi hình khối có những đặc điểm riêng biệt, phụ thuộc vào cấu trúc hình học của chúng.

Tâm và bán kính mặt cầu

Mặt cầu là tập hợp các điểm trong không gian cách đều một điểm cố định gọi là tâm. Công thức tính tâm của mặt cầu được xác định bởi tọa độ (x0, y0, z0) của điểm tâm trong hệ tọa độ Descartes. Công thức tính bán kính mặt cầu giúp xác định khoảng cách từ tâm đến mọi điểm trên mặt cầu.

Trong thực tế, việc xác định tâm và bán kính mặt cầu được ứng dụng rộng rãi trong thiết kế kiến trúc. Ví dụ như mái vòm của nhà thờ St. Peter’s Basilica tại Vatican được thiết kế dựa trên nguyên lý hình học của mặt cầu với tâm và bán kính được tính toán chính xác.

Tâm và bán kính hình nón

Hình nón có tâm là điểm nằm trên trục đối xứng và cách đều đỉnh nón với mặt phẳng đáy. Bán kính hình tròn đáy của nón được xác định bằng khoảng cách từ tâm đáy đến điểm bất kỳ trên đường tròn đáy.

Trong công nghiệp, việc tính toán tâm và bán kính hình nón đóng vai trò quan trọng trong sản xuất các chi tiết máy như ống phễu, phụ tùng ô tô. Các kỹ sư thường sử dụng phần mềm CAD để mô phỏng và tối ưu hóa các thông số này.

Tâm và bán kính hình trụ

Hình trụ có tâm nằm trên trục đối xứng, là điểm cách đều hai mặt phẳng đáy. Việc xác định tâm và bán kính hình trụ cần dựa vào hai yếu tố: tọa độ tâm của hai mặt đáy và khoảng cách từ tâm đến điểm bất kỳ trên đường tròn đáy.

Trong xây dựng, cột trụ tròn thường được thiết kế dựa trên các tính toán về tâm và bán kính. Theo tiêu chuẩn xây dựng TCVN, độ lệch tâm cho phép của cột trụ tròn không được vượt quá 1/500 chiều cao cột để đảm bảo tính ổn định của công trình.

Các công trình hiện đại như tháp truyền hình CN Tower tại Toronto, Canada sử dụng hệ thống cột trụ với tâm và bán kính được tính toán chính xác để chống chịu tải trọng gió và động đất hiệu quả.

Phương pháp kiểm tra và rèn luyện kỹ năng tính tâm I và bán kính R

Để nắm vững công thức tính tâm i và bán kính r, học sinh cần thực hành giải nhiều dạng bài tập khác nhau. Việc rèn luyện thường xuyên giúp phát triển tư duy hình học và khả năng phân tích hình vẽ chính xác.

Khi áp dụng cách tính tâm i, điều quan trọng là xác định đúng các yếu tố hình học liên quan như đường cao, đường trung tuyến và đường phân giác. Mỗi yếu tố này đều có vai trò riêng trong việc xác định vị trí tâm đường tròn nội tiếp.

Ngoài ra, cách tìm tâm i còn đòi hỏi sự thành thạo trong việc sử dụng các công thức tính diện tích tam giác và các định lý về đường tròn nội tiếp. Việc nắm vững các kiến thức nền tảng này sẽ giúp giải quyết bài toán nhanh chóng và chính xác hơn.

Bài tập mẫu có lời giải

Bài toán: Cho tam giác ABC có các cạnh a = 13cm, b = 14cm, c = 15cm. Tính bán kính đường tròn nội tiếp của tam giác.

Lời giải:

• Bước 1: Tính nửa chu vi p = (a + b + c)/2 = 21cm
• Bước 2: Tính diện tích tam giác S = √(p(p-a)(p-b)(p-c)) = 84cm²
• Bước 3: Áp dụng công thức r = S/p = 4cm

Kết quả cho thấy bán kính đường tròn nội tiếp của tam giác là 4cm.

Các dạng bài tập thường gặp

Trong chương trình hình học, các bài toán về tâm và bán kính đường tròn nội tiếp thường xuất hiện dưới nhiều hình thức đa dạng. Một số dạng phổ biến bao gồm tìm tâm đường tròn nội tiếp khi biết các yếu tố của tam giác như cạnh, góc hoặc diện tích.

Các bài toán nâng cao thường yêu cầu chứng minh mối quan hệ giữa tâm đường tròn nội tiếp với các yếu tố khác của tam giác. Việc giải quyết những bài toán này đòi hỏi kiến thức tổng hợp và kỹ năng phân tích sâu sắc.

Mẹo giải nhanh

Khi giải các bài toán về tâm và bán kính đường tròn nội tiếp, việc nhận diện nhanh các yếu tố đã cho và mối liên hệ giữa chúng là rất quan trọng. Một số mẹo hữu ích là vẽ phác thảo hình để hình dung rõ ràng các yếu tố cần tìm.

Trong trường hợp bài toán phức tạp, có thể chia nhỏ thành các bước giải quyết đơn giản hơn. Việc áp dụng các công thức tính nhanh như r = S/p hoặc sử dụng tính chất của đường phân giác sẽ giúp rút ngắn thời gian giải bài.

Nắm vững các công thức cơ bản và thực hành nhiều bài tập đa dạng sẽ giúp phát triển khả năng giải nhanh các bài toán về đường tròn nội tiếp một cách hiệu quả.

Trong hình học phẳng, công thức tính tâm I và bán kính R là chìa khóa giúp bạn xác định đặc điểm của đường tròn. Bài viết đã tổng hợp phương pháp xác định tọa độ tâm và độ dài bán kính từ phương trình đường tròn, cũng như cách xử lý các trường hợp đặc biệt. Việc nắm vững kiến thức này sẽ hỗ trợ bạn rất nhiều trong việc giải bài tập hình học một cách hiệu quả và chính xác.