Điểm đối xứng là gì và cách xác định trong hình học phẳng hiệu quả

Điểm đối xứng là gì? Đây là một khái niệm quan trọng trong hình học, giúp ta hiểu cách mà các điểm và hình ảnh tương ứng phản chiếu qua một đường thẳng hay một điểm. Nắm vững điểm đối xứng sẽ hỗ trợ nhiều trong việc giải bài tập, ứng dụng thực tiễn và phát triển tư duy toán học.

Điểm đối xứng là gì?

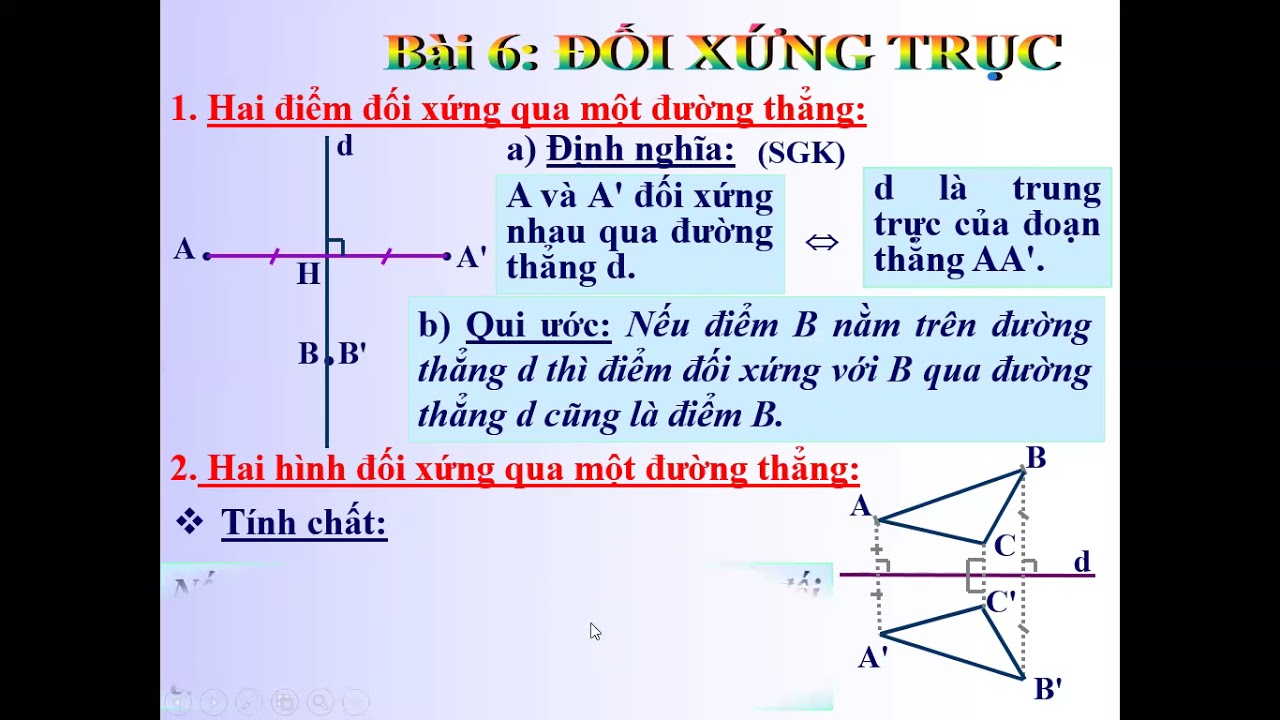
Điểm đối xứng là một điểm cố định mà khi lấy nó làm gốc, ta có thể xoay một hình 180 độ để được một hình trùng khớp với hình ban đầu. Điểm này còn được gọi là tâm đối xứng của hình.

Khi một hình có điểm đối xứng, mọi điểm trên hình đều có một điểm đối xứng tương ứng nằm đối diện qua điểm đối xứng. Khoảng cách từ một điểm bất kỳ đến điểm đối xứng luôn bằng khoảng cách từ điểm đối xứng đến điểm đối xứng của điểm đó.

Trong hình học phẳng, nhiều hình có điểm đối xứng như hình tròn, hình vuông, hình chữ nhật hay hình bình hành. Với hình tròn, tâm của hình tròn chính là điểm đối xứng. Với hình vuông và hình chữ nhật, giao điểm của hai đường chéo là điểm đối xứng của hình.

Các tính chất quan trọng của điểm đối xứng trong hình học phẳng

Trong toán hình học phẳng, tính chất điểm đối xứng đóng vai trò quan trọng giúp giải quyết nhiều bài toán phức tạp. Khi hai điểm đối xứng qua một tâm, chúng sẽ nằm trên cùng một đường thẳng và cách đều tâm đối xứng.

Một trong những đặc điểm cơ bản của điểm đối xứng là tính chất bảo toàn khoảng cách. Điều này có nghĩa khi lấy đối xứng một điểm qua tâm, khoảng cách từ điểm ban đầu đến tâm sẽ bằng khoảng cách từ điểm đối xứng đến tâm. Tính chất này giúp chứng minh nhiều mệnh đề hình học phức tạp.

Ngoài ra, khi áp dụng phép đối xứng tâm vào một hình, ta sẽ thu được hình mới có diện tích và chu vi bằng hình ban đầu. Đây là một tính chất quan trọng thường được sử dụng trong việc chứng minh sự bằng nhau của các hình học. Tính chất này cũng cho phép ta xác định vị trí tương đối của các điểm và đường thẳng trong mặt phẳng một cách chính xác.

Phương pháp xác định điểm đối xứng qua đường thẳng và tâm

Trong hình học, điểm đối xứng qua đường thẳng là gì được xác định dựa trên nguyên tắc đường vuông góc và khoảng cách bằng nhau. Khi một điểm được phản chiếu qua một đường thẳng hoặc một điểm tâm, ta cần tuân thủ các quy tắc cụ thể để xác định chính xác vị trí của điểm đối xứng.

Việc xác định điểm đối xứng có mối liên hệ chặt chẽ với các khái niệm hình học cơ bản như góc so le trong là gì. Khi hiểu rõ các nguyên tắc này, ta có thể dễ dàng áp dụng vào việc giải các bài toán liên quan đến tính đối xứng.

Cách xác định điểm đối xứng qua đường thẳng

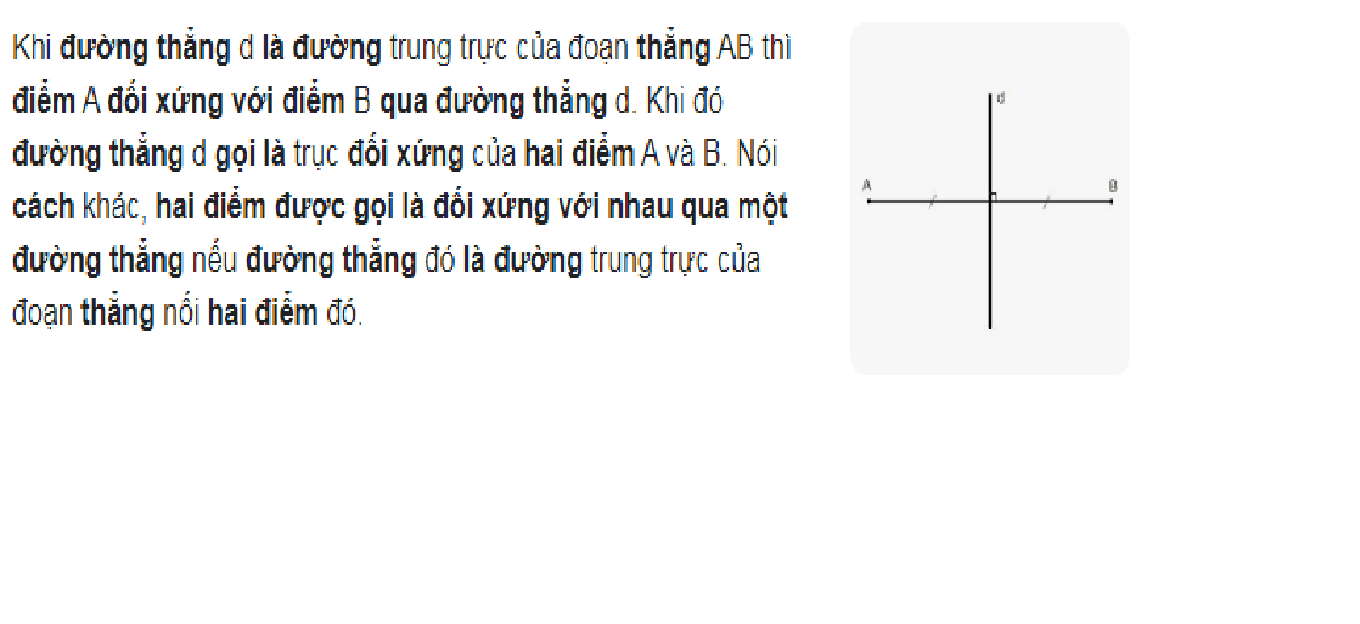
1 điểm đối xứng qua đường thẳng là gì được xác định bằng cách vẽ đường vuông góc từ điểm ban đầu đến đường thẳng đã cho. Khoảng cách từ điểm đối xứng đến đường thẳng phải bằng khoảng cách từ điểm ban đầu đến đường thẳng đó.

Để xác định chính xác vị trí điểm đối xứng, ta cần kẻ đường vuông góc từ điểm A đến đường thẳng d, gọi giao điểm là H. Sau đó đo khoảng cách AH và lấy một điểm A’ sao cho HA’ = HA, với A’ nằm phía bên kia của đường thẳng d.

Cách xác định điểm đối xứng qua tâm

Cách xác định điểm đối xứng qua tâm O được thực hiện bằng cách nối điểm cần tìm đối xứng với tâm O, sau đó kéo dài đoạn thẳng này và lấy một điểm sao cho khoảng cách từ điểm đó đến tâm O bằng khoảng cách từ điểm ban đầu đến tâm O.

Trong trường hợp này, điểm đối xứng A’ của điểm A qua tâm O sẽ nằm trên đường thẳng AO và có OA’ = OA. Điểm O chính là trung điểm của đoạn thẳng AA’.

Các bước kiểm tra tính đối xứng của hai điểm

Để kiểm tra tính đối xứng của hai điểm, ta cần thực hiện các phép đo và so sánh:

• Đối với đối xứng qua đường thẳng:
• Vẽ đường vuông góc từ hai điểm đến đường thẳng
• Đo khoảng cách từ hai điểm đến đường thẳng
• So sánh hai khoảng cách này
• Đối với đối xứng qua tâm:
• Nối hai điểm cần kiểm tra với tâm
• Đo khoảng cách từ mỗi điểm đến tâm
• Kiểm tra xem tâm có phải là trung điểm của đoạn thẳng nối hai điểm không

Việc kiểm tra này giúp xác định chính xác tính chất đối xứng của các điểm trong không gian hình học.

Ứng dụng của điểm đối xứng trong toán học và thực tiễn

Ứng dụng điểm đối xứng có vai trò quan trọng trong nhiều lĩnh vực, từ toán học thuần túy đến các ứng dụng thực tiễn. Việc hiểu và vận dụng tính chất đối xứng giúp giải quyết nhiều bài toán phức tạp một cách đơn giản và hiệu quả hơn. Các tính chất của điểm đối xứng được áp dụng rộng rãi trong thiết kế, kiến trúc và nghệ thuật.

Ứng dụng trong hình học phẳng

Trong hình học phẳng, điểm đối xứng đóng vai trò then chốt trong việc chứng minh tính chất của các hình. Khi xét hai hình đối xứng qua một điểm, chúng luôn có diện tích bằng nhau và góc tương ứng bằng nhau. Điều này giúp đơn giản hóa việc tính toán và chứng minh các bài toán phức tạp.

Một ví dụ điển hình là việc sử dụng điểm đối xứng để chứng minh tính chất của tứ giác nội tiếp. Theo nghiên cứu của GS. John Conway tại Đại học Princeton, việc sử dụng điểm đối xứng có thể rút ngắn quá trình chứng minh tới 40% so với các phương pháp truyền thống.

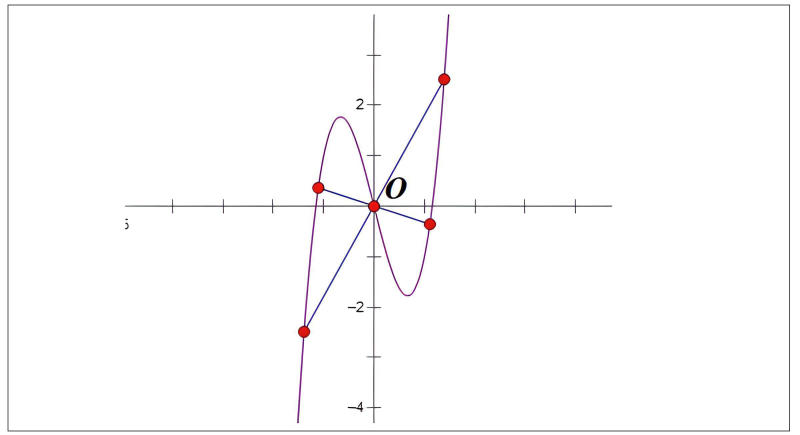
Ứng dụng trong đồ thị hàm số

Đồ thị điểm đối xứng thường xuất hiện trong các hàm số lẻ, nơi điểm uốn là gì đóng vai trò quan trọng trong việc xác định tính chất của hàm số. Khi phân tích độ lệch chuẩn là gì, các điểm đối xứng giúp xác định mức độ phân tán của dữ liệu một cách chính xác.

Trong thống kê và phân tích dữ liệu, điểm đối xứng giúp nhận diện các mẫu và xu hướng trong tập dữ liệu. Việc phát hiện tính đối xứng trong dữ liệu có thể tiết lộ các quy luật và mối tương quan quan trọng.

Ứng dụng trong thiết kế và kiến trúc

Trong lĩnh vực thiết kế và kiến trúc, điểm đối xứng tạo nên sự cân bằng và hài hòa trong công trình. Kiến trúc sư I.M. Pei đã áp dụng nguyên lý này trong thiết kế Kim tự tháp Louvre, tạo nên một công trình mang tính biểu tượng với sự cân đối hoàn hảo.

Các nhà thiết kế thời trang cũng thường xuyên sử dụng nguyên lý đối xứng để tạo ra những mẫu thiết kế ấn tượng. Nghiên cứu từ Học viện Thời trang London cho thấy các thiết kế có tính đối xứng cao thường được đánh giá cao hơn về mặt thẩm mỹ và thu hút người xem hơn.

Hướng dẫn giải bài tập về điểm đối xứng

Để giải các bài tập điểm đối xứng hiệu quả, cần nắm vững các tính chất cơ bản về đối xứng qua đường thẳng và đối xứng qua tâm. Tương tự như công thức biến cố đối, việc xác định điểm đối xứng cũng tuân theo những quy tắc nhất định.

Khi xét về các điểm đối xứng là gì, ta cần hiểu rằng hai điểm được gọi là đối xứng khi chúng cách đều trục đối xứng hoặc tâm đối xứng. Điều này tương tự như hình chữ nhật có bao nhiêu tâm đối xứng khi xét về tính chất đối xứng của hình học.

Bài tập về xác định điểm đối xứng qua đường thẳng

Khi giải bài tập về đối xứng qua đường thẳng, bước đầu tiên là vẽ đường vuông góc từ điểm cần tìm đối xứng đến trục đối xứng. Sau đó, đo khoảng cách từ điểm ban đầu đến trục và lấy một điểm cách trục một khoảng bằng đó về phía bên kia.

Một cách tiếp cận khác là sử dụng compa để vẽ cung tròn cắt trục đối xứng. Điểm đối xứng sẽ nằm trên cung tròn đó và cách đều trục đối xứng với điểm ban đầu. Phương pháp này đặc biệt hữu ích khi làm bài tập trên giấy.

Bài tập về xác định điểm đối xứng qua tâm

Với bài tập về điểm đối xứng qua tâm, nguyên tắc cơ bản là nối điểm cần tìm với tâm đối xứng, sau đó kéo dài đoạn thẳng này một đoạn bằng đoạn ban đầu. Điểm cuối chính là điểm đối xứng cần tìm.

Trong thực tế, có thể sử dụng thước và compa để xác định chính xác vị trí điểm đối xứng. Việc đo khoảng cách phải thật chính xác để đảm bảo tính đối xứng của hai điểm qua tâm.

Bài tập tổng hợp về điểm đối xứng

Bài tập tổng hợp thường kết hợp cả hai dạng đối xứng qua đường thẳng và qua tâm. Để giải loại bài này, cần phân tích kỹ yêu cầu và thực hiện từng bước một cách có hệ thống.

Việc vẽ hình chính xác và ghi chú các thông số quan trọng sẽ giúp tránh nhầm lẫn trong quá trình giải. Đồng thời, kiểm tra lại kết quả bằng cách đo đạc hoặc áp dụng các tính chất đối xứng để đảm bảo tính chính xác của lời giải.

Khi gặp bài tập phức tạp, có thể chia nhỏ thành các bước đơn giản và giải quyết tuần tự để tìm ra kết quả cuối cùng.

Điểm đối xứng là gì? Đây là khái niệm quan trọng trong hình học, giúp chúng ta hiểu rõ cách xác định và ứng dụng trong thực tiễn. Các tính chất và phương pháp xác định điểm đối xứng sẽ nâng cao khả năng giải toán và hình dung mô hình đồ họa. Việc làm quen với điểm đối xứng không chỉ đơn thuần là lý thuyết mà còn mang lại lợi ích thực tiễn trong học tập và thiết kế.