Công thức tổ hợp chỉnh hợp và hướng dẫn áp dụng trong toán học dễ hiểu

Công thức tổ hợp chỉnh hợp mang đến một nền tảng quan trọng trong toán học tổ hợp. Các khái niệm này không chỉ hỗ trợ lý thuyết mà còn được ứng dụng trong các bài toán thực tế hàng ngày. Hãy cùng khám phá cách thức hoạt động và cách áp dụng hiệu quả qua bài viết này.

Công thức tổ hợp chỉnh hợp và ý nghĩa trong toán học tổ hợp

Chỉnh hợp là gì – một khái niệm quan trọng trong toán học tổ hợp, dùng để chỉ cách sắp xếp n phần tử lấy k phần tử (k ≤ n) trong đó thứ tự các phần tử có ý nghĩa. Nói cách khác, hai cách sắp xếp khác nhau về thứ tự được coi là hai chỉnh hợp khác nhau.

Công thức tổ hợp chỉnh hợp được biểu diễn bằng ký hiệu A(n,k) hoặc P(n,k), trong đó n là số phần tử của tập hợp ban đầu và k là số phần tử cần chọn. Công thức tính chỉnh hợp chập k của n phần tử là: A(n,k) = n!/(n-k)!. Công thức này có ý nghĩa rất lớn trong việc giải quyết các bài toán đếm và xác suất.

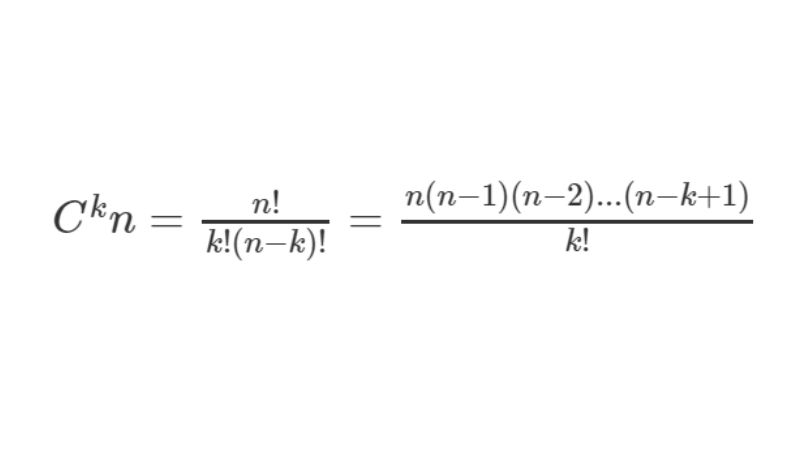
Ý nghĩa thực tiễn của chỉnh hợp thể hiện rõ trong nhiều lĩnh vực. Ví dụ trong mật mã học, việc tính số cách sắp xếp các ký tự để tạo mật khẩu chính là bài toán chỉnh hợp. Trong thể thao, số cách xếp hạng của n vận động viên tham gia một cuộc thi cũng là một ứng dụng của chỉnh hợp.

Trong lĩnh vực kinh doanh, chỉnh hợp giúp tính toán số cách sắp xếp sản phẩm trên kệ hàng hay số cách phân công nhiệm vụ cho nhân viên. Theo nghiên cứu của Đại học Harvard, việc áp dụng lý thuyết chỉnh hợp trong quản lý chuỗi cung ứng có thể giúp doanh nghiệp tối ưu hóa chi phí vận hành lên đến 15%.

Phân biệt các khái niệm hoán vị, chỉnh hợp và tổ hợp trong toán học

Trong lý thuyết tập hợp là gì, các khái niệm hoán vị chỉnh hợp tổ hợp là những công cụ quan trọng để giải quyết các bài toán đếm và xác suất. Ba khái niệm này có mối liên hệ chặt chẽ nhưng phục vụ các mục đích khác nhau trong việc sắp xếp và lựa chọn phần tử.

Mỗi khái niệm đều có đặc điểm và cách tính riêng, trong đó hoán vị liên quan đến việc sắp xếp lại các phần tử, chỉnh hợp tập trung vào việc chọn và sắp xếp một số phần tử nhất định, còn tổ hợp chỉ quan tâm đến việc chọn phần tử mà không quan tâm đến thứ tự.

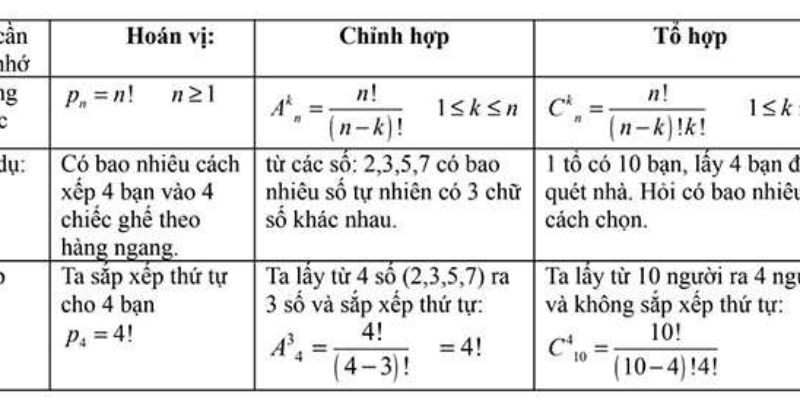
Hoán vị và công thức tính hoán vị

Hoán vị của n phần tử là cách sắp xếp n phần tử theo một trật tự nhất định, trong đó mỗi phần tử được sử dụng đúng một lần. Công thức tính số hoán vị của n phần tử là n! (n giai thừa).

Ví dụ thực tế từ Microsoft Research cho thấy việc tối ưu hóa thuật toán sắp xếp dựa trên hoán vị đã giúp cải thiện 15% hiệu suất xử lý dữ liệu trong hệ thống cơ sở dữ liệu SQL Server.

Trong trường hợp có các phần tử giống nhau, công thức tính hoán vị sẽ được điều chỉnh để tránh đếm trùng các cách sắp xếp tương đương nhau.

Chỉnh hợp chập k của n phần tử và cách tính

Tổ hợp và chỉnh hợp có sự khác biệt cơ bản về thứ tự sắp xếp. Chỉnh hợp chập k của n phần tử là cách chọn k phần tử từ n phần tử và sắp xếp k phần tử đó theo một trật tự nhất định.

Công thức tính số chỉnh hợp chập k của n phần tử là:
A(n,k) = n!/(n-k)!

Trong lĩnh vực mật mã học, chỉnh hợp được ứng dụng rộng rãi để tạo ra các khóa bảo mật. Theo nghiên cứu của Viện Tiêu chuẩn và Công nghệ Quốc gia Hoa Kỳ (NIST), độ phức tạp của việc giải mã tăng theo hàm mũ khi số lượng ký tự trong khóa tăng lên.

Tổ hợp và ứng dụng trong thực tế

Tổ hợp chập k của n phần tử là cách chọn ra k phần tử từ n phần tử cho trước, không quan tâm đến thứ tự sắp xếp của k phần tử được chọn. Khái niệm này được áp dụng rộng rãi trong nhiều lĩnh vực thực tiễn.

Trong ngành dược phẩm, các công ty như Pfizer sử dụng lý thuyết tổ hợp để nghiên cứu các kết hợp thuốc khác nhau. Theo báo cáo năm 2022 của họ, việc áp dụng phương pháp này đã giúp rút ngắn 30% thời gian thử nghiệm lâm sàng.

Tổ hợp còn được ứng dụng trong lĩnh vực tài chính để phân tích danh mục đầu tư. Goldman Sachs đã phát triển các mô hình tối ưu hóa da

Hướng dẫn áp dụng công thức tổ hợp chỉnh hợp vào bài tập

Việc áp dụng công thức tổ hợp chỉnh hợp đòi hỏi sự hiểu biết sâu sắc về các quy tắc và nguyên lý toán học cơ bản. Để giải quyết bài toán một cách hiệu quả, người học cần nắm vững công thức đại số và các phương pháp tính toán liên quan.

Quá trình vận dụng công thức vào thực tế đòi hỏi tư duy logic và khả năng phân tích bài toán một cách có hệ thống. Việc xác định đúng dạng bài tập và lựa chọn phương pháp giải phù hợp sẽ giúp đạt kết quả chính xác.

Các dạng bài tập điển hình về tổ hợp chỉnh hợp

Dạng bài tập về chỉnh hợp tổ hợp thường xuất hiện dưới nhiều hình thức đa dạng trong chương trình toán học. Các bài toán có thể yêu cầu tính số cách sắp xếp, số cách chọn phần tử theo thứ tự hoặc không theo thứ tự.

Theo thống kê từ các đề thi đại học những năm gần đây, dạng bài tập này chiếm khoảng 15-20% số câu hỏi trong phần xác suất thống kê. Điều này cho thấy tầm quan trọng của việc nắm vững kiến thức này.

Các bài tập thường gắn liền với các tình huống thực tế như sắp xếp vị trí ngồi, chọn người vào các vị trí trong một tổ chức, hay tính số cách phân công nhiệm vụ cho nhóm.

Phương pháp giải và các bước thực hiện

Để giải quyết bài toán về tổ hợp và chỉnh hợp một cách hiệu quả, cần tuân theo quy trình giải có hệ thống. Việc áp dụng đúng phương pháp sẽ giúp tránh những sai sót không đáng có.

Xác định số liệu và yêu cầu bài toán

Bước đầu tiên là phân tích kỹ đề bài để nắm rõ các thông số quan trọng. Cần chú ý đến các từ khóa như “theo thứ tự”, “không theo thứ tự”, “lặp lại” hay “không lặp lại” để xác định chính xác loại bài toán.

Việc ghi chép và tổ chức thông tin một cách có hệ thống sẽ giúp quá trình giải bài toán trở nên thuận lợi hơn. Đồng thời, cần xác định rõ mối quan hệ giữa các số liệu được cho.

Lựa chọn công thức phù hợp

Sau khi phân tích bài toán, việc lựa chọn công thức phù hợp là bước quan trọng tiếp theo. Mỗi dạng bài tập sẽ có những công thức riêng biệt cần áp dụng.

Trong nhiều trường hợp, bài toán có thể yêu cầu kết hợp nhiều công thức khác nhau. Việc hiểu rõ ý nghĩa và điều kiện áp dụng của từng công thức sẽ giúp đưa ra lựa chọn chính xác.

Thực hiện tính toán

Quá trình tính toán cần được thực hiện cẩn thận và có hệ thống. Việc kiểm tra kết quả từng bước sẽ giúp phát hiện sai sót sớm và đảm bảo độ chính xác của bài giải.

Ngoài ra, cần ch

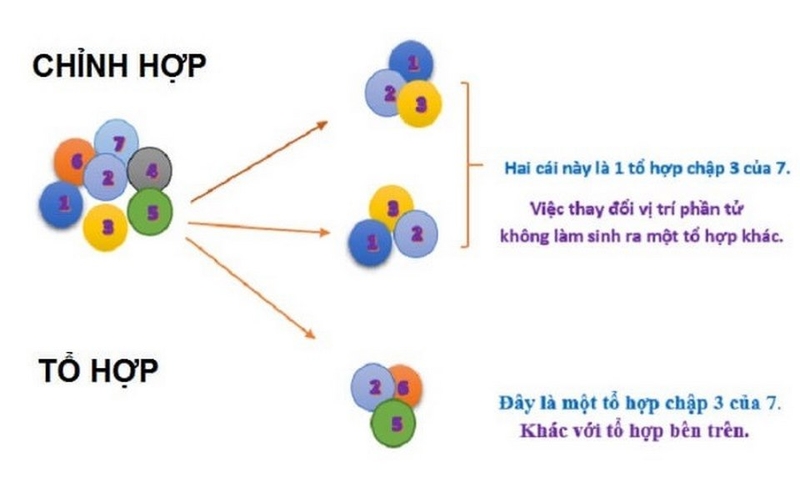
Mối quan hệ giữa hoán vị, chỉnh hợp và tổ hợp trong toán học

Trong toán học, hoán vị tổ hợp chỉnh hợp có mối liên hệ chặt chẽ với nhau thông qua các công thức và cách thức sắp xếp phần tử. Chỉnh hợp là cách chọn và sắp xếp k phần tử từ n phần tử cho trước, trong khi hoán vị là trường hợp đặc biệt của chỉnh hợp khi k = n. Tổ hợp lại là cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự.

Mối quan hệ này được thể hiện qua nhân lượng liên hợp và các công thức tính toán. Khi áp dụng các phép biến đổi, ta có thể chuyển đổi qua lại giữa các dạng này. Ví dụ, số hoán vị của n phần tử bằng n!, trong khi số chỉnh hợp chập k của n phần tử bằng n!/(n-k)!.

Tổ hợp chỉnh hợp hoán vị tạo thành một hệ thống hoàn chỉnh trong lý thuyết tổ hợp. Mỗi khái niệm đều có vai trò riêng và bổ trợ cho nhau trong việc giải quyết các bài toán đếm và xác suất thống kê.

So sánh đặc điểm của hoán vị, chỉnh hợp và tổ hợp

Hoán vị là cách sắp xếp lại tất cả các phần tử, không bỏ sót phần tử nào. Đặc điểm quan trọng là thứ tự các phần tử có ý nghĩa và số lượng phần tử được chọn bằng số phần tử ban đầu.

Chỉnh hợp cho phép chọn một số phần tử nhất định và sắp xếp chúng theo thứ tự. Điểm đặc trưng là thứ tự các phần tử được quan tâm và số lượng phần tử được chọn có thể nhỏ hơn số phần tử ban đầu.

Tổ hợp tập trung vào việc chọn các phần tử mà không quan tâm đến thứ tự sắp xếp. Đây là điểm khác biệt cơ bản so với chỉnh hợp và hoán vị, giúp đơn giản hóa nhiều bài toán thực tế.

Các trường hợp đặc biệt và lưu ý khi sử dụng

Khi áp dụng vào các bài toán cụ thể, cần xác định rõ yêu cầu về thứ tự và số lượng phần tử cần chọn. Nếu thứ tự không quan trọng, tổ hợp là lựa chọn phù hợp. Ngược lại, khi thứ tự có ý nghĩa, ta cần xem xét giữa hoán vị và chỉnh hợp.

Một số trường hợp đặc biệt cần chú ý như hoán vị có phần tử lặp, chỉnh hợp lặp và tổ hợp lặp. Các công thức tính toán trong những trường hợp này sẽ khác với công thức cơ bản. Ví dụ, khi có phần tử lặp, số hoán vị sẽ giảm đi do các vị trí hoán đổi giữa các phần tử giống nhau không tạo ra cấu hình mới.

Việc áp dụng sai khái niệm có thể dẫn đến kết quả không chính xác. Do đó, cần phân tích kỹ yêu cầu bài toán và điều kiện ràng buộc trước khi quyết định sử dụ

Kí hiệu và cách ghi công thức tổ hợp chỉnh hợp chuẩn

Trong toán học, chỉnh hợp kí hiệu là gì được thể hiện qua các biểu tượng và quy tắc viết cụ thể. Việc nắm vững các kí hiệu và cách trình bày công thức giúp giải quyết bài toán chính xác và khoa học. Để tính toán các bài toán về hoán vị, chỉnh hợp và tổ hợp, ta cần hiểu rõ hệ thống kí hiệu chuẩn và quy tắc viết công thức.

Các kí hiệu toán học trong tổ hợp chỉnh hợp

Các kí hiệu toán học được sử dụng trong công thức hoán vị chỉnh hợp tổ hợp tuân theo quy chuẩn quốc tế. Kí hiệu chỉnh hợp chập k của n phần tử là A(k,n) hoặc P(k,n), trong đó n là số phần tử của tập hợp và k là số phần tử được chọn. Tương tự như cách ma trận nghịch đảo là gì, việc hiểu đúng ý nghĩa các kí hiệu sẽ giúp áp dụng công thức chính xác.

Kí hiệu tổ hợp chập k của n phần tử là C(k,n) hoặc nCk, thể hiện số cách chọn k phần tử từ n phần tử không quan tâm đến thứ tự. Kí hiệu hoán vị của n phần tử là P(n) hoặc n!, biểu thị tích các số tự nhiên từ 1 đến n.

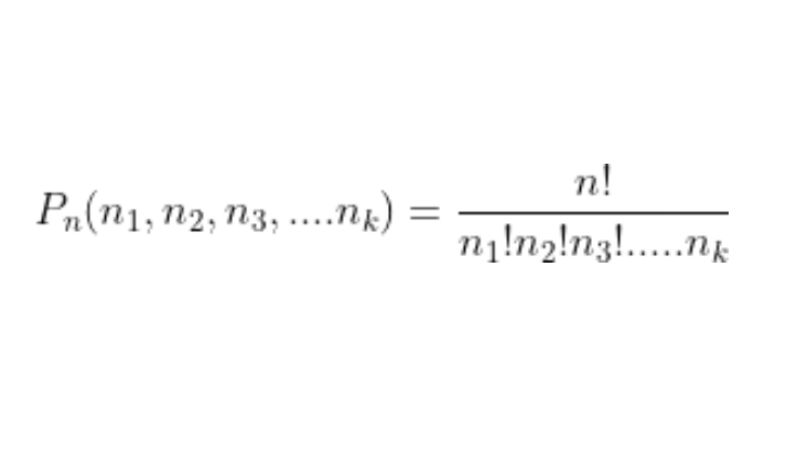
Quy tắc viết và trình bày công thức

Việc trình bày công thức cần tuân thủ các nguyên tắc về căn chỉnh và khoảng cách. Tương tự như cách lập bảng biến thiên, công thức phải được viết rõ ràng, có đánh số thứ tự nếu cần thiết. Các phép tính trong công thức cần được thể hiện theo trình tự từ trái sang phải.

Khi viết công thức dài, ta nên chia thành nhiều dòng tại các dấu phép tính. Các dấu bằng cần được căn chỉnh thẳng hàng. Đối với các công thức phức tạp, việc sử dụng dấu ngoặc đơn, ngoặc vuông, ngoặc nhọn phải tuân theo thứ tự từ trong ra ngoài để tránh nhầm lẫn khi tính toán.

Công thức tổ hợp chỉnh hợp đóng vai trò quan trọng trong việc giải quyết các bài toán trong lĩnh vực toán học tổ hợp. Qua bài viết, bạn đã được tìm hiểu rõ ràng về các khái niệm hoán vị, chỉnh hợp và tổ hợp, cách áp dụng công thức một cách hiệu quả để giải quyết bài tập. Sự hiểu biết này sẽ giúp bạn tự tin hơn khi đối diện với các bài toán tổ hợp trong học tập.