Tập hợp là gì và các kiến thức cơ bản về tập hợp trong toán học

Tập hợp là gì? Đây là một khái niệm cơ bản trong toán học, giúp bạn hiểu cách phân loại và xử lý các yếu tố số học. Bài viết này sẽ giúp bạn khám phá định nghĩa, các loại tập hợp số, cũng như các phép toán và tính chất quan trọng liên quan. Hãy cùng tìm hiểu để nắm vững kiến thức và ứng dụng trong học tập!

Tập hợp là gì?

Tập hợp là gì là một khái niệm cơ bản trong toán học, dùng để chỉ một nhóm các phần tử có cùng một đặc điểm hoặc tính chất nào đó. Mỗi tập hợp được xác định bởi các phần tử riêng biệt và không lặp lại, được biểu diễn bằng cách liệt kê các phần tử trong cặp ngoặc nhọn.

Trong toán học, tập hợp được coi là nền tảng để xây dựng các cấu trúc toán học phức tạp hơn. Một tập hợp có thể chứa các phần tử là số, chữ cái, hình học, hoặc thậm chí là các tập hợp khác. Ví dụ, tập hợp các số tự nhiên từ 1 đến 5 được viết là {1, 2, 3, 4, 5}, hoặc tập hợp các nguyên âm trong tiếng Việt là {a, ă, â, e, ê, i, o, ô, ơ, u, ư}.

Tập hợp có thể là hữu hạn hoặc vô hạn. Tập hợp hữu hạn có số phần tử xác định và đếm được, trong khi tập hợp vô hạn có vô số phần tử. Ví dụ như tập hợp số tự nhiên N = {1, 2, 3,…} là một tập hợp vô hạn, còn tập hợp các tháng trong năm {1, 2, 3,…, 12} là tập hợp hữu hạn với 12 phần tử.

Các khái niệm cơ bản về tập hợp trong toán học

Trong Đại số, tập hợp toán học là một trong những khái niệm nền tảng quan trọng nhất. Tập hợp giúp chúng ta phân loại và tổ chức các đối tượng toán học một cách có hệ thống, từ đó xây dựng nên các lý thuyết phức tạp hơn.

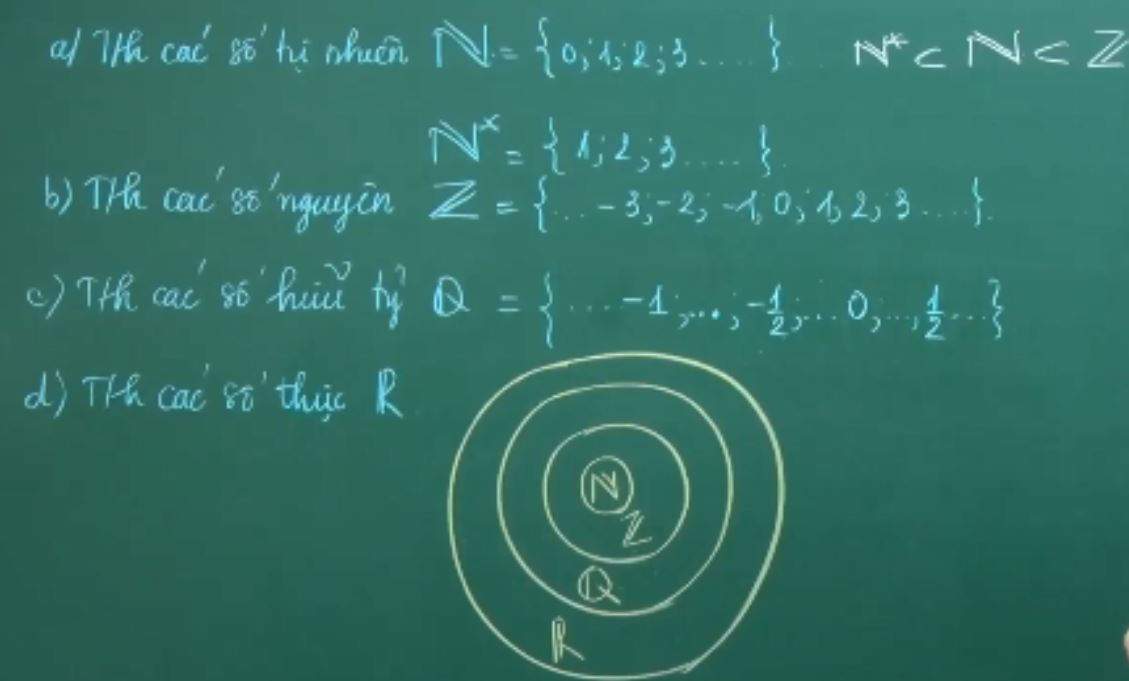
Định nghĩa và đặc điểm của tập hợp

Tập hợp là gì? Đó là một nhóm các phần tử có cùng một tính chất xác định nào đó. Mỗi phần tử trong tập hợp phải thỏa mãn hai điều kiện cơ bản: tính xác định và tính phân biệt.

Tính xác định nghĩa là có thể xác định rõ ràng một đối tượng có thuộc tập hợp hay không. Ví dụ, tập hợp các số tự nhiên chẵn nhỏ hơn 10 là một tập hợp xác định rõ ràng gồm các số 2, 4, 6, 8.

Tính phân biệt có nghĩa là mỗi phần tử trong tập hợp phải khác biệt với các phần tử còn lại. Không thể có hai phần tử giống hệt nhau trong cùng một tập hợp.

Phân loại các tập hợp số cơ bản

Định nghĩa tập hợp trong toán học được phân chia thành nhiều loại khác nhau. Tập hợp số tự nhiên N bao gồm các số nguyên không âm, bắt đầu từ 0. Tập hợp số nguyên Z mở rộng thêm các số âm vào tập số tự nhiên.

Tập hợp số hữu tỷ Q bao gồm các số có thể biểu diễn dưới dạng phân số a/b, với a và b là số nguyên và b khác 0. Tập hợp số thực R là tập hợp rộng nhất, bao gồm cả các số vô tỷ như π, √2.

Ngoài ra còn có các tập hợp đặc biệt như tập hợp rỗng (không có phần tử nào) và tập hợp hữu hạn (có số phần tử xác định).

Cách biểu diễn tập hợp và ký hiệu toán học

Kí hiệu tập hợp thường được biểu diễn bằng nhiều cách khác nhau. Phương pháp liệt kê trực tiếp là cách đơn giản nhất, liệt kê tất cả các phần tử trong dấu ngoặc nhọn. Ví dụ: A = {1, 2, 3, 4, 5}.

Phương pháp mô tả bằng tính chất sử dụng các biểu thức logic để xác định điều kiện của các phần tử. Ví dụ: B = {x | x là số nguyên dương nhỏ hơn 6}.

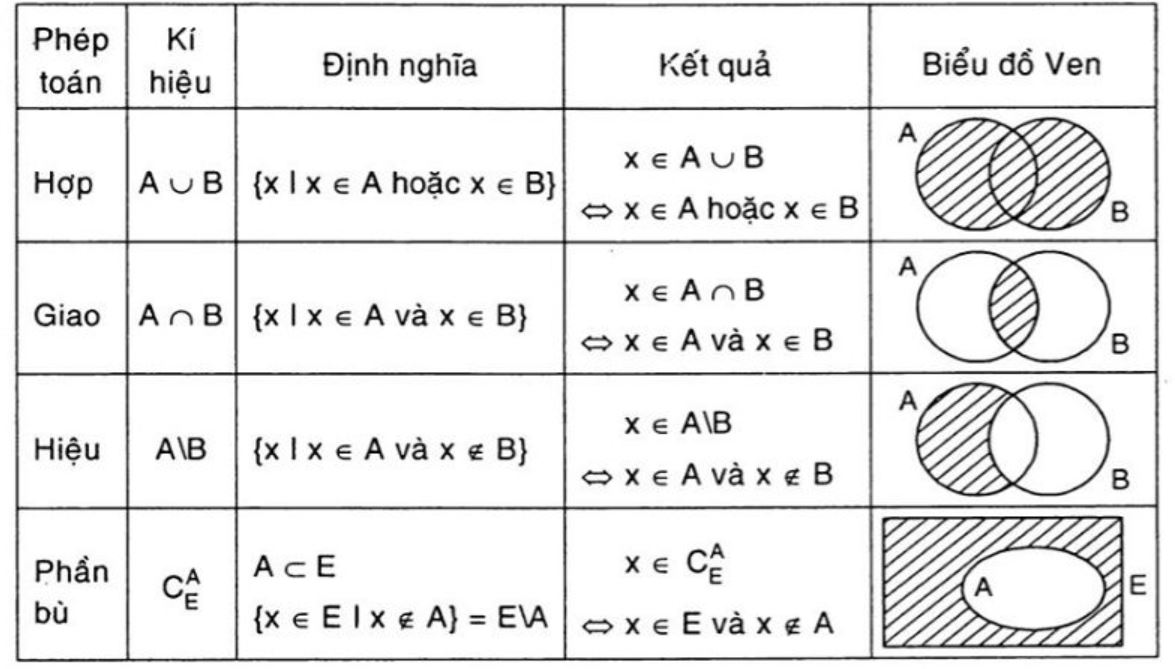
Biểu diễn bằng sơ đồ Venn là cách trực quan để thể hiện mối quan hệ giữa các tập hợp, đặc biệt hữu ích khi nghiên cứu các phép toán tập hợp như giao, hợp và hiệu của các tập hợp.

Các phép toán và tính chất của tập hợp

Các phép toán trên tập hợp là những quy tắc cơ bản để thực hiện các phép biến đổi và kết hợp giữa các tập hợp với nhau. Việc nắm vững các phép toán này giúp giải quyết nhiều bài toán trong toán học và ứng dụng thực tế.

Tập hợp là gì có thể hiểu đơn giản là một nhóm các phần tử có cùng một tính chất nào đó. Mỗi tập hợp được xác định bởi các phần tử riêng biệt và có thể thực hiện các phép toán khác nhau trên chúng. Các tính chất tập hợp quan trọng bao gồm tính giao hoán, kết hợp và phân phối.

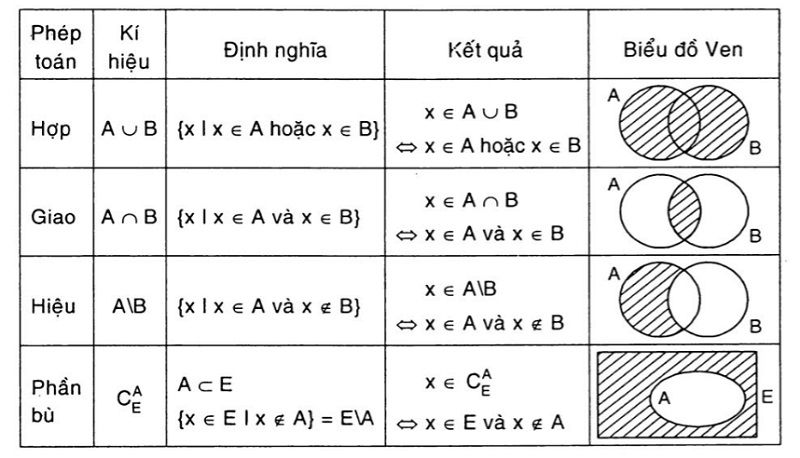
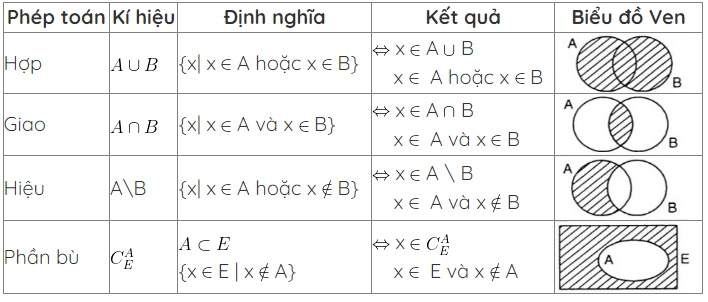
Phép hợp và giao của tập hợp

Phép hợp của hai tập hợp A và B (ký hiệu A ∪ B) là tập hợp gồm tất cả các phần tử thuộc A hoặc thuộc B. Ví dụ: A = {1,2,3}, B = {2,3,4} thì A ∪ B = {1,2,3,4}.

Phép giao của hai tập hợp A và B (ký hiệu A ∩ B) là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B. Với ví dụ trên, A ∩ B = {2,3}.

Phép hiệu và phép bù của tập hợp

Phép hiệu của hai tập A và B (ký hiệu A B) là tập hợp gồm các phần tử thuộc A nhưng không thuộc B. Phép hiệu thường được áp dụng trong phân loại dữ liệu và xử lý thông tin.

Phép bù của tập hợp A đối với tập vũ trụ U (ký hiệu A’) là tập hợp gồm các phần tử thuộc U nhưng không thuộc A. Phép bù giúp xác định những phần tử còn lại trong không gian mẫu.

Tích Đề-các của hai tập hợp

Định nghĩa và ví dụ minh họa

Tích Đề-các của hai tập A và B (ký hiệu A × B) là tập hợp gồm tất cả các cặp có thứ tự (a,b) trong đó a thuộc A và b thuộc B. Ví dụ: A = {1,2}, B = {x,y} thì A × B = {(1,x), (1,y), (2,x), (2,y)}.

Tích Đề-các có tính chất không giao hoán, nghĩa là A × B ≠ B × A. Điều này tạo nên sự khác biệt quan trọng so với các phép toán tập hợp khác.

Ứng dụng trong bài toán thực tế

Tích Đề-các được ứng dụng rộng rãi trong nhiều lĩnh vực như lập trình, cơ sở dữ liệu và thống kê. Theo nghiên cứu của Đại học Stanford, tích Đề-các giúp mô hình hóa các mối quan hệ trong cơ sở dữ liệu quan hệ.

Trong lĩnh vực logistics, các công ty vận tải sử dụng tích Đề-các để tối ưu hóa lộ trình vận chuyển. Ví dụ, công ty DHL áp dụng nguyên lý này để tính toán tất cả các cặp điểm xuất phát – điểm đến có thể có.

Tập hợp con và mối quan hệ giữa các tập hợp

Khi nghiên cứu về các tập hợp, việc hiểu rõ mối quan hệ giữa chúng là vô cùng quan trọng. Mối quan hệ này thể hiện qua khái niệm tập hợp con, quan hệ bao hàm và tính chất bằng nhau giữa các tập hợp.

Khái niệm tập hợp con

Tập hợp con là gì? Một tập hợp A được gọi là tập hợp con của tập hợp B nếu mọi phần tử của A đều thuộc B. Ví dụ như tập hợp số chẵn dương là tập hợp con của tập hợp số tự nhiên.

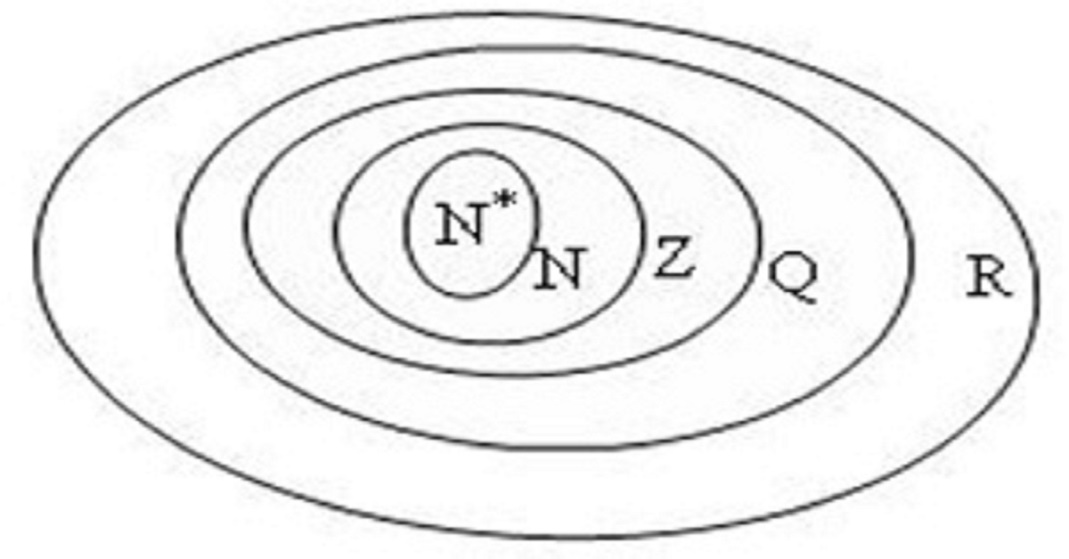
Trong toán học, r là tập hợp số gì thường được đề cập khi nghiên cứu về mối quan hệ giữa các tập số. Tập hợp số thực R có nhiều tập hợp con quan trọng như tập số hữu tỷ Q hay tập số nguyên Z.

Quan hệ bao hàm giữa các tập hợp

Quan hệ bao hàm là mối quan hệ cơ bản giữa hai tập hợp, được ký hiệu bằng dấu ⊂. Khi tập A là tập con của tập B, ta viết A ⊂ B.

Quan hệ bao hàm có tính chất phản xạ (mọi tập hợp đều là tập con của chính nó) và tính chất bắc cầu (nếu A ⊂ B và B ⊂ C thì A ⊂ C). Những tính chất này giúp ta sắp xếp và phân loại các tập hợp một cách logic.

Tập hợp bằng nhau và tập hợp tương đương

Hai tập hợp được gọi là bằng nhau khi chúng có cùng các phần tử. Điều này có nghĩa là mỗi phần tử của tập hợp này đều thuộc tập hợp kia và ngược lại.

Khái niệm tập hợp tương đương lại khác với tập hợp bằng nhau. Hai tập hợp được gọi là tương đương khi chúng có cùng số phần tử, nhưng các phần tử có thể khác nhau. Tập hợp là gì sẽ được hiểu rõ hơn khi ta nắm vững các mối quan hệ này.

Trong thực tế, việc phân biệt giữa tập hợp bằng nhau và tương đương rất quan trọng, đặc biệt trong các bài toán về xác suất thống kê và lý thuyết tổ hợp.

Các dạng tập hợp số quan trọng trong toán học

Các tập hợp số là những khái niệm nền tảng trong toán học, giúp phân loại và tổ chức các con số theo những tính chất đặc trưng. Việc hiểu rõ về tập hợp là gì và các loại tập hợp sẽ giúp người học nắm vững kiến thức toán học cơ bản.

Mỗi tập hợp số có những đặc điểm và phạm vi ứng dụng riêng, từ đơn giản đến phức tạp. Chúng được sắp xếp theo thứ tự mở rộng dần, bắt đầu từ tập hợp số tự nhiên, số nguyên, số hữu tỉ và cuối cùng là số thực.

Tập hợp số tự nhiên (N)

Tập hợp số tự nhiên bao gồm các số nguyên dương từ 1 trở đi và số 0. Đây là tập hợp đầu tiên con người tiếp xúc và sử dụng trong cuộc sống hàng ngày.

Tập N có tính chất đặc biệt là mỗi số tự nhiên đều có số liền sau, nhưng không phải số nào cũng có số liền trước (như số 0). Tập hợp này được sử dụng phổ biến trong đếm số và tính toán cơ bản.

Tập hợp số nguyên (Z)

Tập hợp số nguyên mở rộng từ tập số tự nhiên bằng cách bổ sung thêm các số âm. Nó bao gồm tất cả các số nguyên âm, số 0 và các số nguyên dương.

Trong thực tế, tập Z thường được áp dụng để biểu diễn các đại lượng có thể âm hoặc dương như nhiệt độ, độ cao so với mực nước biển. Tập hợp này đóng vai trò quan trọng trong đại số và lý thuyết số.

Tập hợp số hữu tỉ (Q)

Tập hợp số hữu tỉ bao gồm các số có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là số nguyên, b khác 0. Đây là bước phát triển quan trọng giúp giải quyết nhiều bài toán thực tế.

Số hữu tỉ có thể viết dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn. Chúng được sử dụng rộng rãi trong đo lường chính xác và các phép tính phân số.

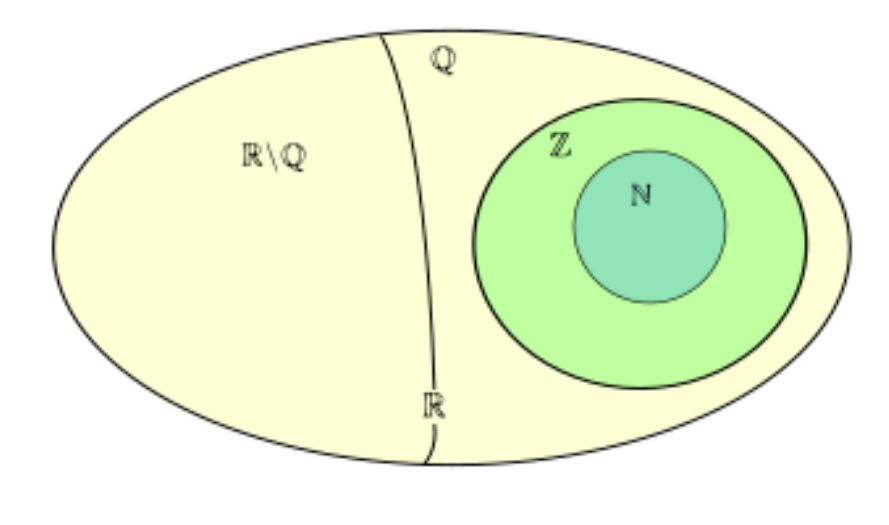
Tập hợp số thực (R)

Tập hợp số thực là tập hợp rộng nhất, bao gồm cả số hữu tỉ và số vô tỉ. Số vô tỉ là những số không thể biểu diễn dưới dạng phân số, như π hay √2.

Số thực có vai trò then chốt trong hình học, giải tích và nhiều lĩnh vực toán học cao cấp. Chúng cho phép biểu diễn mọi điểm trên trục số, tạo nên tính liên tục của đường thẳng số.

Bài tập và phương pháp giải về tập hợp

Việc nắm vững các bài tập tập hợp là nền tảng quan trọng để học tốt toán học. Phần này sẽ giới thiệu các dạng bài tập phổ biến cùng phương pháp giải chi tiết, giúp người học có thể áp dụng hiệu quả vào thực tế.

Các dạng bài tập thường gặp

Trong chương trình toán phổ thông, các ví dụ tập hợp thường xuất hiện dưới nhiều hình thức đa dạng. Bài tập về phép hợp, giao của các tập hợp là dạng cơ bản nhất. Tiếp đến là các bài toán về tính số phần tử của tập hợp, xác định quan hệ giữa các tập hợp.

Ngoài ra còn có các bài tập nâng cao như chứng minh tính chất của tập hợp, giải phương trình và bất phương trình với tập hợp nghiệm. Mỗi dạng bài đều có những đặc điểm và cách tiếp cận riêng cần được nắm vững.

Phương pháp giải và ví dụ minh họa

Để giải tốt bài tập về tập hợp, cần nắm chắc các phương pháp cơ bản. Đầu tiên là phương pháp liệt kê trực tiếp các phần tử, phù hợp với tập hợp hữu hạn. Với tập hợp vô hạn, ta sử dụng phương pháp mô tả bằng tính chất đặc trưng.

Các ứng dụng tập hợp trong thực tế rất đa dạng, từ việc phân loại dữ liệu đến tối ưu hóa quy trình. Ví dụ như trong ngành logistics, việc phân chia các đơn hàng thành các tập hợp theo khu vực giúp tối ưu tuyến đường vận chuyển.

Khi giải bài tập, cần vẽ sơ đồ Venn để biểu diễn trực quan mối quan hệ giữa các tập hợp. Điều này giúp hình dung rõ ràng và tránh nhầm lẫn khi thực hiện các phép toán.

Bài tập tự luyện có lời giải

Bài tập 1: Cho A = {x ∈ N | x < 10}, B = {x ∈ N | x là số chẵn và x ≤ 8}. Tìm A∩B và A∪B.

Lời giải:
A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {2, 4, 6, 8}
A∩B = {2, 4, 6, 8}
A∪B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Bài tập 2: Cho tập hợp M = {x ∈ R | -2 ≤ x ≤ 5}. Biểu diễn M trên trục số và viết M dưới dạng khoảng.

Lời giải:
M = [-2,5]
Biểu diễn trên trục số: Đoạn thẳng từ -2 đến 5 bao gồm cả 2 điểm đầu mút.

Khi tìm hiểu về tập hợp là gì, bạn sẽ khám phá các khái niệm cơ bản như định nghĩa tập hợp, các loại tập hợp số và các phép toán trên tập hợp. Nắm vững những điểm này không chỉ giúp bạn giải quyết bài tập toán mà còn áp dụng linh hoạt vào thực tế cuộc sống. Sự đa dạng và phong phú của tập hợp sẽ mở ra nhiều cơ hội học tập mới dành cho bạn trong hành trình chinh phục môn toán.