Hướng dẫn tính đạo hàm hàm hợp f(g(x) với quy tắc và công thức cơ bản

Đạo hàm hàm hợp là phần quan trọng trong toán học, đặc biệt trong giải tích. Các quy tắc và công thức tính toán liên quan đến hàm số dạng f(g(x)) giúp giải quyết nhiều bài toán phức tạp. Hãy khám phá quy trình, công thức và các ứng dụng cụ thể để nâng cao kỹ năng giải toán của bạn.

Đạo hàm hàm hợp là phép tính đạo hàm của hàm số dạng f(g(x))

Đạo hàm hàm hợp là một phương pháp tính đạo hàm quan trọng trong giải tích, áp dụng cho các hàm số có dạng phức hợp f(g(x)). Phương pháp này giúp tính đạo hàm của hàm hợp thông qua quy tắc nhân đạo hàm của hàm bên ngoài với đạo hàm của hàm bên trong.

Khi áp dụng đạo hàm của hàm hợp, ta cần xác định rõ hàm bên ngoài f(x) và hàm bên trong g(x). Ví dụ với hàm trùng phương, ta có thể viết dưới dạng hàm hợp f(g(x)) = (g(x))² với g(x) = x². Việc tính đạo hàm sẽ được thực hiện theo từng bước, từ ngoài vào trong.

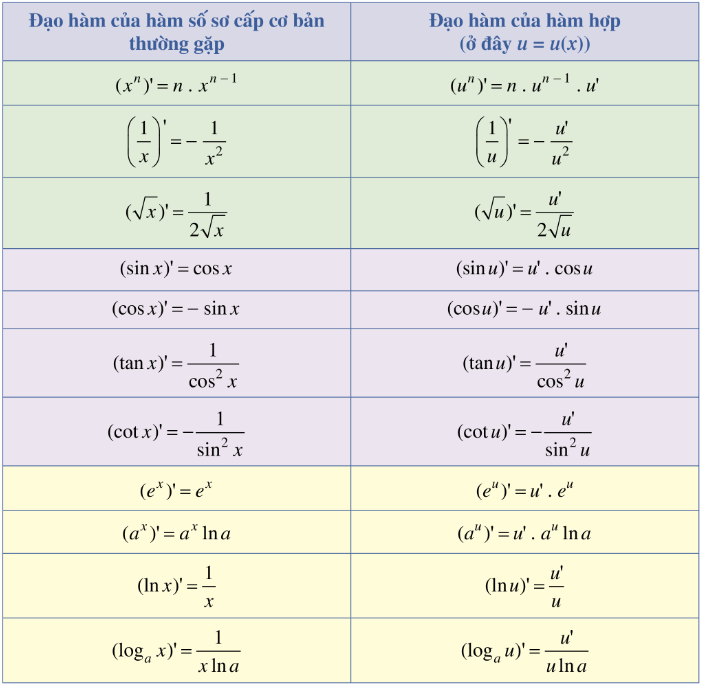
Công thức tổng quát cho đạo hàm hàm hợp là: [f(g(x))]’ = f'(g(x)) × g'(x). Trong đó f'(g(x)) là đạo hàm của hàm ngoài tính tại g(x), và g'(x) là đạo hàm của hàm trong. Việc nắm vững công thức này giúp giải quyết nhiều bài toán phức tạp trong toán học và ứng dụng thực tế.

Quy tắc tính đạo hàm hàm hợp và công thức cơ bản

Quy tắc đạo hàm là một trong những kiến thức nền tảng quan trọng trong giải tích. Khi áp dụng vào hàm hợp, ta cần nắm vững công thức và các bước thực hiện cụ thể để tính toán chính xác.

Để tính đạo hàm của các hàm phức tạp, việc nắm vững bảng đạo hàm đầy đủ là điều cần thiết. Tuy nhiên, với đạo hàm hàm hợp f(g(x)), ta cần áp dụng thêm các quy tắc đặc biệt.

Công thức tổng quát đạo hàm hàm hợp f(g(x))

Công thức đạo hàm hàm hợp có dạng: [f(g(x))]’ = f'(g(x)) × g'(x). Trong đó, f'(g(x)) là đạo hàm của hàm f tính tại g(x), và g'(x) là đạo hàm của hàm g tại x.

Công thức này được phát triển bởi Gottfried Wilhelm Leibniz vào thế kỷ 17 và đã trở thành một trong những công cụ quan trọng trong phép tính vi phân. Việc áp dụng đúng công thức sẽ giúp giải quyết nhiều bài toán phức tạp.

Các bước tính đạo hàm hàm hợp

Để tính đạo hàm hàm hợp một cách chính xác và hiệu quả, ta cần thực hiện theo trình tự các bước logic. Mỗi bước đều đóng vai trò quan trọng trong việc đảm bảo kết quả cuối cùng chính xác.

Xác định hàm f(u) và u = g(x)

Bước đầu tiên là phân tích hàm số thành dạng hàm hợp bằng cách xác định hàm bên trong và hàm bên ngoài. Điều này giúp ta thấy rõ cấu trúc của hàm số và áp dụng công thức một cách chính xác.

Ví dụ với hàm y = sin(x²), ta có thể viết lại dưới dạng f(u) = sin(u) và u = x². Việc phân tích này giúp việc tính toán trở nên rõ ràng và có hệ thống hơn.

Áp dụng công thức đạo hàm hàm hợp

Sau khi đã xác định được các thành phần, ta áp dụng công thức đạo hàm hàm hợp theo trình tự:

• Tính đạo hàm của hàm bên ngoài f'(u)
• Tính đạo hàm của hàm bên trong g'(x)
• Nhân hai kết quả với nhau

Quá trình này cần được thực hiện cẩn thận và kiểm tra lại từng bước để tránh sai sót. Việc ghi chép các bước tính toán một cách rõ ràng sẽ giúp dễ dàng phát hiện và sửa lỗi nếu có.

Các trường hợp đặc biệt khi tính đạo hàm hàm hợp f(u)

Khi tính đạo hàm f(u), ta cần lưu ý một số trường hợp đặc biệt để áp dụng công thức cho phù hợp. Việc nắm vững các quy tắc tính đạo hàm của f(u) sẽ giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả.

Trong quá trình tính toán, f(u) đạo hàm thường xuất hiện dưới dạng các hàm số quen thuộc như lượng giác, mũ logarit và đa thức. Mỗi dạng hàm số sẽ có những đặc điểm riêng và cách tính đạo hàm khác nhau.

Đạo hàm hàm hợp với hàm lượng giác

Với các hàm lượng giác, việc tính đạo hàm cần tuân theo các công thức cơ bản và quy tắc đạo hàm hàm hợp. Ví dụ khi tính đạo hàm của sin(2x), ta cần áp dụng quy tắc hàm hợp với u = 2x.

Ngoài các hàm lượng giác cơ bản, ta còn gặp các hàm lượng giác ngược như đạo hàm arcsin u. Đây là những trường hợp đặc biệt cần áp dụng đạo hàm hàm ngược kết hợp với quy tắc hàm hợp.

Đạo hàm hàm hợp với hàm mũ và logarit

Khi tính đạo hàm của hàm mũ dạng ax, ta luôn có hệ số là ln(a). Điều này xuất phát từ bản chất của hàm mũ và logarit tự nhiên. Với hàm eu, đạo hàm sẽ cho kết quả chính là eu.

Đối với hàm logarit, đạo hàm của ln(u) là 1/u. Từ đó ta có thể suy ra công thức đạo hàm của loga(u) thông qua công thức đổi cơ số logarit. Việc nắm vững các công thức này giúp giải quyết nhiều bài toán phức tạp.

Đạo hàm hàm hợp với hàm đa thức

Đạo hàm của hàm đa thức tuân theo quy tắc giảm số mũ và nhân với số mũ. Khi gặp hàm hợp dạng [f(u)]n, ta cần áp dụng quy tắc hàm hợp kết hợp với quy tắc lũy thừa.

Trong thực tế, các hàm đa thức thường xuất hiện dưới dạng tích của nhiều thừa số. Khi đó, ta cần kết hợp quy tắc nhân và quy tắc hàm hợp để tính đạo hàm. Việc phân tích hàm số thành các thành phần đơn giản sẽ giúp quá trình tính toán trở nên dễ dàng hơn.

Ví dụ minh họa và bài tập áp dụng đạo hàm hàm hợp

Việc áp dụng đạo hàm hàm hợp đòi hỏi sự thành thạo trong việc nhận dạng dạng hàm và vận dụng các quy tắc một cách linh hoạt. Tương tự như cách chúng ta làm việc với các tập hợp số​, việc phân tích cấu trúc hàm hợp giúp quá trình tính đạo hàm trở nên có hệ thống hơn.

Khi giải các bài toán về các quy tắc tính đạo hàm, việc nắm vững phương pháp và thực hành nhiều sẽ giúp phát triển kỹ năng tính toán nhanh chóng và chính xác. Giống như cách chúng ta nghiên cứu về khối đa diện, mỗi dạng bài tập đều có những đặc điểm riêng cần được phân tích kỹ lưỡng.

Các dạng bài tập thường gặp

Trong quá trình học tập và ôn luyện về đạo hàm hợp, có nhiều dạng bài tập khác nhau đòi hỏi các phương pháp giải quyết riêng biệt. Một số dạng phổ biến bao gồm tìm đạo hàm của hàm số phức hợp, xác định tiếp tuyến của đồ thị hàm số, và tính giá trị đạo hàm tại một điểm.

Việc phân loại và nắm vững đặc điểm của từng dạng bài tập sẽ giúp người học xây dựng chiến lược giải quyết hiệu quả. Mỗi dạng bài tập đều có những “mẹo” riêng trong cách áp dụng công thức và quy tắc.

Phương pháp giải và lời giải chi tiết

Để giải các bài tập về đạo hàm hàm hợp, cần tuân theo quy trình giải có hệ thống. Bước đầu tiên là nhận dạng dạng hàm số, tiếp đến là xác định các hàm thành phần và cuối cùng là áp dụng quy tắc tính đạo hàm phù hợp.

Việc trình bày lời giải cần rõ ràng, logic và đầy đủ các bước tính toán. Điều này không chỉ giúp kiểm tra lại kết quả mà còn hỗ trợ việc học tập và ghi nhớ phương pháp giải.

Bài tập về đạo hàm hàm số lượng giác

Khi giải bài tập về đạo hàm hàm số lượng giác, việc nắm vững các công thức đạo hàm cơ bản của hàm sin, cos, tan, cotg là vô cùng quan trọng. Các bài tập thường yêu cầu kết hợp nhiều kỹ năng như phân tích hàm hợp và áp dụng các công thức lượng giác.

Một số bài tập đòi hỏi khả năng biến đổi phức tạp, đặc biệt khi gặp các hàm số dạng tích hoặc thương của các hàm lượng giác. Việc rèn luyện thường xuyên sẽ giúp phát triển trực giác toán học và kỹ năng tính toán.

Bài tập về đạo hàm hàm mũ và logarit

Đối với đạo hàm hàm mũ và logarit, các bài tập thường tập trung vào việc vận dụng các tính chất đặc trưng của hàm số. Việc hiểu r

Các sai lầm thường gặp khi tính đạo hàm hàm hợp và cách khắc phục

Việc tính đạo hàm hàm hợp thường gặp nhiều khó khăn do tính phức tạp trong cấu trúc của hàm số. Nhiều học sinh và sinh viên mắc phải những sai lầm cơ bản khi áp dụng quy tắc tính đạo hàm, dẫn đến kết quả không chính xác.

Để tránh những sai sót này, việc nắm vững nguyên tắc và thực hành thường xuyên là rất quan trọng. Đặc biệt cần chú ý đến công thức hàm hợp và các bước áp dụng một cách có hệ thống.

Nhầm lẫn giữa các quy tắc đạo hàm

Một trong những sai lầm phổ biến nhất là việc áp dụng nhầm quy tắc đạo hàm cho từng dạng hàm số. Ví dụ khi gặp hàm y = sin(x²), nhiều người vội vàng áp dụng công thức đạo hàm của hàm sin mà quên mất phần biến đổi bên trong.

Để tránh nhầm lẫn, cần phân tích kỹ cấu trúc của hàm số trước khi tính toán. Việc xác định đúng hàm bên trong và hàm bên ngoài sẽ giúp áp dụng chính xác quy tắc tính đạo hàm hàm hợp.

Theo GS. Nguyễn Văn A – Đại học Sư phạm Hà Nội, sinh viên thường mắc lỗi khi gặp các hàm phức tạp như logarit hay lũy thừa của hàm lượng giác. Cần có phương pháp tiếp cận có hệ thống và kiểm tra kỹ kết quả.

Cách nhận biết và tránh các lỗi phổ biến

Việc nhận biết các dạng bài tập thường gặp sẽ giúp tránh được những sai lầm cơ bản. Khi gặp hàm số phức tạp, nên chia nhỏ thành các phần đơn giản hơn để dễ dàng xử lý.

Một số lưu ý quan trọng khi tính đạo hàm:

• Xác định rõ hàm bên trong và hàm bên ngoài
• Áp dụng đúng thứ tự các quy tắc tính đạo hàm
• Kiểm tra lại kết quả bằng cách thế các giá trị cụ thể

Ngoài ra, việc thực hành nhiều bài tập đa dạng sẽ giúp rèn luyện kỹ năng và tránh được những sai sót thường gặp. Theo thống kê của Khoa Toán – Đại học Khoa học Tự nhiên, sinh viên thường mắc lỗi nhiều nhất trong 2 tháng đầu học phần Giải tích, sau đó tỷ lệ sai sót giảm đáng kể nhờ việc luyện tập thường xuyên.

Trong việc học toán, đạo hàm hàm hợp đóng vai trò quan trọng giúp giải quyết nhiều bài toán phức tạp. Bài viết đã trình bày quy tắc tính đạo hàm cơ bản, các trường hợp đặc biệt và những sai lầm thường gặp, qua đó giúp người đọc nắm vững và áp dụng hiệu quả các công thức cần thiết. Hãy tiếp tục rèn luyện để củng cố kiến thức của mình một cách chắc chắn.